吴恩达机器学习笔记（七） —— K-means算法

主要内容：

一.K-means算法简介

二.算法过程

三.随机初始化

四.二分K-means

四.K的选择

一.K-means算法简介

1.K-means算法是一种无监督学习算法。所谓无监督式学习，就是输入样本中只有x，没有y，即只有特征，而没有标签，通过这些特征对数据进行整合等操作。而更细化一点地说，K-means算法属于聚类算法。所谓聚类算法，就是根据特征上的相似性，把数据聚集在一起，或者说分成几类。

2.K-means算法作为聚类算法的一种，其工作自然也是“将数据分成几类”，其基本思路是：

1) 首先选择好将数据分成k类，然后随机初始化k个点作为中心点。

2) 对于每一个数据点，选取与之距离最近的中心点作为自己的类别。

3) 当所有数据点都归类完毕后，调整中心点：把中心点重新设置为该类别中所有数据点的中心位置，每一轴都设置为平均值。（所以称为means）

4) 重复以上2)~3)步骤直至数据点的类别不再发生变化。

3.K-means算法从感性上去理解，就是把一堆靠得近的点归到同一个类别中。

二.算法过程

1.一些变量的约定：μ(i)表示第i个中心点，c(i)表示第i个数据点归到哪个中心点。

2.K-means算法的本质就是：移动中心点，使其渐渐地靠近数据的“中心”，即最小化数据点与中心点的距离。即：

3.算法流程：

4.Python代码如下：

 # coding:utf-8
 
 from numpy import *
 
 def distEclud(vecA, vecB):      #计算欧式距离
     return sqrt(sum(power(vecA - vecB, 2)))  # la.norm(vecA-vecB)
 
 def randCent(dataSet, k):         #  初始化k个随机簇心
     n = shape(dataSet)[1]       #特征个数
     centroids = mat(zeros((k, n)))  # 簇心矩阵k*n
     for j in range(n):  #特征逐个逐个地分配给这k个簇心。每个特征的取值需要设置在数据集的范围内
         minJ = min(dataSet[:, j])   #数据集中该特征的最小值
         rangeJ = float(max(dataSet[:, j]) - minJ)   #数据集中该特征的跨度
         centroids[:, j] = mat(minJ + rangeJ * random.rand(k, 1))    #为k个簇心分配第j个特征，范围需限定在数据集内。
     return centroids        #返回k个簇心
 
 def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
     m = shape(dataSet)[0]    #数据个数
     clusterAssment = mat(zeros((m, 2)))  # 记录每个数据点被分配到的簇，以及到簇心的距离
     centroids = createCent(dataSet, k)      #  初始化k个随机簇心
     clusterChanged = True       #  记录一轮中是否有数据点的归属出现变化，如果没有则算法结束
     while clusterChanged:
         clusterChanged = False
         for i in range(m):  # 枚举每个数据点，重新分配其簇归属
             minDist = inf; minIndex = -1    #记录最近簇心及其距离
             for j in range(k):      #枚举每个簇心
                 distJI = distMeas(centroids[j, :], dataSet[i, :])   #计算数据点与簇心的距离
                 if distJI < minDist:        #更新最近簇心
                     minDist = distJI;  minIndex = j
             if clusterAssment[i, 0] != minIndex: clusterChanged = True  #更新“变化”记录
             clusterAssment[i, :] = minIndex, minDist ** 2     #更新数据点的簇归属
         print centroids
         for cent in range(k):  #枚举每个簇心，更新其位置
             ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]]  # 得到该簇所有的数据点
             centroids[cent, :] = mean(ptsInClust, axis=0)  # 将数据点的均值作为簇心的位置
     return centroids, clusterAssment    # 返回簇心及每个数据点的簇归属

三.随机初始化

由于初始化的中心点对于最后的分类结果影响很大，因而很容易出现：当初始化的中心点不同时，其结果可能千差万别：

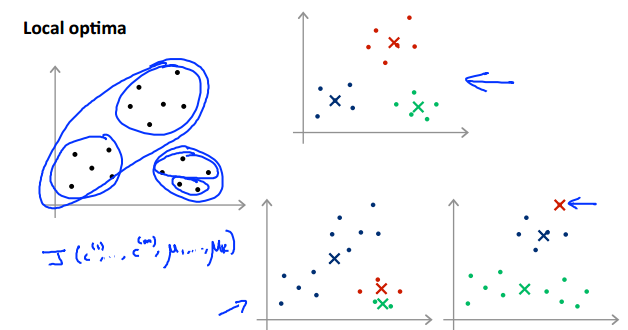
因此，为了分类结果更加合理，我们可以多次初始化中心点，即多次运行K-means算法，然后取其中J(c1,c2……，μ1,μ2……)最小的分类结果。

四.二分K-means

1.为了克服K-means算法收敛域局部最小值的问题（缘因对初始簇心的位置敏感），二分k-means出现了。该算法首先将所有点归于一个簇，然后将其一分为二。之后选择其中一个簇继续一分为二。选择的依据就是：该簇的划分是否可以最大程度降低SSE（误差平方和）的值。上述基于SSE的划分过程不断重复，直至簇数达到k为止。

2.伪代码如下：

3.Python代码如下：

 '''二分K均值'''
 def biKmeans(dataSet, k, distMeas=distEclud):
     m = shape(dataSet)[0]
     centroid0 = mean(dataSet, axis=0).tolist()[0]   #创建初始簇心，标号为0
     centList = [centroid0]  # 创建簇心列表
     clusterAssment = mat(zeros((m, 2)))     #初始化所有数据点的簇归属(为0)
     for j in range(m):  # 计算所有数据点与簇心0的距离
         clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :]) ** 2
     ''''''''''''
     while (len(centList) < k):      #分裂k-1次，形成k个簇
         lowestSSE = inf     #初始化最小sse为无限大
         for i in range(len(centList)):      #枚举已有的簇，尝试将其一分为二
             ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0],:]  #将该簇的数据点提取出来
             centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)  #利用普通k均值将其一分为二
             sseSplit = sum(splitClustAss[:, 1])  # 计算划分后该簇的SSE
             sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])   #计算该簇之外的数据点的SSE
             print "sseSplit, and notSplit: ", sseSplit, sseNotSplit
             if (sseSplit + sseNotSplit) < lowestSSE:    #更新最小总SSE下的划分簇及相关信息
                 bestCentToSplit = i         #被划分的簇
                 bestNewCents = centroidMat      #划分后的两个簇心
                 bestClustAss = splitClustAss.copy()         #划分后簇内数据点的归属及到新簇心的距离
                 lowestSSE = sseSplit + sseNotSplit      #更新最小总SSE
         ''''''''''''
         print 'the bestCentToSplit is: ', bestCentToSplit
         print 'the len of bestClustAss is: ', len(bestClustAss)
         centList[bestCentToSplit] = bestNewCents[0, :].tolist()[0]  # 一个新簇心的标号为旧簇心的标号，所以将其取代就簇心的位置
         centList.append(bestNewCents[1, :].tolist()[0])     # 另一个新簇心加入到簇心列表的尾部，标号重新起
         bestClustAss[nonzero(bestClustAss[:, 0].A == 1)[0], 0] = len(centList)      #更新旧簇内数据点的标号
         bestClustAss[nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit    #同上
         clusterAssment[nonzero(clusterAssment[:, 0].A == bestCentToSplit)[0],:] = bestClustAss  # 将更新的簇归属统计到总数据上
     return mat(centList), clusterAssment

四.K的选择

最后一个问题：既然是K-means，那么这个k应该取多大呢？

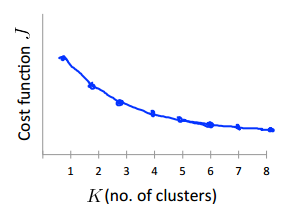
一.Elbow method：

假设随着k的增大，cost function j的大小呈现以下的形状：

可以看到，当k=3时，J已经很小了，且再增大k也不能大大地减小J。说明此时k选取3比较合适。

但是，这种“手肘”情况并不常见，更一般的情况是：

此时根本看不出哪里才是“手肘”，所以对此的策略是：实践调研，按实际需求的而定。