POJ3415 Common Substrings —— 后缀数组 + 单调栈 公共子串个数

题目链接：https://vjudge.net/problem/POJ-3415

Common Substrings

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 12240		Accepted: 4144

Description

A substring of a string T is defined as:

T(i, k)=T_iT_i+1...T_i+k-1, 1≤i≤i+k-1≤|T|.

Given two strings A, B and one integer K, we define S, a set of triples (i, j, k):

S = {(i, j, k) | k≥K, A(i, k)=B(j, k)}.

You are to give the value of |S| for specific A, B and K.

Input

The input file contains several blocks of data. For each block, the first line contains one integer K, followed by two lines containing strings A and B, respectively. The input file is ended by K=0.

1 ≤ |A|, |B| ≤ 10⁵
1 ≤ K ≤ min{|A|, |B|}
Characters of A and B are all Latin letters.

Output

For each case, output an integer |S|.

Sample Input

2
aababaa
abaabaa
1
xx
xx
0

Sample Output

22
5

Source

POJ Monthly--2007.10.06, wintokk

题意：

给出两个字符串，求有多少对长度不小于k的公共子串，子串相同但位置不同也单独算作一对。

题解：

1.将两个字符串拼接在一起，中间用分隔符隔开，得到新串。并且需要记录每个位置上的字符（后缀）属于哪一个字符串。

2.求出新串的后缀数组。可知sa[i]和sa[j]的最长公共前缀为：min（height[k]）i+1<=k<=j。

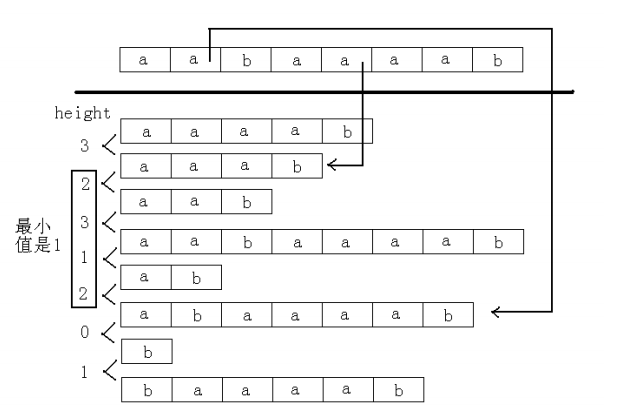
3.根据第二点，可以枚举sa数组，当遇到A串时，就先放着，当遇到B串时，就往前统计与所有A串的最长公共前缀，假如为len，那么就能增加len-k+1个公共前缀了。由于是按着sa的顺序枚举下去的，所以对于在B串下面的A串是没有统计到的，所以需要二次统计：把A串当成B串， B串当成A串，然后再进行统计，方可无遗漏。

4.往前统计时需要用到单调栈。

代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 const int MOD = 1e9+;
 const int MAXN = 2e5+;
 
 int id[MAXN];
 int r[MAXN], sa[MAXN], Rank[MAXN], height[MAXN];
 int t1[MAXN], t2[MAXN], c[MAXN];
 
 bool cmp(int *r, int a, int b, int l)
 {
     return r[a]==r[b] && r[a+l]==r[b+l];
 }
 
 void DA(int str[], int sa[], int Rank[], int height[], int n, int m)
 {
     n++;
     int i, j, p, *x = t1, *y = t2;
     for(i = ; i<m; i++) c[i] = ;
     for(i = ; i<n; i++) c[x[i] = str[i]]++;
     for(i = ; i<m; i++) c[i] += c[i-];
     for(i = n-; i>=; i--) sa[--c[x[i]]] = i;
     for(j = ; j<=n; j <<= )
     {
         p = ;
         for(i = n-j; i<n; i++) y[p++] = i;
         for(i = ; i<n; i++) if(sa[i]>=j) y[p++] = sa[i]-j;
 
         for(i = ; i<m; i++) c[i] = ;
         for(i = ; i<n; i++) c[x[y[i]]]++;
         for(i = ; i<m; i++) c[i] += c[i-];
         for(i = n-; i>=; i--) sa[--c[x[y[i]]]] = y[i];
 
         swap(x, y);
         p = ; x[sa[]] = ;
         for(i = ; i<n; i++)
             x[sa[i]] = cmp(y, sa[i-], sa[i], j)?p-:p++;
 
         if(p>=n) break;
         m = p;
     }
 
     int k = ;
     n--;
     for(i = ; i<=n; i++) Rank[sa[i]] = i;
     for(i = ; i<n; i++)
     {
         if(k) k--;
         j = sa[Rank[i]-];
         while(str[i+k]==str[j+k]) k++;
         height[Rank[i]] = k;
     }
 }
 
 int Stack[MAXN][], top;
 LL cal(int k, int len, int flag)
 {
     LL sum = , tmp = ;
     top = ;
     for(int i = ; i<=len; i++)
     {
         if(height[i]<k)
             tmp = top = ;
         else
         {
             int cnt = ;
             if(id[sa[i-]]==flag)
                 tmp += height[i]-k+, cnt++;
             while(top> && height[i]<=Stack[top-][])
             {
                 tmp -= 1LL*Stack[top-][]*(Stack[top-][]-height[i]);
                 cnt += Stack[top-][];
                 top--;
             }
             Stack[top][] = height[i];
             Stack[top++][] = cnt;
             if(id[sa[i]]!=flag)
                 sum += tmp;
         }
     }
     return sum;
 }
 
 char str[MAXN];
 int main()
 {
     int k;
     while(scanf("%d",&k)&&k)
     {
         int len = ;
         scanf("%s", str);
         int LEN = strlen(str);
         for(int j = ; j<LEN; j++)
         {
             r[len] = str[j];
             id[len++] = ;
         }
         r[len] = '$';
         id[len++] = ;
         scanf("%s", str);
         LEN = strlen(str);
         for(int j = ; j<LEN; j++)
         {
             r[len] = str[j];
             id[len++] = ;
         }
         r[len] = ;
         DA(r,sa,Rank,height,len,);
         cout<< cal(k,len,)+cal(k,len,) <<endl;
     }
 }