二叉搜索树详解（Java实现）
二叉搜索树定义
二叉搜索树，是指一棵空树或者具有下列性质的二叉树：
- 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
- 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
- 任意节点的左，右子树也分别为二叉搜索树；
- 没有键值相等的节点。
用Java来表示二叉树
public class BinarySearchTree
{ // 二叉搜索树类
private class Node
{ // 节点类
int data; // 数据域
Node right; // 右子树
Node left; // 左子树
} private Node root; // 树根节点
}
首先，需要一个节点对象的类。这个对象包含数据域和指向节点的两个子节点的引用。
其次，需要一个树对象的类。这个对象包含一个根节点root。
创建树（insert）
public void insert(int key)
{
Node p=new Node(); //待插入的节点
p.data=key; if(root==null)
{
root=p;
}
else
{
Node parent=new Node();
Node current=root;
while(true)
{
parent=current;
if(key>current.data)
{
current=current.right; // 右子树
if(current==null)
{
parent.right=p;
return;
}
}
else //本程序没有做key出现相等情况的处理，暂且假设用户插入的节点值都不同
{
current=current.left; // 左子树
if(current==null)
{
parent.left=p;
return;
}
}
}
}
}
创建树的时候，主要用到了parent，current来记录要插入节点的位置。哪么怎么检验自己是否正确地创建了一颗二叉搜索树呢，我们通过遍历来输出各个节点的值
遍历树（travel）
遍历指的是按照某种特定的次序来访问二叉搜索树中的每个节点，主要有三种遍历的方法：
- 前序遍历，“中左右”
- 中序遍历，“左中右”
- 后续遍历，“左右中”
上面的口诀“中左右”表示的含义是，先访问根节点，再访问左子，最后访问右子。举个例子：
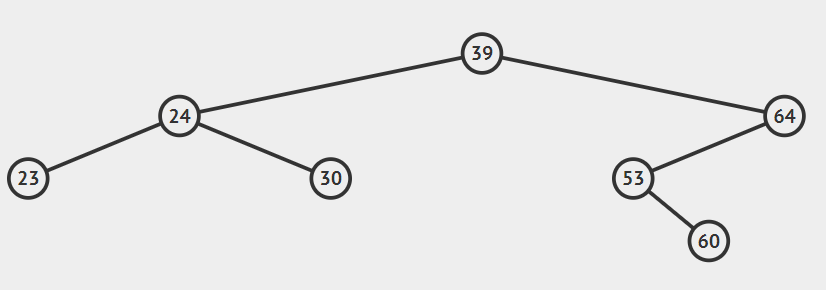
- 前序遍历：39 24 23 30 64 53 60
- 中序遍历：23 24 30 39 53 60 64
- 后序遍历：23 30 24 60 53 64 39
你会发现，按照中序遍历的规则将一个二叉搜索树输入，结果为按照正序排列。
public void preOrder(Node root)
{ // 前序遍历,"中左右"
if (root != null)
{
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
} public void inOrder(Node root)
{ // 中序遍历,"左中右"
if (root != null)
{
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
} public void postOrder(Node root)
{ // 后序遍历,"左右中"
if (root != null)
{
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
} public void traverse(int traverseType)
{ // 选择以何种方式遍历
switch (traverseType)
{
case 1:
System.out.print("preOrder traversal ");
preOrder(root);
System.out.println();
break;
case 2:
System.out.print("inOrder traversal ");
inOrder(root);
System.out.println();
break;
case 3:
System.out.print("postOrder traversal ");
postOrder(root);
System.out.println();
break;
}
}
以上的代码采用递归的方式实现三种遍历，为了方便我们使用，又写了一个traverse函数来实现选择哪种方式进行树的遍历。
这会儿就可以写单元测试了，我们首先创建一个二叉搜索树，然后分别使用“前序”，“中序”，“后序”来遍历输出树的所有节点。
public static void main(String[] args) //unit test
{
BinarySearchTree tree=new BinarySearchTree(); tree.insert(39);
tree.insert(24);
tree.insert(64);
tree.insert(23);
tree.insert(30);
tree.insert(53);
tree.insert(60); tree.traverse(1);
tree.traverse(2);
tree.traverse(3);
}
运行该单元测试，可以看到如下的结果：
查找节点（find）
public Node find(int key)
{ // 从树中按照关键值查找元素
Node current = root;
while (current.data != key)
{
if (key > current.data)
current = current.right;
else
current = current.left;
if (current == null) return null;
}
return current;
} public void show(Node node)
{ //输出节点的数据域
if(node!=null)
System.out.println(node.data);
else
System.out.println("null");
}
查找节点比较简单，如果找到节点则返回该节点，否则返回null。为了方便在控制台输出，我们有添加了一个show函数，用来输出节点的数据域。
删除节点（delete）
删除节点是二叉搜索树中，最复杂的一种操作，但是也不是特别难，我们分类讨论：
- 要删除节点有零个孩子，即叶子节点
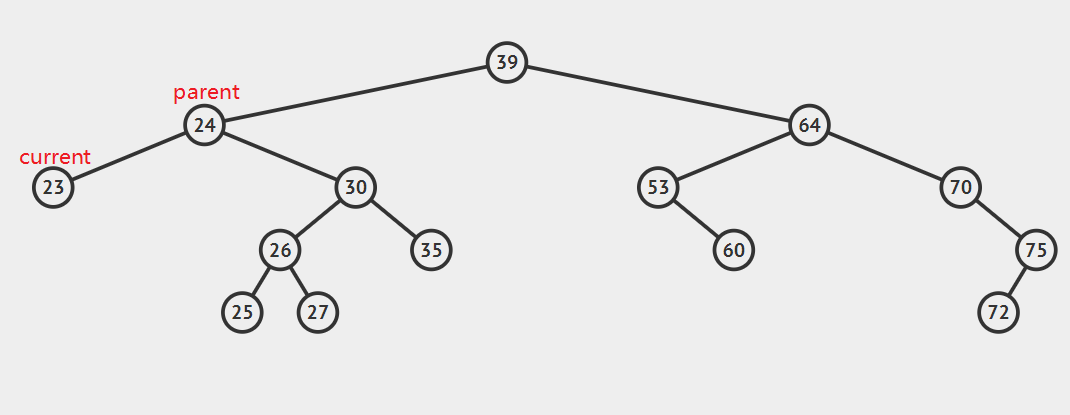
如图所示，只需要将parent.left(或者是parent.right)设置为null，然后Java垃圾自动回收机制会自动删除current节点。
- 要删除节点有一个孩子
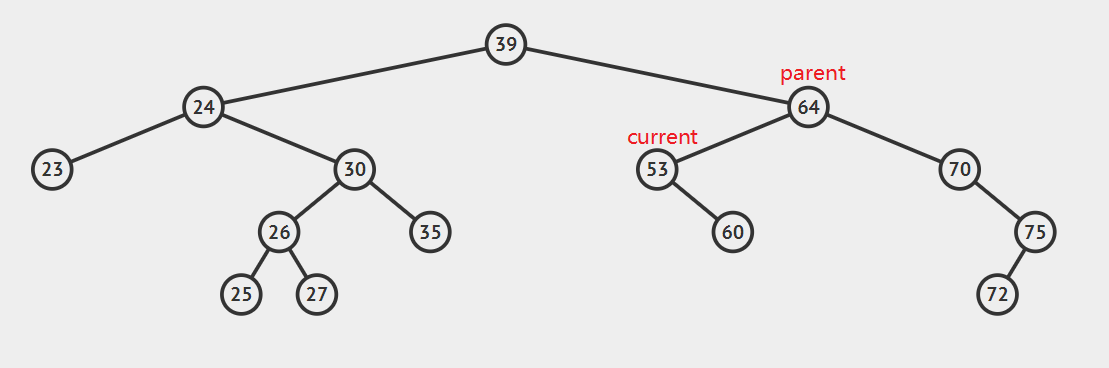
如图所示，只需要将parent.left(或者是parent.right)设置为curren.right(或者是current.left)即可。
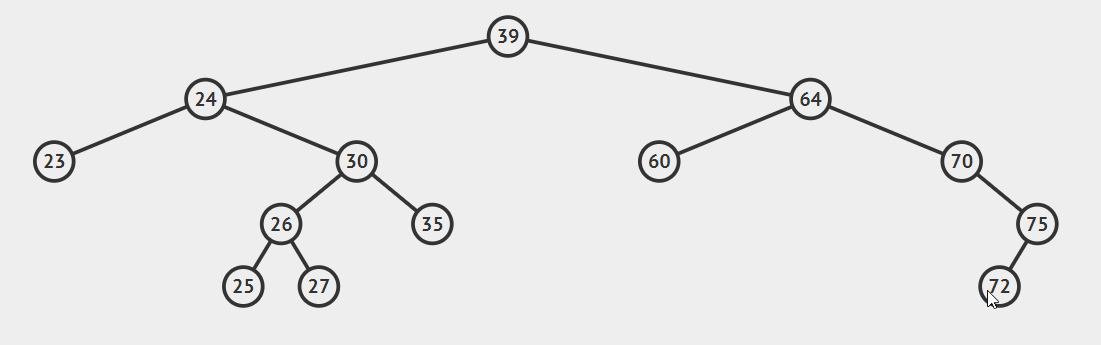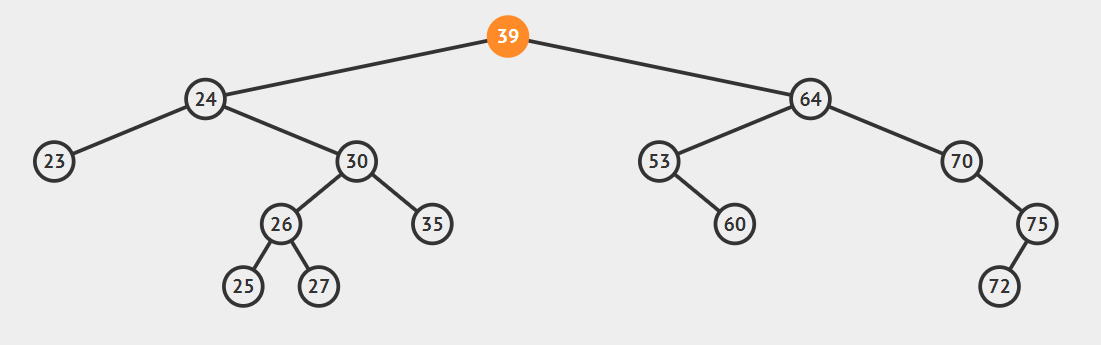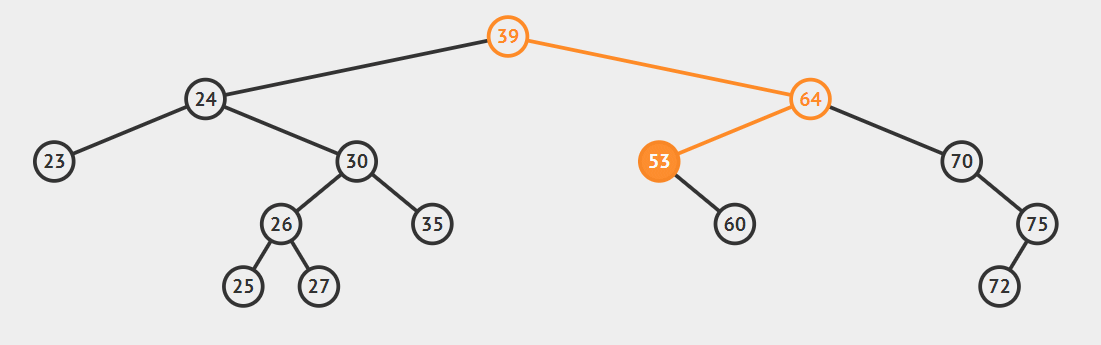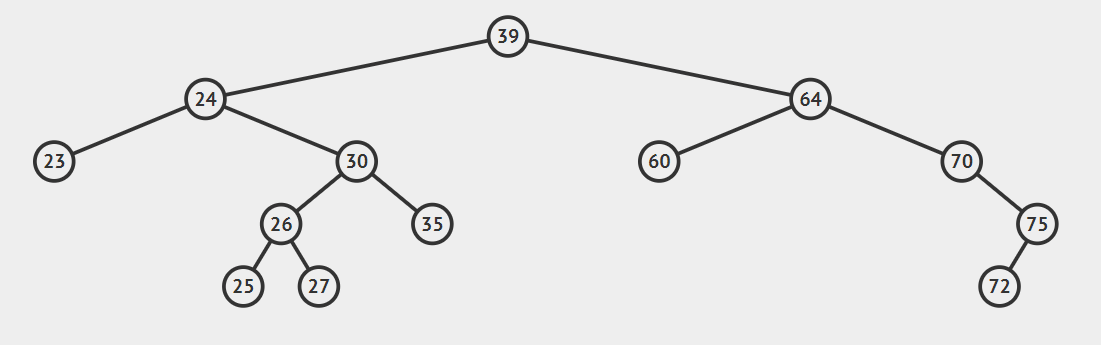
- 要删除节点有两个孩子
这种情况比较复杂，首先我们引入后继节点的概念，如果将一棵二叉树按照中序周游的方式输出，则任一节点的下一个节点就是该节点的后继节点。例如：上图中24的后继节点为25，64的后继节点为70.找到后继节点以后，问题就变得简单了，分为两种情况：
1.后继节点为待删除节点的右子，只需要将curren用successor替换即可，注意处理好current.left和successor.right.
注意：这种情况下，successor一定没有左孩子，一但它有左孩子，哪它必然不是current的后继节点。
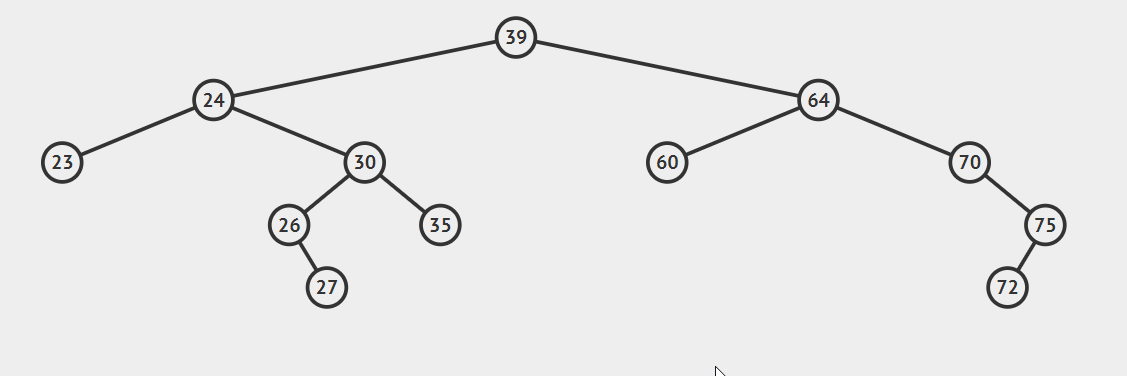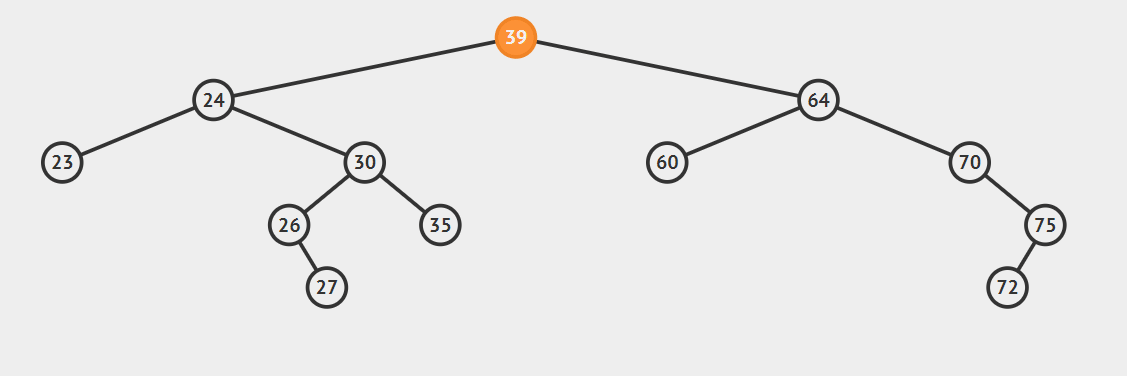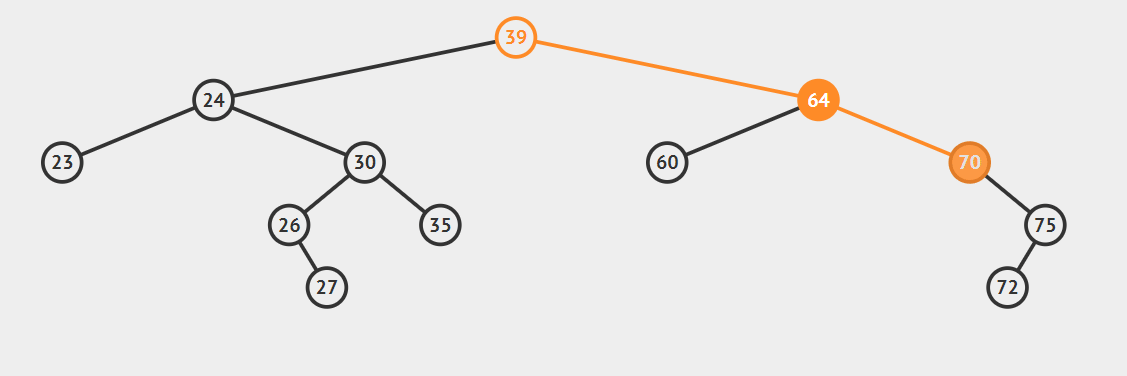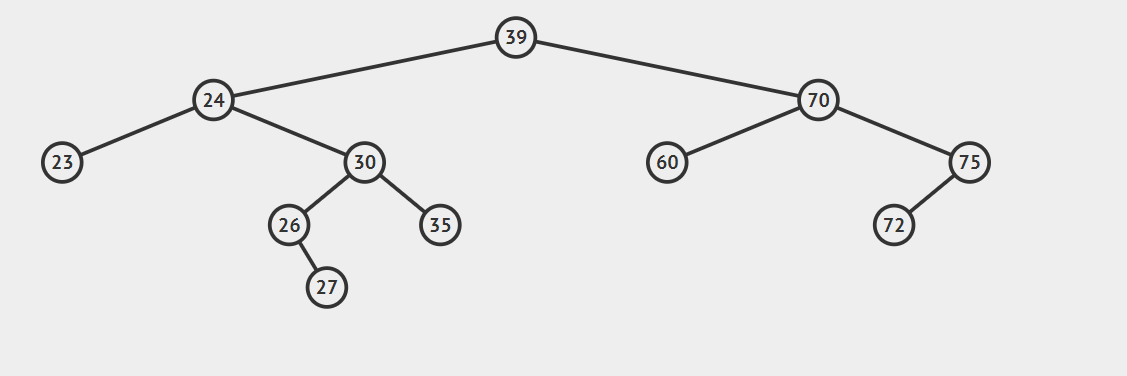
2.后继节点为待删除结点的右孩子的左子树，这种情况稍微复杂点，请看动态图片演示。
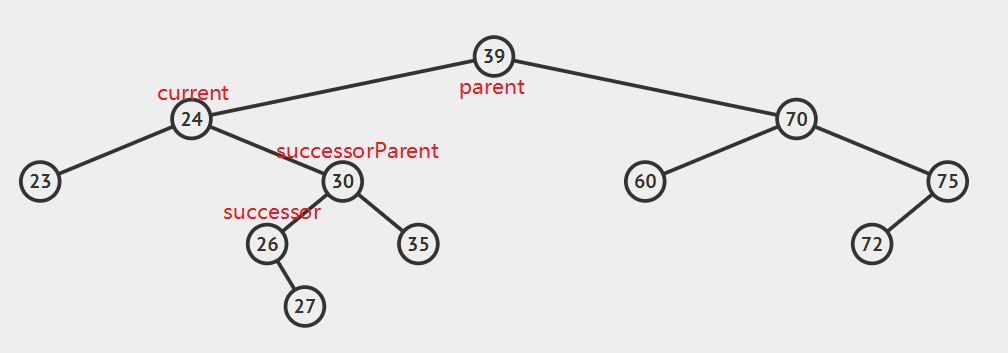
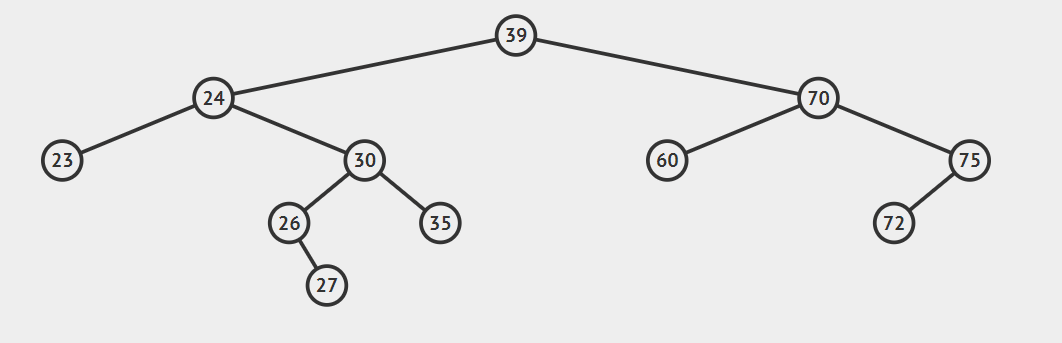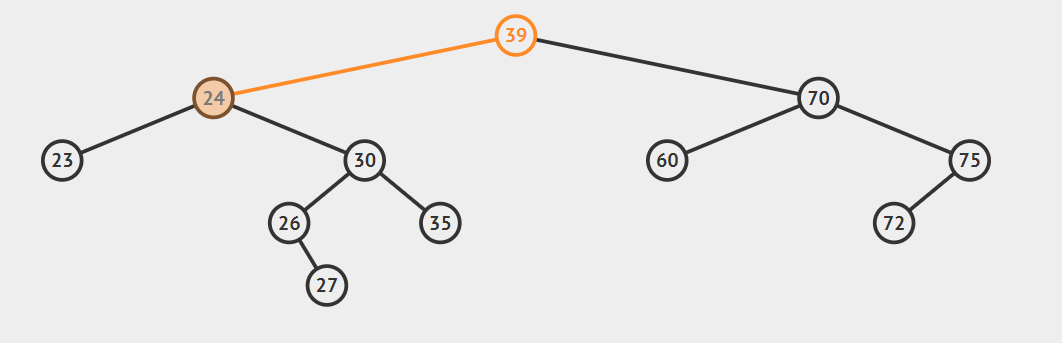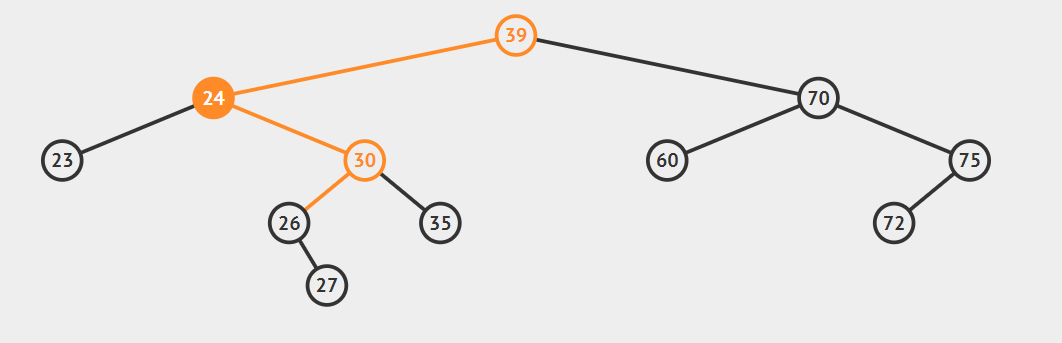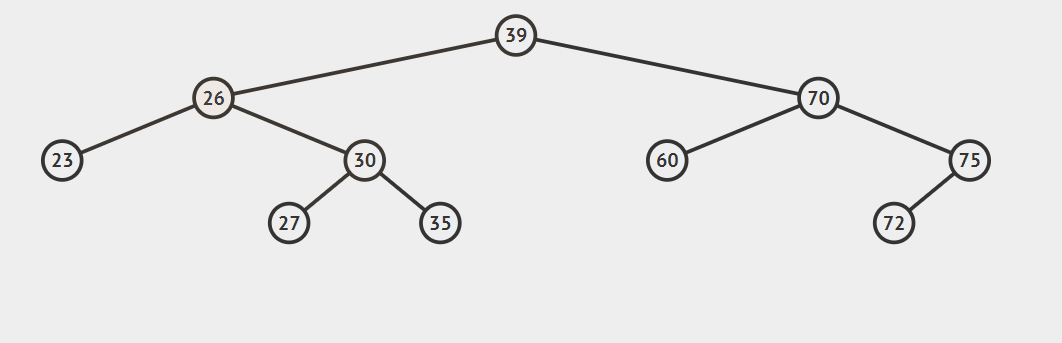
算法的步骤是：
- successorParent.left=successor.right
- successor.left=current.left
- parent.left=seccessor
弄懂原理后，我们来看具体的代码实现：
private Node getSuccessor(Node delNode) //寻找要删除节点的中序后继结点
{
Node successorParent=delNode;
Node successor=delNode;
Node current=delNode.right; //用来寻找后继结点
while(current!=null)
{
successorParent=successor;
successor=current;
current=current.left;
} //如果后继结点为要删除结点的右子树的左子，需要预先调整一下要删除结点的右子树
if(successor!=delNode.right)
{
successorParent.left=successor.right;
successor.right=delNode.right;
}
return successor;
} public boolean delete(int key) // 删除结点
{
Node current = root;
Node parent = new Node();
boolean isRightChild = true;
while (current.data != key)
{
parent = current;
if (key > current.data)
{
current = current.right;
isRightChild = true;
}
else
{
current = current.left;
isRightChild = false;
}
if (current == null) return false; // 没有找到要删除的结点
}
// 此时current就是要删除的结点,parent为其父结点
// 要删除结点为叶子结点
if (current.right == null && current.left == null)
{
if (current == root)
{
root = null; // 整棵树清空
}
else
{
if (isRightChild)
parent.right = null;
else
parent.left = null;
}
return true;
}
//要删除结点有一个子结点
else if(current.left==null)
{
if(current==root)
root=current.right;
else if(isRightChild)
parent.right=current.right;
else
parent.left=current.right;
return true;
}
else if(current.right==null)
{
if(current==root)
root=current.left;
else if(isRightChild)
parent.right=current.left;
else
parent.left=current.left;
return true;
}
//要删除结点有两个子结点
else
{
Node successor=getSuccessor(current); //找到要删除结点的后继结点 if(current==root)
root=successor;
else if(isRightChild)
parent.right=successor;
else
parent.left=successor; successor.left=current.left;
return true;
}
}
二叉搜索树删除操作
大家注意哪个私有函数getSuccessor的功能，它不仅仅是用来找后继结点的。
总结
二叉搜索树其实不是特别难，理解以后，多练习几次，应该可以掌握。以下是全部的代码：
package org.yahuian; public class BinarySearchTree
{ // 二叉搜索树类
private class Node
{ // 节点类
int data; // 数据域
Node right; // 右子树
Node left; // 左子树
} private Node root; // 树根节点 public void insert(int key)
{
Node p = new Node(); // 待插入的节点
p.data = key; if (root == null)
{
root = p;
}
else
{
Node parent = new Node();
Node current = root;
while (true)
{
parent = current;
if (key > current.data)
{
current = current.right; // 右子树
if (current == null)
{
parent.right = p;
return;
}
}
else // 本程序没有做key出现相等情况的处理，暂且假设用户插入的节点值都不同
{
current = current.left; // 左子树
if (current == null)
{
parent.left = p;
return;
}
}
}
}
} public void preOrder(Node root)
{ // 前序遍历,"中左右"
if (root != null)
{
System.out.print(root.data + " ");
preOrder(root.left);
preOrder(root.right);
}
} public void inOrder(Node root)
{ // 中序遍历,"左中右"
if (root != null)
{
inOrder(root.left);
System.out.print(root.data + " ");
inOrder(root.right);
}
} public void postOrder(Node root)
{ // 后序遍历,"左右中"
if (root != null)
{
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data + " ");
}
} public void traverse(int traverseType)
{ // 选择以何种方式遍历
switch (traverseType)
{
case 1:
System.out.print("preOrder traversal ");
preOrder(root);
System.out.println();
break;
case 2:
System.out.print("inOrder traversal ");
inOrder(root);
System.out.println();
break;
case 3:
System.out.print("postOrder traversal ");
postOrder(root);
System.out.println();
break;
}
} public Node find(int key)
{ // 从树中按照关键值查找元素
Node current = root;
while (current.data != key)
{
if (key > current.data)
current = current.right;
else
current = current.left;
if (current == null) return null;
}
return current;
} public void show(Node node)
{ //输出节点的数据域
if(node!=null)
System.out.println(node.data);
else
System.out.println("null");
} private Node getSuccessor(Node delNode) //寻找要删除节点的中序后继结点
{
Node successorParent=delNode;
Node successor=delNode;
Node current=delNode.right; //用来寻找后继结点
while(current!=null)
{
successorParent=successor;
successor=current;
current=current.left;
} //如果后继结点为要删除结点的右子树的左子，需要预先调整一下要删除结点的右子树
if(successor!=delNode.right)
{
successorParent.left=successor.right;
successor.right=delNode.right;
}
return successor;
} public boolean delete(int key) // 删除结点
{
Node current = root;
Node parent = new Node();
boolean isRightChild = true;
while (current.data != key)
{
parent = current;
if (key > current.data)
{
current = current.right;
isRightChild = true;
}
else
{
current = current.left;
isRightChild = false;
}
if (current == null) return false; // 没有找到要删除的结点
}
// 此时current就是要删除的结点,parent为其父结点
// 要删除结点为叶子结点
if (current.right == null && current.left == null)
{
if (current == root)
{
root = null; // 整棵树清空
}
else
{
if (isRightChild)
parent.right = null;
else
parent.left = null;
}
return true;
}
//要删除结点有一个子结点
else if(current.left==null)
{
if(current==root)
root=current.right;
else if(isRightChild)
parent.right=current.right;
else
parent.left=current.right;
return true;
}
else if(current.right==null)
{
if(current==root)
root=current.left;
else if(isRightChild)
parent.right=current.left;
else
parent.left=current.left;
return true;
}
//要删除结点有两个子结点
else
{
Node successor=getSuccessor(current); //找到要删除结点的后继结点 if(current==root)
root=successor;
else if(isRightChild)
parent.right=successor;
else
parent.left=successor; successor.left=current.left;
return true;
}
} public static void main(String[] args) // unit test
{
BinarySearchTree tree = new BinarySearchTree(); tree.insert(39);
tree.insert(24);
tree.insert(64);
tree.insert(23);
tree.insert(30);
tree.insert(53);
tree.insert(60); tree.traverse(1);
tree.traverse(2);
tree.traverse(3); tree.show(tree.find(23));
tree.show(tree.find(60));
tree.show(tree.find(64)); tree.delete(23);
tree.delete(60);
tree.delete(64); tree.show(tree.find(23));
tree.show(tree.find(60));
tree.show(tree.find(64));
}
}
二叉搜索树详解
动态图片来自于：https://visualgo.net/en/bst
二叉搜索树详解（Java实现）的更多相关文章
- 数据结构图文解析之：二叉堆详解及C++模板实现
0. 数据结构图文解析系列 数据结构系列文章 数据结构图文解析之:数组.单链表.双链表介绍及C++模板实现 数据结构图文解析之:栈的简介及C++模板实现 数据结构图文解析之:队列详解与C++模板实现 ...
- 7-4 是否同一棵二叉搜索树 (25分) JAVA
给定一个插入序列就可以唯一确定一棵二叉搜索树.然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到. 例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结 ...
- 剑指Offer:面试题27——二叉搜索树与双向链表(java实现)
问题描述: 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表.要求不能创建任何新的结点,只能调整树中结点指针的指向. 思路: 将树分为三部分:左子树,根结点,右子树. 1.我们要把根结点与左 ...
- 95题--不同的二叉搜索树II（java、中等难度）
题目描述:给定一个整数 n,生成所有由 1 ... n 为节点所组成的 二叉搜索树 . 示例如下: 分析:这一题需要对比LeetCode96题来分析:https://www.cnblogs.com/K ...
- AVL树(二叉平衡树)详解与实现
AVL树概念 前面学习二叉查找树和二叉树的各种遍历,但是其查找效率不稳定(斜树),而二叉平衡树的用途更多.查找相比稳定很多.(欢迎关注数据结构专栏) AVL树是带有平衡条件的二叉查找树.这个平衡条件必 ...
- 《剑指offer》面试题27 二叉搜索树与双向链表 Java版
(将BST改成排序的双向链表.) 我的方法一:根据BST的性质,如果我们中序遍历BST,将会得到一个从小到大排序的序列.如果我们将包含这些数字的节点连接起来,就形成了一个链表,形成双向链表也很简单.关 ...
- 二叉搜索树（BST）详解
前言:平衡树的前置知识吧 二叉搜索树的定义: 二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树: (1)若左子树不空,则左子树上所有结点的值均小于或等于它的根节点的值: (2)若右子树不空,则右子 ...
- 【算法与数据结构】二叉搜索树的Java实现
为了更加深入了解二叉搜索树,博主自己用Java写了个二叉搜索树,有兴趣的同学可以一起探讨探讨. 首先,二叉搜索树是啥?它有什么用呢? 二叉搜索树, 也称二叉排序树,它的每个节点的数据结构为1个父节点指 ...
- Java实现二叉搜索树的添加，前序、后序、中序及层序遍历，求树的节点数，求树的最大值、最小值，查找等操作
什么也不说了,直接上代码. 首先是节点类,大家都懂得 /** * 二叉树的节点类 * * @author HeYufan * * @param <T> */ class Node<T ...
随机推荐
- 13.Python略有小成(装饰器,递归函数)
Python(装饰器,递归函数) 一.开放封闭原则 软件面世时,不可能把所有的功能都设计好,再未来的一两年功能会陆续上线,定期更新迭代,软件之前所用的源代码,函数里面的代码以及函数的调用方式一般不 ...
- $.extend(),与$.fn.extend() 讲解（一）
jQuery插件的开发包括两种: 一种是类级别的插件开发,即给jQuery添加新的全局函数,相当于给jQuery类本身添加方法.jQuery的全局函数就是属于jQuery命名空间的函数,另一种是对象级 ...
- vue中的导航守卫
官方文档地址: 导航守卫:https://router.vuejs.org/zh-cn/advanced/navigation-guards.html 好的,重点内容 router.beforeEac ...
- Net Core 2.0生态1
Net Core 2.0生态 阅读目录 前言:答读者问(time by:2017.8.19) 项目升级到ASP.NET Core 2.0 新增功能:Razor Pages介绍 模板更新 Entity ...
- RabbitMQ使用教程（一）RabbitMQ环境安装配置及Hello World示例
你是否听说过或者使用过队列? 你是否听说过或者使用过消息队列? 你是否听说过或者使用过RabbitMQ? 提到这几个词,用过的人,也许觉得很简单,没用过的人,也许觉得很复杂,至少在我没使用消息队列之前 ...
- CQRS之旅——旅程4(扩展和增强订单和注册限界上下文)
旅程4:扩展和增强订单和注册限界上下文 进一步探索订单和注册的有界上下文. "我明白,如果一个人想看些新鲜的东西,旅行并不是没有意义的."儒勒·凡尔纳,环游世界80天 对限界上下文 ...
- Centos7.2内网环境安装MySQL5.7.24
1.配置本地yum源 内网环境,首先需要配置本地yum源,以解决MySQL的依赖安装,具体参考该文:点击打开 2.查看服务器环境 uname -a 3.去官网下载MySQL安装包 MySQL官网网址: ...
- Spring连接数据库
public class Book { private int bookid; private String bookname; private String bookauthor; private ...
- 自动生成sql
添加下面这个类 public static class GetAllAttribute<T> where T : class { public static string Names; p ...
- pageContext.setAttribute的使用场合
由于页面间跳转以后,pageScope域失效,所以,关于pageContext.setAttribute和pageContext.getAttribute的使用(pagecontext作用域是page ...