AI数学基础之:确定图灵机和非确定图灵机

目录

• 简介
• 图灵机
• 图灵机的缺点
• 等效图灵机
  • 确定图灵机
  • 非确定图灵机

简介

图灵机是由艾伦·麦席森·图灵在1936年描述的一种抽象机器，它是人们使用纸笔进行数学运算的过程的抽象，它肯定了计算机实现的可能性，并给出了计算机应有的主要架构，引入了读写与算法与程序语言的概念为现代计算机的发明打下了基础。

本文将会讲解一下图灵机中的两种类型：确定图灵机和非确定图灵机。

图灵机

图灵机是一种数学计算模型，它定义了一个抽象机器，该抽象机器根据规则表来操纵带子上的符号。尽管该模型很简单，但是在任何给定计算机算法的情况下，都可以构建出模拟该算法逻辑的图灵机。

简单点说，图灵机就是一个模拟算法运行的抽象机器。它是这样定义的：

1. 有一个无限长度的磁带，这个磁带被分成了一个接一个的单元格，磁带被用于写入字母和符号。
2. 一个读写磁带的磁头，这个磁头负责控制堆磁带的写入和左右移动。
3. 一个状态寄存器，用来存储图灵机的状态。
4. 一个指令表，可以根据机器当前所处的状态和磁带上当前的符号，指示机器进行特定的操作。比如：擦除或者写入一个符号、向左或者向右移动磁头。

可以看到整个图灵机基本上模拟了程序的执行步骤。

图灵机虽然可以表示任意的计算程序，但是因为其极其简单的设计实际上并不适合进行计算，所以现实世界的现代计算机都是对图灵机的优化设计。

图灵完备性是指指令系统模拟图灵机的能力。从理论上讲，图灵完整的一种编程语言可以表达计算机可以完成的所有任务。如果忽略有限内存的限制，几乎所有编程语言都是图灵完备的。

图灵机的缺点

虽然图灵机可以表示任何计算任务，但是图灵机太过于简单了，在某些复杂的模型中无法很好的进行使用。比如在现代计算机中的RASP随机存储模型，因为RASP可以在寄存器中引用其他的寄存器，所以可以基于内存索引进行优化，这种优化是在图灵机中无法实现的。

图灵机的另一个限制是它们不能很好地进行并发建模。另外，因为在早期的时候，计算机的使用通常仅限于批处理，即非交互式任务，每个任务都从给定的输入数据中产生输出数据。 所以图灵机在描述现代交互式应用也有一些限制。

等效图灵机

因为图灵机是一种假想的设备，它为计算机算法的概念提供了理论基础。并且因为图灵机模型比较简单，对于复杂问题的描述比较弱，所以出现了很多图灵机的等效模型，虽然这些模型并不一定比图灵机强大，但是这些模型是真正存在的，并且使用他们可以更加容易的解决特定问题。

确定图灵机

在确定性图灵机（DTM）中，其控制规则规定了在任何给定情况下最多只能执行一个动作。

确定性图灵机具有转换功能，对于磁带头下的给定状态和符号，该转换功能指定了三件事：

要写入磁带的符号，头部应移动的方向（向左，向右或都不向），以及有限控制的后续状态。

例如，状态3的磁带上的X可能会使DTM在磁带上写Y，将磁头向右移动一个位置，然后切换到状态5。

非确定图灵机

在理论计算机科学中，非确定性图灵机（NTM）是一种理论计算模型，其控制规则在某些给定情况下指定了多个可能的动作。 也就是说，NTM的下一个状态不是完全由其动作和它所看到的当前符号决定的（不同于确定性图灵机）。

例如，状态3的磁带上的X可能允许NTM：

输入Y，向右移动，然后切换到状态5或者写一个X，向左移动，并停留在状态3。

那么问题来了，对于非确定图灵机来说是怎么进行下一步的选择的呢？实际上NTM足够幸运，它总是会选择那个能够最终指向接受状态的那一步。

你可以把NTM的诸多分支看成是许多副本，每个副本遵循一个可能的转换。 DTM遵循的是单个“计算路径”，而NTM则是“计算树”。 如果树中至少有一个分支导致接受状态，那么NTM就会接受这个输入状态。

我们看下两者的决策图：

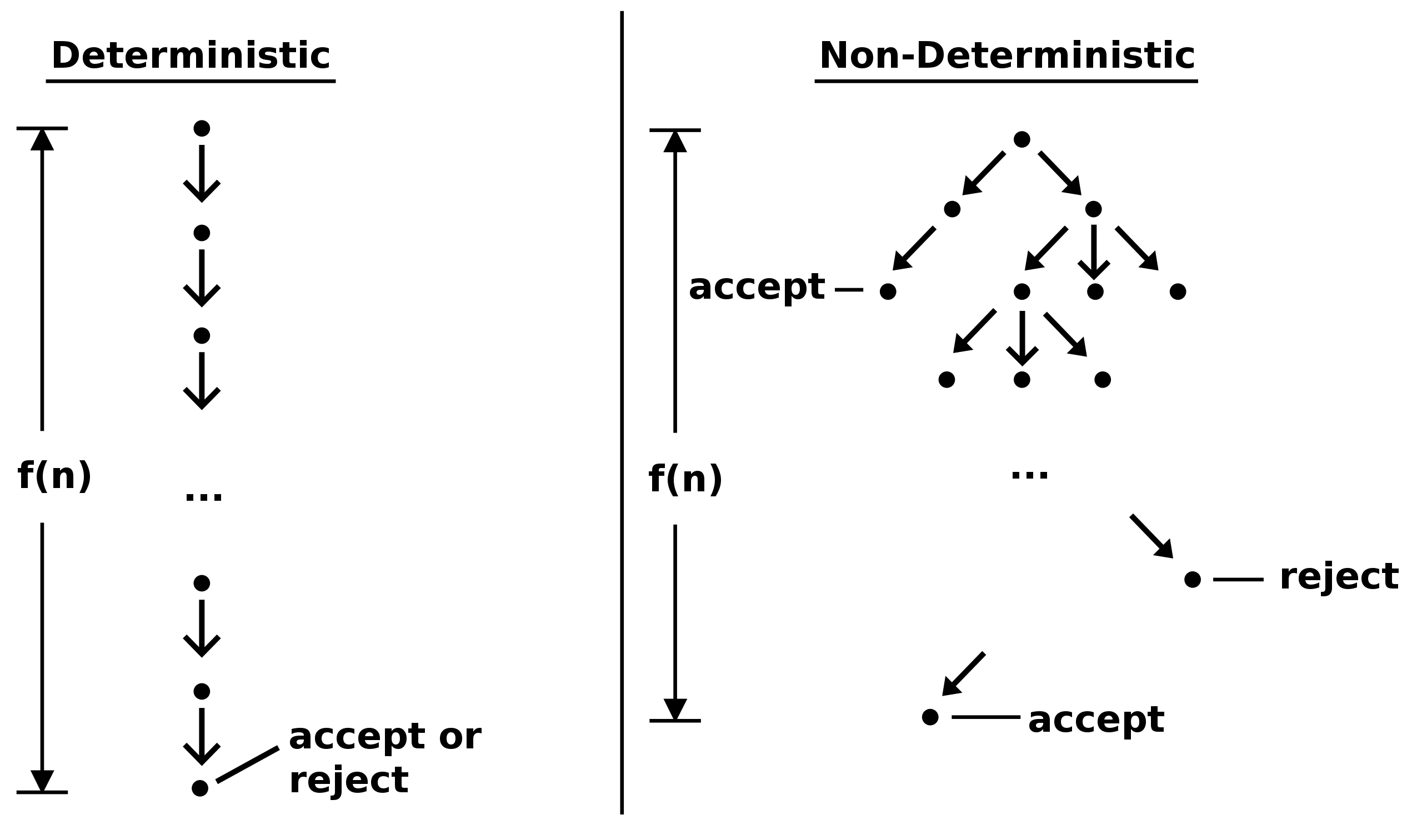
确定图灵机和非确定图灵机 两者在计算上是等效的，也就是说，尽管它们通常具有不同的运行时，但可以将任何NDTM转换为DTM（反之亦然）。 这可以通过构造来证明。

本文已收录于 http://www.flydean.com/03-turing-machine/

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！