[Fundamental of Power Electronics]-PART I-2.稳态变换器原理分析-2.4 Cuk变换器实例

2.4 Cuk 变换器

作为第二个示例，考虑图2.20（a）的变换器。该变换器执行类似于降压-升压变换器的直流转换功能：它可以增加或减小直流电压的幅值，并且可以反转极性。使用晶体管和二极管的实际实现如图2.20（b）所示。

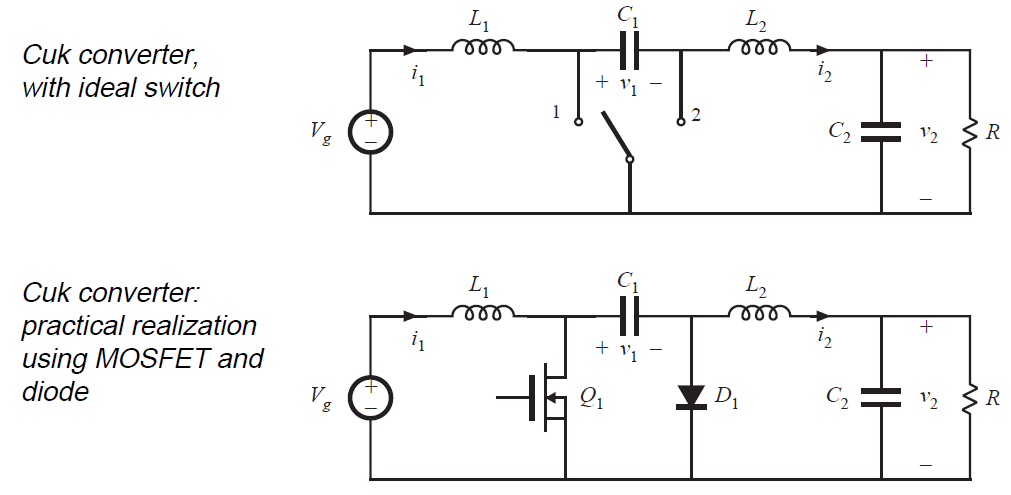
Fig 2.20 Cuk converter example

这个变换器通过电容能量传输进行工作。如图2.21所示，当开关位于位置2时，电容 \(C_{1}\) 通过电感\(L_{1}\)连接到输入电源，电源能量存储在\(C_{1}\)中。当开关处于位置1时，该能量通过\(L_{2}\)释放到负载。

在图2.20（a）中定义了电感电流和电容电压，并在一定程度上任意分配了极性(正负号）。在本节中，将应用电感伏秒平衡和电容电荷平衡的原理来得出电感电流和电容电压的直流分量。并且计算电压和电流纹波幅度。

在第一个子间隔期间，当开关处于位置1时，转换器电路变为图2.21（a）。电感电压和电容电流为：

\[v_{L1}=V_{g}\\
v_{L2}=-v_{1}-v_{2}\\
i_{C1}=i_{2}\\
i_{C2}=i_{2}-\frac{v_{2}}{R} \tag{2.48}
\]

接下来，我们假设和直流分量\(I_{1},I_{2},V_{1},V_{2}\)相比，其开关纹波幅值\(i_{1}(t),i_{2}(t),v_{1}(t),v_{2}(t)\)非常小，这时候可以用小纹波近似，即：

\[v_{L1}=V_{g}\\
v_{L2}=-V_{1}-V_{2}\\
i_{C1}=I_{2}\\
i_{C2}=I_{2}- \frac{V_{2}}{R} \tag{2.49}
\]

在第二个子间隔中，将开关置于位置2时，变换器电路元件的连接如图2.21（b）所示。电感电压和电容电流为：

\[v_{L1}=V_{g}-v_{1} \\
v_{L2}=-v_{2} \\
i_{C1}=i_{1} \\
i_{C2}=i_{2}- \frac{v_{2}}{R} \tag{2.50}
\]

同样进行小纹波近似

\[v_{L1}=V_{g}-V_{1}\\
v_{L2}=-V_{2}\\
i_{C1}=I_{1}\\
i_{C2}=I_{2}- \frac{V_{2}}{R} \tag{2.51}
\]

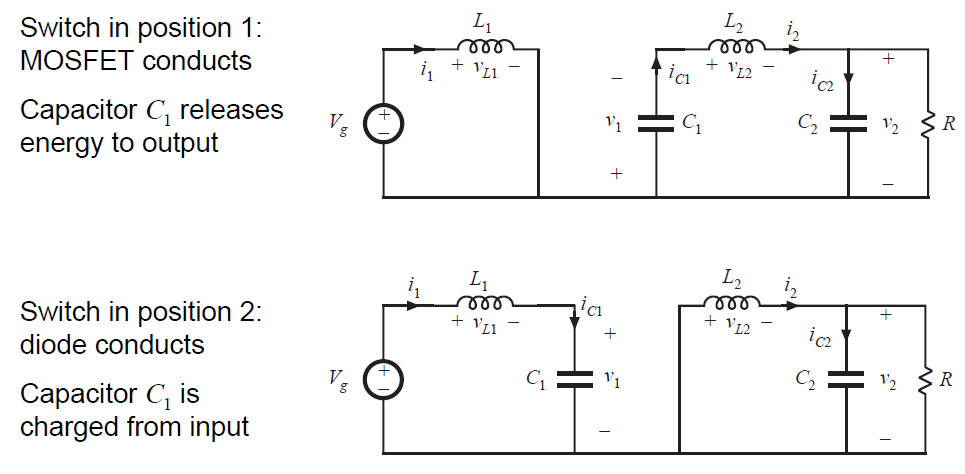
Fig 2.21 Cuk converter circuit with switch in positions 1 and 2

公式（2.49）和（2.51）用于绘制图2.22中的电感电压和电容电流波形。

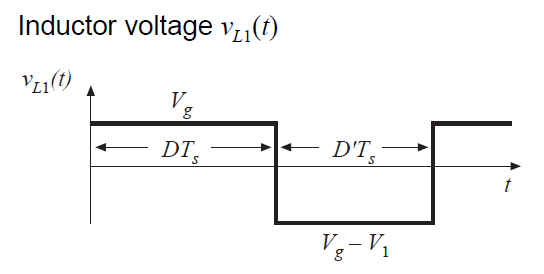
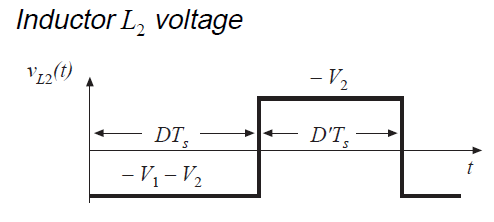
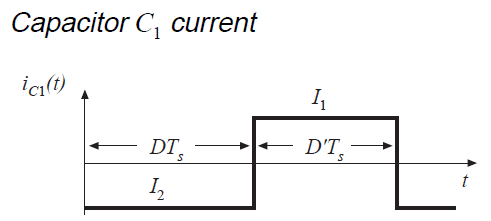
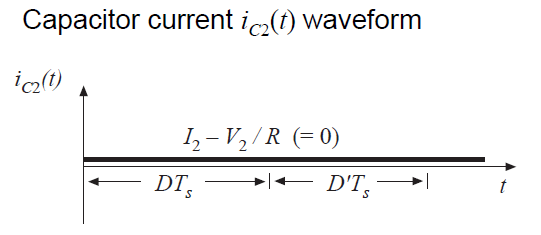
Fig 2.22 Cuk converter waveforms

下一步是将图2.22的波形的直流分量或平均值等效为零，以找到变换器中的稳态条件。结果是：

\[<v_{L1}>=D V_{g}+D^{'}(V_{g}-V{1})\\
<v_{L2}>=D(-V_{1}-V_{2})+D^{'}(-V_{2})=0\\
<i_{C1}>=DI_{2}+D^{'}I_{1}=0\\
<i_{C2}>=I_{2}- \frac{V_{2}}{R} \tag{2.52}
\]

求解电容电压与电感电流平均值为

\[V_{1}= \frac{V_{g}}{D^{'}} \\
V_{2}= -\frac{D}{D^{'}}V_{g} \\
I_{1}=- \frac {D}{D^{'}} I_{2}=(\frac{D}{D^{'}})^2 \frac{V_{g}}{R}\\
I_{2}= \frac{V_{2}}{R}=- \frac{D}{D^{'}} \frac{V_{g}}{R} \tag{2.53}
\]

直流输出电压\(V_{2}\)与占空比D之间关系在图2.23中给出

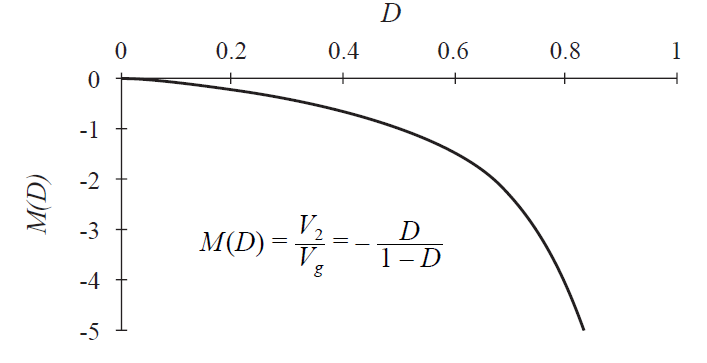
Fig 2.23 Cuk converter conversion ratio M = V/Vg

电感电流以及电容电压波形如图2.24(a)-(c)所示，第一个子间隔区间各波形斜率如下所示

\[\frac{di_{1}(t)}{dt}= \frac{v_{L1}(t)}{L_{1}} = \frac{V_{g}}{L_{1}}\\
\frac{di_{2}(t)}{dt}= \frac{v_{L2}(t)}{L_{1}} = \frac{-V_{1}-V_{2}}{L_{2}}\\
\frac{dv_{1}(t)}{dt}= \frac{i_{C1}(t)}{C_{1}} = \frac{I_{2}}{C_{1}} \tag{2.54}
\]

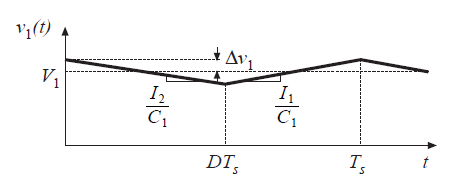
Fig 2.24 Inductor current waveforms and Capacitor C1 waveform

第二个时间间隔内，各波形斜率如下所示：

\[\frac{di_{1}(t)}{dt}= \frac{v_{L1}(t)}{L_{1}} = \frac{V_{g}-V_{1}}{L_{1}}\\
\frac{di_{2}(t)}{dt}= \frac{v_{L2}(t)}{L_{1}} = \frac{-V_{2}}{L_{2}}\\
\frac{dv_{1}(t)}{dt}= \frac{i_{C1}(t)}{C_{1}} = \frac{I_{2}}{C_{1}} \tag{2.55}
\]

在第二个子区间内，使用式(2.51)中相应参数代替\(v_{L1},v_{L2},i_{C1}\)

在第一个子区间内，使用\(2\Delta i_{1},-2 \Delta i_{2}\)，和\(-2 \Delta v_{1}\)，来代替\(i_{1}(t),i_{2}(t)\)，和\(v_{1}(t)\)的改变量。这些变化量除以区间长度\(D T_{s}\)，就等于公式(2.54)中的各个斜率。我们得到

\[\Delta i_{1}= \frac{V_{g} D T_{s}}{2 L_{1}} \\
\Delta i_{2}= \frac{V_{1}+V_{2}}{2 L_{2}} D T_{s} \\
\Delta v_{1}= \frac{- I_{2} D T_{s}}{2 C_{1}} \tag{2.56}
\]

公式(2.53)中的直流量关系，可以用来简化上式，代替\(V_{1},V_{2}\)，和\(I_{1}\)，我们得到

\[\Delta i_{1}= \frac{V_{g} D T_{s}}{2 L_{1}} \\
\Delta i_{2}= \frac{V_{g} D T_{s}}{2 L_{2}} \\
\Delta v_{1}= \frac{V_{g} D^2 T_{s}}{2 D^{'} R C_{1}} \tag{2.57}
\]

同样的，这个公式可以在各个纹波量确定后，用来确定\(L_{1},L_{2},C_{1}\)的值。

类似的方法却不能用来计算输出滤波电容电压\(V_{2}(t)\)的纹波幅值。根据图2.22(d)，电流\(i_{C2}(t)\)是连续的,不像\(v_{L1},v_{L2},i_{C1}\)，它是非脉动的。如果\(i_{2}(t)\)的开关纹波被忽略了，那么\(i_{C2}(t)\)就不含交流分量，然后根据小纹波近似得到结论，输出开关纹波\(\Delta v_{2}\)为0。

当然，输出电压纹波并不是0，要估算变换器输出电压纹波大小，就不能忽略电感电流\(i_{L2}(t)\)中的开关纹波，因为这个纹波是输出电容电压波动的唯一交流来源。下一节将讨论如何使用简化的方法分析Cuk变换器以及其他变换器中类似的问题。