Poj-P2533题解【动态规划】

本文为原创，转载请注明：http://www.cnblogs.com/kylewilson/

题目出处：

题目描述：

如果a_i1 < a_i2 < ... < a_ik ，1 <= i₁ < i₂ < ... < i_K <= N，则该序列为有序；给一个序列，找出一个最长的上升序列，如 (a₁, a₂, ..., a_N)有一个上升序列为 (a_i₁, a_i₂, ..., a_{i_K}),1 <= i₁ < i₂ < ... < i_K <= N；

例如 (1, 7, 3, 5, 9, 4, 8) 有上升序列如 (1, 7), (3, 4, 8)，最长的上升序列为(1, 3, 5, 8)，长度为4

求一个最长上升序列的长度

输入：

第一行一个数N，表示给定序列长度为N，1 <= N <= 1000

第二行N个数，表示序列的每个数值，每个数范围为[0,10000]

1 7 3 5 9 4 8

思路分析：

题目是一个求最优解的问题，所以首先想到的就是用动态规划的思想来解决。

动态规划的本质就是先求解小问题的最优解，再通过小问题的最优解推导出大问题的最优解。

下面就通过这个题目，来说明如何找出一个问题背后蕴含的动态规划本质。

我常用的方法，暂且称之为“最终状态反推法”。。。

步骤一：

假设一个最终的状态。

比如该题目，最终的状态一定是在该数组中选出部分的数字，并且选出的数字组成一个上升的序列，因为对于每一个数要么选择，要么不选。

如图P1.1, 红色框里的数字就是一个合理的最终状态。[1, 3, 5, 7]为上升序列，且长度为4是一个最优解。

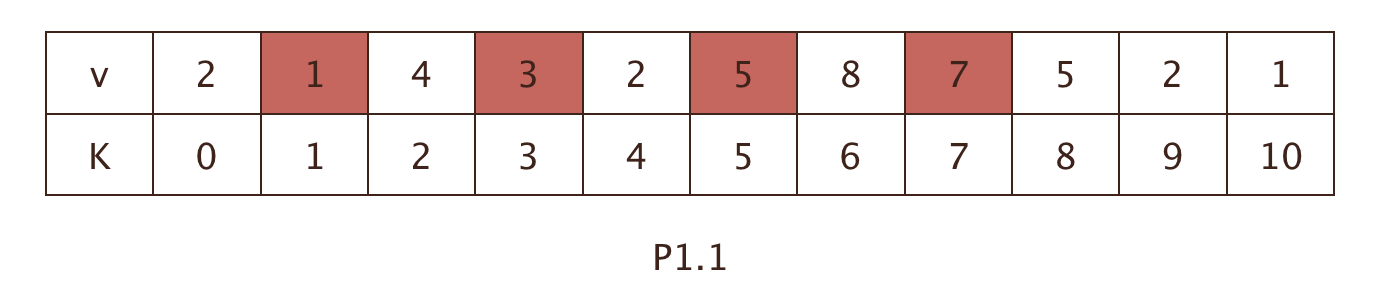
步骤二：

通过已知的最终状态扩大数据规模。

步骤一就是找小问题的解，我们其实也并没有真正去讲怎么找一个最优解，只是先假设一个最优解就是如上所示。

然后用上面的状态，去扩大数据规模，有点类似数学归纳法的思想。

如图P1.2

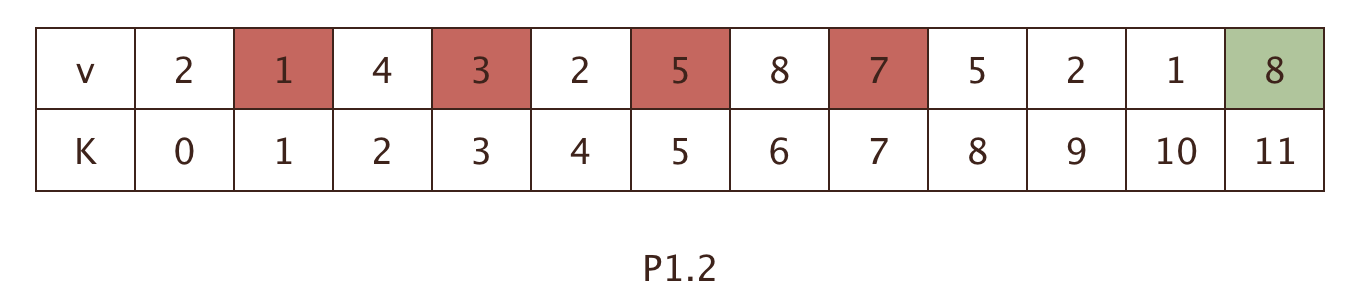
如果在原数组的最后一位再增加一个数，比如绿色框里的数字8，这种操作可以抽象为把N个数的数组扩大为N+1。

然后再结合步骤一中是如何假设的最终状态呢？

对于每一个数字要么选，要么不选，就只有两种情况。

情况1

如果增加的数字不选，N+1个数的最优解还是和N个数的最优解是一样的

设F[n]表示N个数能组成上升序列的最长长度，则F[n+1]=F[n]

情况2

如果增加的数字要选，则N+1个数的最优解可以通过N个数推导出来，即F[n+1]=F[n]+1，因为多选了一个数，所以肯定是加1。

步骤三

找出策略及条件。

现在也就是要详细分析一下上面的不同情况，具体是应该如何去选择。

比如一个很具体的问题，既然上面我们说到了，要么选择，要么不选择，那么你就会问，什么时候应该选择，什么时候不选择呢？

再回到题目结合具体的问题背景，我们是要找一个上升序列。对于步骤二中的情况1，如果该数要选择，自然就是增加的数是大于F[n]的解中最后的那一个数，如图P1.2。

对于步骤二中的情况2，如果该数不选择，也自然就是增加的数小于F[n]的解中最后的那一个数，如图P1.3

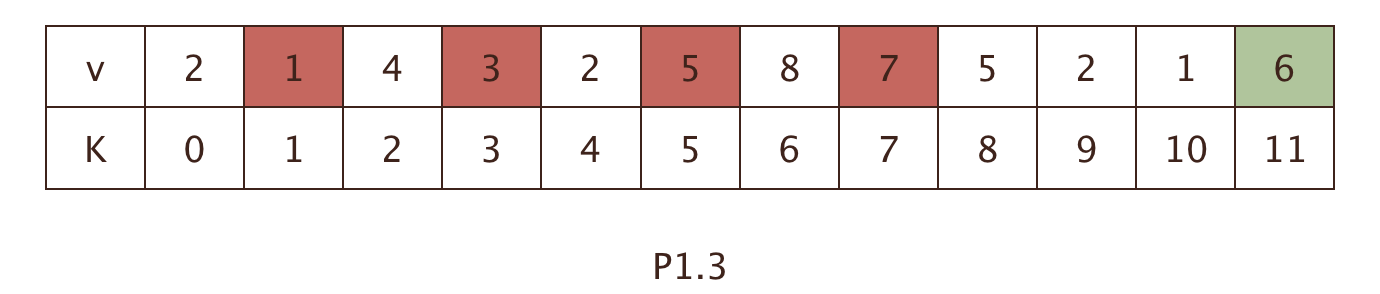
上面又引入了一个新的问题，必须知道之前的最优解具体选择了哪些数，不过其实我只关心最后的那一个数，那就是最后的那一个数必须要记录下来。

步骤四

找出状态及递推公式。

对于之前的F[n]只记录了长度，这明显是不够的，所以没法递推。

我们重新假设状态，

以f[i][j]表示前i个数中以第j个数结尾的最优长度，则递推公式如下：

f[i][i]=f[i-1][j]+1，其中a[i]>a[j]，即第i个数选择

f[i][j]=f[i-1][j]，其中 0<j<i，即第i个数不选择

最后遍历f[n][i]， 0<i<n，便可得到最优解

但到此还没有结束，因为动态规划中的状态与决策可以有很多的定义，本质也是一个优化剪枝的穷举，所以不同的状态与决策有不同的效率。

再仔细思想，我只需要知道上一次最优解最后选择的那一个数是多少；

则假设f[i]表示以第i个数结尾的最大长度

f[i]=max(f[j]+1)，其中a[i]>a[j]，

f[i]=1，其中a[i]不大于前面任何一个解的最后一个数，

最后遍历f[i]，0<i<=n，便可得到最优解。

C++源码如下：

github: https://github.com/Kyle-Wilson1/Poj/tree/master/P2533

#include <iostream>
#include <fstream>
#include <vector>
 
using namespace std;
 
int maxOfTwo(int a, int b) {
    return a > b ? a : b;
}
 
int main() {
 
    ifstream fin("a.in");
    ofstream fout("a.out");
 
    int i, j, n, maxLength = 0;
    fin >> n;
 
    vector<int> num(n, 0);
    vector<int> f(n, 0);
 
    for (i = 0; i < n; i++) {
        fin >> num[i];
    }
 
    for (i = 0; i < n; i++) {
        f[i] = 1;
        for (j = 0; j < i; j++) {
            if (num[i] > num[j]) {
                f[i] = maxOfTwo(f[i], f[j] + 1);
            };
        }
        maxLength = maxOfTwo(maxLength, f[i]);
    }
 
    fout << maxLength << endl;
    fin.close();
    fout.close();
 
    return 0;
}