【算法•日更•第三十五期】FF算法优化：EK算法

▎写在前面

　　FF算法传送门

　　之前我们已经学过了FF算法（全称Ford-Fulkerson算法）来找最大流，但是这种算法仍有诸多不对的地方。

　　其实这种算法存在着严重的效率的问题，请看下面的图：

　　

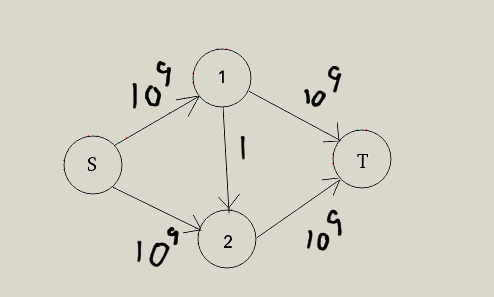
　　以这个图为例，我们使用的搜索是无规则选边的，可能第一次会选这样的一条边。

　　

　　那么我们继续增广。

　　

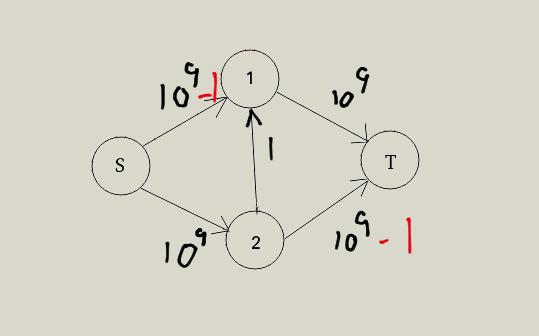
　　第二次我们可能会选这样一条边：

　　

　　

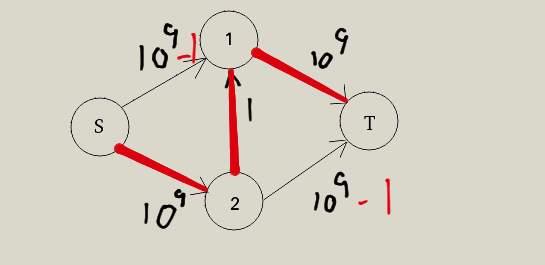
　　发现什么了没有？边一直在减1,那么如果这样循环下去，的确有严重的效率问题。

　　但是我们明明可以通过S -> 1 -> T或S -> 2 -> T就可以到达，且不存在效率问题，但是人眼能分辨出来，程序可不行，那么我们就应该请出EK算法了。

▎Edmonds-Karp算法

☞『定义』

　　该算法与Ford-Fulkerson算法相同，只是定义了找到增广路径时的搜索顺序。 找到的路径必须是具有可用容量的最短路径。 这可以通过广度优先搜索找到，其中我们对每个边缘应用1的权重。 通过显示每个增强路径可以在O（E）时间内找到O（V E2）的运行时间，每次E边缘中的至少一个变得饱和（具有最大可能流量的边缘）， 从增强路径到饱和边缘到源的距离必须比上次饱和的时间长，并且长度最多为V.该算法的另一个特性是最短增强路径的长度单调增加。 算法简介中有一个可访问的证明。（copy自百度）

☞『本质』

　　其实说白了就是优先寻找最短路的FF算法。

▎算法高效性证明

☞『引理1』

引理：令f_i表示增广i次后得到的容许流，λ^k(u,v)表示f_k中u到v的一条最短路长度，那么就有：

　　λ^k(S,v)≤λ^k+1(S,v),λ^k(v,T)≤λ^k+1(v,T)

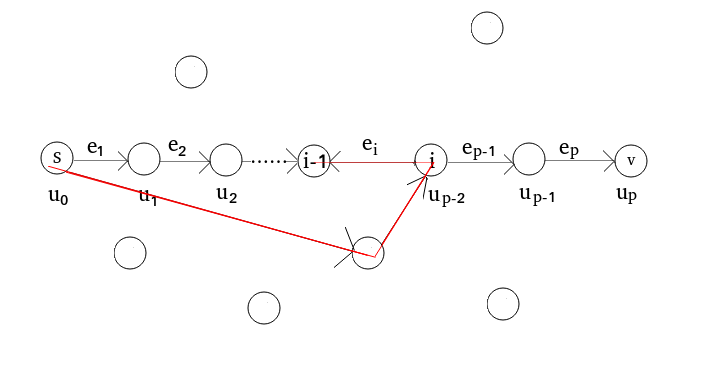
证明：

假设f_k+1中有一条从S到T的最短路为S=u₀,u₁,…,u_p-1,u_p=v，其中边记为e，e_i表示(u_i-1,u_i)的长度，图解一下是这样的：

那么这是k+1次增广的结果，那么我们继续思考k次会是怎样的。

对于每一条边e_i，都会有两种情况：

①在f_k中也是可以使用的（没有用于此次增广），那么显然有λ^k(S,u_i)≤λ^k(S,u_i-1)+1;那么i与i-1有连边，所以可能等于，因为S到ui的最短路可能是从其他点绕过来的，所以可能是小于的；

②在f_k中是不可以使用的（用于了增广），那么很显然λ^k(S,u_i-1)=λ^k(S,u_i)+1；这个不好讲，放张图自行体会吧。

综上，就有λ^k(S,v)≤λ^k+1(S,v)了。

☞『引理2』

引理：设边e在f_k变为f_k+1的增广路上，e´在f_l变为f_l+1的增广路上（k<l），那么就有：

λ^l(S,T)≥λ^k(S,T)+2

证明：假设e=(u,v)，那么显然：

λ^k(S,v)=λ^k(S,u)+1

λ^l(S,T)=λ^l(S,u)+1+λ^l(u,T)

再由引理1替换得：

λ^l(S,T)≥λ^k(S,T)+2

 ☞『算法时间复杂度分析』

若边e在f_k1,f_k2,f_k3,…中成为瓶颈（就是变化为0了），那么就必定存在f_l1,f_l2,f_l3…，满足k₁<l₁<k₂<l₂<…，且e´在f_li变为f_li+1的增广路中。

就是说e在k_i次增广时变成逆向的，在l_i次增广时变为正向的，这样k_i+1次可以继续增广。

显然，S到T的最短路在1到n-1之间，其中n是总点数，每次改变e的方向，都会导致最短路长度加2（引理2）。

如果是第k_j次增广，那么e变化的次数不可能超过2j-2次，就有：

2(2j-2)≤n-1-1（变化量小于上界减下界），把j单独移到一边去，就得到j≤（n+2）/4，由于一条边还有反向弧，所以一条边至多成为（n+2）/2次瓶颈，也就是说最多有m（n+2）/2条增广路。

这样，这个算法的时间复杂度就与权值无关了。