加权图的最小生成树、最短路径算法 - java实现
加权图相关算法
前言
本文主要介绍加权图算法中两个重要应用:最小生成树和最短路径。
求最小生成树时针对的是加权无向图,加权有向图的最小生成树算法成为“最小属树形图”问题,较为复杂,本文不做讨论。
求最短路径则是针对加权有向图,在不同限制条件下,适应不同的算法:
1. 权重非负,采用Dijkstra算法;
2. 不存在环,采用基于拓扑排序的最短路径算法,能够线性空间内解决问题;
3. 不存在负权重环,即如果存在环,环的各条边权重总和不能为负值,采用Bellman-Ford算法。
加权无向图的最小生成树
重新定义最小生成树数据结构,为更好表示,针对边也定义数据结构。
/**
* 定义加权无向图的边
*/
public class Edge implements Comparable<Edge>{
private final int v;
private final int w;
private final double weight;
public Edge(int v, int w, double weight) {
this.v = v;
this.w = w;
this.weight = weight;
}
public int either(){ return v; }
public int other(int vertex){
if(v == vertex) return w;
else return v;
}
public double weight(){ return weight; }
@Override
public int compareTo(Edge o) { return Double.compare(weight, o.weight); }
@Override
public String toString() {
return "Edge{" +
"v=" + v +
", w=" + w +
", weight=" + weight +
'}';
}
}
/**
* 定义加权无向图
*/
public class EdgeWeightedGraph {
private int V;
private int E;
private ArrayList<Edge>[] adj;
public EdgeWeightedGraph(int V){
this.V = V;
adj = (ArrayList<Edge>[]) new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
}
public EdgeWeightedGraph(Scanner scanner){
this(scanner.nextInt());
int E = scanner.nextInt();
for (int i = 0; i < E; i++) {
int v = scanner.nextInt();
int w = scanner.nextInt();
double weight = scanner.nextDouble();
Edge edge = new Edge(v, w, weight);
addEdge(edge);
}
}
public void addEdge(Edge edge){
int v = edge.either();
int w = edge.other(v);
adj[v].add(edge);
adj[w].add(edge);
E++;
}
public Iterable<Edge> adj(int v){ return adj[v]; }
public int V() { return V; }
public int E() { return E; }
public Iterable<Edge> edges(){
ArrayList<Edge> edges = new ArrayList<>();
for (int v = 0; v < V; v++) {
for (Edge edge : adj[v]) {
if(edge.other(v) > v){
edges.add(edge);
}
}
}
return edges;
}
}
/**
* 采用Prim算法求加权无向图的最小生成树
*/
public class PrimMST {
private Edge[] edgeTo; // 到达w节点的那条边
private double[] distTo; // 到达w节点的边的权重,等价于edgeTo[w].weight()
private boolean[] marked; // 标记节点是否在树中
private TreeMap<Edge, Integer> queue; // 存储未在树中的边
public PrimMST(EdgeWeightedGraph G){
edgeTo = new Edge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
queue = new TreeMap<>();
for (int i = 0; i < G.V(); i++) {
distTo[i] = Double.POSITIVE_INFINITY;
}
// 初始化,也可采用其他方式
for (Edge edge : G.adj(0)) {
queue.put(edge, edge.other(0));
if(distTo[0] > edge.weight()){
edgeTo[0] = edge;
distTo[0] = edge.weight();
}
}
while (!queue.isEmpty()){
// 从队列中找出边权重最小的边
Map.Entry<Edge, Integer> minEntry = queue.firstEntry();
queue.remove(minEntry.getKey());
visit(G, minEntry.getValue());
}
}
private void visit(EdgeWeightedGraph G, int v){
// 标记为在书中
marked[v] = true;
for (Edge edge : G.adj(v)) {
int w = edge.other(v);
if(distTo[w] > edge.weight()){
Edge pre = edgeTo[w];
edgeTo[w] = edge;
distTo[w] = edge.weight();
if(marked[w]) continue;
if(null != pre) queue.remove(pre);
queue.put(edge, w);
}
}
}
/**
* 返回最小生成树的边集合
*/
public Iterable<Edge> edges(){ return Arrays.asList(edgeTo); }
/**
* 最小生成树的权重
*/
public double weight(){
double weight = 0.0;
for (Edge edge : edgeTo) {
weight += edge.weight();
}
return weight;
}
private void print(){
for (int v = 0; v < edgeTo.length; v++) {
Edge edge = edgeTo[v];
System.out.println(v + " " + edge.other(v));
}
}
public static void main(String[] args) {
// 输入数据见附录1
EdgeWeightedGraph G = new EdgeWeightedGraph(new Scanner(System.in));
PrimMST primMST = new PrimMST(G);
// 输出结果参见附录2
System.out.println("最小生成树的边");
primMST.print();
System.out.println("树权重总和: " + primMST.weight());
}
}
加权有向图的最短路径算法
定义加权有向图
/**
* 加权有向图的边
*/
public class WeightDirectedEdge implements Comparable<WeightDirectedEdge> {
private int from;
private int to;
private double weight;
public WeightDirectedEdge(int from, int to, double weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
public int from(){ return from; }
public int to() { return to; }
public double weight(){ return weight; }
@Override
public int compareTo(WeightDirectedEdge o) { return Double.compare(weight, o.weight); }
}
/**
* 定义加权有向图
*/
public class EdgeWeightDigraph {
private int V;
private int E;
private ArrayList<WeightDirectedEdge>[] adj;
public EdgeWeightDigraph(int V){
this.V = V;
adj = (ArrayList<WeightDirectedEdge>[])new ArrayList[V];
for (int v = 0; v < V; v++) {
adj[v] = new ArrayList<>();
}
}
public EdgeWeightDigraph(Scanner scanner){
this(scanner.nextInt());
int E = scanner.nextInt();
for (int v = 0; v < E; v++) {
int from = scanner.nextInt();
int to = scanner.nextInt();
double weight = scanner.nextDouble();
addEdge(new WeightDirectedEdge(from, to, weight));
}
}
public int V() { return V; }
public int E() { return E; }
public Iterable<WeightDirectedEdge> adj(int v){ return adj[v]; }
public void addEdge(WeightDirectedEdge edge){
adj[edge.from()].add(edge);
E++;
}
}
Dijkstra算法求非负权重有向图最短路径
该算法的使用前提条件是图中不存在权重为负的边,算法的优势在于最坏情况下仍能保证ElogV的时间复杂度。
/**
* Dijkstra算法求最短路径
*/
public class DijkstraSP {
private WeightDirectedEdge[] edgeTo;
private double[] distTo;
private boolean[] marked;
private TreeSet<WeightPoint> pq;
// 定义一个权重和顶点的类,也可采用其他方式表示
private class WeightPoint implements Comparable<WeightPoint>{
private double weight;
private int v;
public WeightPoint(double weight, int v) {
this.weight = weight;
this.v = v;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
WeightPoint that = (WeightPoint) o;
return v == that.v;
}
@Override
public int hashCode() {
return Objects.hash(v);
}
@Override
public int compareTo(WeightPoint o) { return Double.compare(weight, o.weight); }
}
public DijkstraSP(EdgeWeightDigraph G, int s){
edgeTo = new WeightDirectedEdge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
pq = new TreeSet<>();
for (int v = 0; v < G.V(); v++) {
distTo[v] = Double.POSITIVE_INFINITY;
}
distTo[s] = 0.0;
pq.add(new WeightPoint(0.0, 0));
while (!pq.isEmpty()){
WeightPoint point = pq.pollFirst();
relax(G, point.v);
}
}
private void relax(EdgeWeightDigraph G, int v){
marked[v] = true;
for (WeightDirectedEdge edge : G.adj(v)) {
int w = edge.to();
if(distTo[w] > distTo[v] + edge.weight()){
pq.remove(new WeightPoint(distTo[w], w));
edgeTo[w] = edge;
distTo[w] = distTo[v] + edge.weight();
pq.add(new WeightPoint(distTo[w], w));
}
}
}
public boolean hasPathTo(int v){ return distTo[v] < Double.POSITIVE_INFINITY; }
public double distTo(int v) { return distTo[v]; }
public Iterable<WeightDirectedEdge> pathTo(int v){
if(!hasPathTo(v)) return null;
Stack<WeightDirectedEdge> stack = new Stack<>();
for (WeightDirectedEdge e=edgeTo[v]; e !=null ; e=edgeTo[e.from()])
stack.add(e);
return stack;
}
public static void main(String[] args) {
// 输入用例参见附录3
EdgeWeightDigraph G = new EdgeWeightDigraph(new Scanner(System.in));
DijkstraSP sp = new DijkstraSP(G, 0);
// 测试输出结果参见附录4
System.out.println("0顶点至各点的最短路径: ");
for (int v = 1; v < G.V(); v++) {
if (!sp.hasPathTo(v)){
System.out.println(v + " 无路径");
continue;
}
System.out.print(v + " ");
for (WeightDirectedEdge e : sp.pathTo(v)) {
System.out.print(e.from() + "->" + e.to() + " ");
}
System.out.println();
}
}
}
基于拓扑排序求无环有向图的最短路径
针对无环有向图,按照拓扑排序的顺序,依次relax顶点,既可实现最短路径。算法的优势是时间复杂度为E+V。原理为每次
relax顶点s时,所有能到达s的顶点已经被relax。具体实现略。
Bellman-Ford算法求无负权重环的最短路径
当图形含有负权重边或者环时,这时需要Bellman-Ford算法,算法限制条件是不含有负权重的环。最坏情况下的
时间复杂度是EV。算法依赖有向图的环检测算法。
/**
* 加权有向图的环检测
*/
public class WeightDigraphCycle {
private boolean[] onStack;
private boolean[] marked;
private WeightDirectedEdge[] edgeTo;
private Stack<Integer> cycle;
public WeightDigraphCycle(EdgeWeightDigraph G){
onStack = new boolean[G.V()];
marked = new boolean[G.V()];
edgeTo = new WeightDirectedEdge[G.V()];
for (int v = 0; v < G.V(); v++) {
if(!marked[v])
dfs(G, v);
}
}
private void dfs(EdgeWeightDigraph G, int v){
marked[v] = true;
onStack[v] = true;
for (WeightDirectedEdge edge : G.adj(v)) {
int w = edge.to();
if(hasCycle()) return;
else if(!marked[w]){
edgeTo[w] = edge;
dfs(G, w);
}
else if(onStack[w]){
cycle = new Stack<>();
for (int x = v; x!=w; x = edgeTo[x].from())
cycle.push(x);
cycle.push(w);
cycle.push(v);
}
}
onStack[v] = false;
}
public boolean hasCycle() { return cycle != null; }
public Stack<Integer> cycle(){ return cycle; }
}
/**
* Bellman-Ford算法
* 针对不存在负权重环的加权有向图,求最短路径
* 算法依赖有向图的环检测
*/
public class BellmanFordSP {
private double[] distTo;
private WeightDirectedEdge[] edgeTo;
private boolean[] onQ;
private TreeSet<WeightPoint> pq;
private Stack<Integer> cycle;
private int cost;
// 定义一个权重和顶点的类
private class WeightPoint implements Comparable<WeightPoint>{
private double weight; // 等价于distTo[v]
private int v;
public WeightPoint(double weight, int v) {
this.weight = weight;
this.v = v;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
WeightPoint that = (WeightPoint) o;
return v == that.v;
}
@Override
public int hashCode() {
return Objects.hash(v);
}
@Override
public int compareTo(WeightPoint o) { return Double.compare(weight, o.weight); }
}
public BellmanFordSP(EdgeWeightDigraph G, int s){
distTo = new double[G.V()];
edgeTo = new WeightDirectedEdge[G.V()];
onQ = new boolean[G.V()];
pq = new TreeSet<>();
for (int i = 0; i < G.V(); i++) {
distTo[i] = Double.POSITIVE_INFINITY;
}
distTo[s] = 0.0;
pq.add(new WeightPoint(0.0, s));
onQ[s] = true;
while (!pq.isEmpty() && !hasNagetiveCycle()){
WeightPoint weightPoint = pq.pollFirst();
relax(G, weightPoint.v);
}
}
private void relax(EdgeWeightDigraph G, int v){
onQ[v] = false;
for (WeightDirectedEdge directedEdge : G.adj(v)) {
if(hasNagetiveCycle()) return;
int w = directedEdge.to();
if(distTo[w] > distTo[v] + directedEdge.weight()){
distTo[w] = distTo[v] + directedEdge.weight();
edgeTo[w] = directedEdge;
if(!onQ[w]){
onQ[w] = true;
pq.add(new WeightPoint(directedEdge.weight(), w));
}
}
if(cost++ % G.V() == 0)
findNagetiveCycle();
}
}
private boolean hasNagetiveCycle(){ return cycle != null; }
private void findNagetiveCycle(){
int V = edgeTo.length;
EdgeWeightDigraph digraph = new EdgeWeightDigraph(V);
for (int i = 0; i < V; i++) {
if(edgeTo[i] != null){
digraph.addEdge(edgeTo[i]);
}
}
WeightDigraphCycle weightDigraphCycle = new WeightDigraphCycle(digraph);
if (weightDigraphCycle.hasCycle())
cycle = weightDigraphCycle.cycle();
}
public boolean hasPathTo(int v){ return distTo[v] < Double.POSITIVE_INFINITY; }
public Iterable<WeightDirectedEdge> pathTo(int v){
if(!hasPathTo(v)) return null;
ArrayDeque<WeightDirectedEdge> paths = new ArrayDeque<>();
for (WeightDirectedEdge e = edgeTo[v]; e!= null; e=edgeTo[e.from()]){
paths.push(e);
}
return paths;
}
public static void main(String[] args) {
// 测试输入用例参见附录5
EdgeWeightDigraph digraph = new EdgeWeightDigraph(new Scanner(System.in));
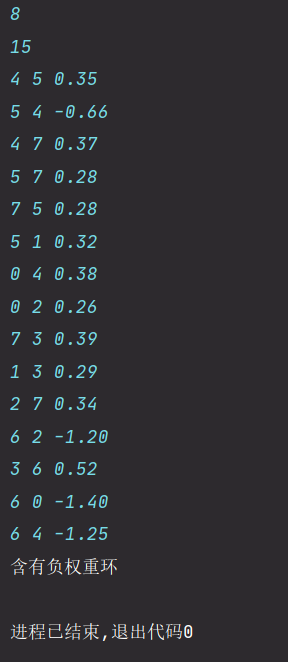
BellmanFordSP bellmanFordSP = new BellmanFordSP(digraph, 5);
// 输出用例参见附录6
if(bellmanFordSP.hasNagetiveCycle()){
System.out.println("含有负权重环");
} else {
for (int i = 1; i < digraph.V(); i++) {
System.out.print("5 到顶点 " + i + "是否有路径: " + (bellmanFordSP.hasPathTo(i) ? "是" : "否"));
if(bellmanFordSP.hasPathTo(i)){
System.out.print(", 最短路径为:");
for (WeightDirectedEdge directedEdge : bellmanFordSP.pathTo(i)) {
System.out.print(directedEdge.from() + "->" + directedEdge.to() + " ");
}
}
System.out.println();
}
}
}
}
附录1 加权无向图的输入用例

附录2 最小生成树的测试输出
最小生成树的边
0 7
1 7
2 3
3 2
4 5
5 7
6 2
7 1
树权重总和: 1.9100000000000001
附录3 Dijkstra输入用例
9
15
4 5 0.35
5 4 0.35
4 7 0.37
5 7 0.28
7 5 0.28
5 1 0.32
0 4 0.38
0 2 0.26
7 3 0.39
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52
6 0 0.58
6 4 0.93
附录4 Dijkstra输出用例
0顶点至各点的最短路径:
1 5->1 4->5 0->4
2 0->2
3 7->3 2->7 0->2
4 0->4
5 4->5 0->4
6 3->6 7->3 2->7 0->2
7 2->7 0->2
8 无路径
附录5 Bellman-Ford输入用例1
8
15
4 5 0.35
5 4 0.35
4 7 0.37
5 7 0.28
7 5 0.28
5 1 0.32
0 4 0.38
0 2 0.26
7 3 0.39
1 3 0.29
2 7 0.34
6 2 -1.20
3 6 0.52
6 0 -1.40
6 4 -1.25
附录6 Bellman-Ford输出用例1
5 到顶点 1是否有路径: 是, 最短路径为:5->1
5 到顶点 2是否有路径: 是, 最短路径为:5->1 1->3 3->6 6->2
5 到顶点 3是否有路径: 是, 最短路径为:5->1 1->3
5 到顶点 4是否有路径: 是, 最短路径为:5->1 1->3 3->6 6->4
5 到顶点 5是否有路径: 是, 最短路径为:
5 到顶点 6是否有路径: 是, 最短路径为:5->1 1->3 3->6
5 到顶点 7是否有路径: 是, 最短路径为:5->1 1->3 3->6 6->4 4->7
附录7 Bellman-Ford输入用例2,含有负权重环

附录8 Bellman-Ford输出用例2,含有负权重环
加权图的最小生成树、最短路径算法 - java实现的更多相关文章
- 无向图的最短路径算法JAVA实现
一,问题描述 给出一个无向图,指定无向图中某个顶点作为源点.求出图中所有顶点到源点的最短路径. 无向图的最短路径其实是源点到该顶点的最少边的数目. 本文假设图的信息保存在文件中,通过读取文件来构造图. ...
- 无向图的最短路径算法JAVA实现(转)
一,问题描述 给出一个无向图,指定无向图中某个顶点作为源点.求出图中所有顶点到源点的最短路径. 无向图的最短路径其实是源点到该顶点的最少边的数目. 本文假设图的信息保存在文件中,通过读取文件来构造图. ...
- 带权图的最短路径算法(Dijkstra)实现
一,介绍 本文实现带权图的最短路径算法.给定图中一个顶点,求解该顶点到图中所有其他顶点的最短路径 以及 最短路径的长度.在决定写这篇文章之前,在网上找了很多关于Dijkstra算法实现,但大部分是不带 ...
- 最短路径算法之Dijkstra算法(java实现)
前言 Dijkstra算法是最短路径算法中为人熟知的一种,是单起点全路径算法.该算法被称为是“贪心算法”的成功典范.本文接下来将尝试以最通俗的语言来介绍这个伟大的算法,并赋予java实现代码. 一.知 ...
- Java邻接表表示加权有向图,附dijkstra最短路径算法
从A到B,有多条路线,要找出最短路线,应该用哪种数据结构来存储这些数据. 这不是显然的考查图论的相关知识了么, 1.图的两种表示方式: 邻接矩阵:二维数组搞定. 邻接表:Map<Vertext, ...
- 最小生成树(prime算法 & kruskal算法)和 最短路径算法(floyd算法 & dijkstra算法)
一.主要内容: 介绍图论中两大经典问题:最小生成树问题以及最短路径问题,以及给出解决每个问题的两种不同算法. 其中最小生成树问题可参考以下题目: 题目1012:畅通工程 http://ac.jobdu ...
- 有向图的拓扑排序算法JAVA实现
一,问题描述 给定一个有向图G=(V,E),将之进行拓扑排序,如果图有环,则提示异常. 要想实现图的算法,如拓扑排序.最短路径……并运行看输出结果,首先就得构造一个图.由于构造图的方式有很多种,这里假 ...
- Dijkstra最短路径算法[贪心]
Dijkstra算法的标记和结构与prim算法的用法十分相似.它们两者都会从余下顶点的优先队列中选择下一个顶点来构造一颗扩展树.但千万不要把它们混淆了.它们解决的是不同的问题,因此,所操作的优先级也是 ...
- 最短路径算法-Dijkstra算法的应用之单词转换(词梯问题)(转)
一,问题描述 在英文单词表中,有一些单词非常相似,它们可以通过只变换一个字符而得到另一个单词.比如:hive-->five:wine-->line:line-->nine:nine- ...
随机推荐
- 2020.5.24 第四篇 Scrum冲刺博客
Team:银河超级无敌舰队 Project:招新通 项目冲刺集合贴:链接 目录 一.每日站立会议 1.1 会议照片 1.2 项目完成情况 二.项目燃尽图 三.签入记录 3.1 代码/文档签入记录 3. ...
- 区块链入门到实战(32)之Solidity – 代码注释
Solidity 支持c风格和c++风格的注释. //之后到行尾的文本,都被看作注释,编译器忽略此内容 /* 与 */ 之间的文本被看作注释, 编译器忽略此内容 示例 注释示例. function g ...
- RCON 服务器命令协议
介绍 编辑 RCON是一种允许服务器管理员远程执行Minecraft命令的协议.在1.9pre4中引入,它基本上是Minecraft的Source RCON协议的实现. 格式 编辑 响应将使用您发送的 ...
- javascript 查找属性的过程
当执行 一个对象赋值操作的时候 js引擎会怎样处理呢??? 例如 有个foo对象 ,要进行这个操作 foo.a=2 1, 首先会在foo对象中查找,如果不存在a属性,就会去原型链上面找,如果原 ...
- 关于idea中SpringBoot启动失败的坑
很多时候你新建了Maven 或者SpringBoot 工程,激动的点了主启动类,你就发现了下面的错误 Error starting Tomcat context. Exception: org.spr ...
- 为什么 list(range) 比 [i for i in range()] 快?
为什么 list(range) 比 [i for i in range()] 快? t0 = time.time() list(range(100000)) print(time.time()-t0) ...
- Spine学习九 - 冰冻效果
想象这样一个效果,一个人被冰霜攻击命中,然后这个人整个就被冰冻了,那么spine动画要如何实现这个效果呢? 1.首先需要一个Spine动画,这个动画应该是相对静止的,因为人物已经被冰冻了,那么这个人儿 ...
- 模拟CMOS集成电路 课后习题总结(2.1)
前几天开始自学拉扎维的模设教材,看之前浏览了EETOP论坛里面好多大神们对这本书的看法,当然也有人在抱怨,比如冒出“太科幻”.“一年才看完”之类恐怖的修饰语句,因此在开始看的时候就对此书充满了“敬畏” ...
- CC2530的ADC采集外部电压
初窥ZIGBEE 要在zigbee的组网中加入烟雾传感器的模块,所以需要用到cc2530的ADC对传感器输出的模拟信号进行采样.下面是自己对实现用CC2530的ADC采集外部电压的程序过程. 以下是A ...
- 18_Python常用的模块中的某个方法
1.imp模块==========>重新加载已加载过的模块方法 import imp imp.reload(mymod) # 重新加载已经加载过的mymod模块 2.ctypes模块====== ...
