4.23 子串 AC自动机 概率期望 高斯消元

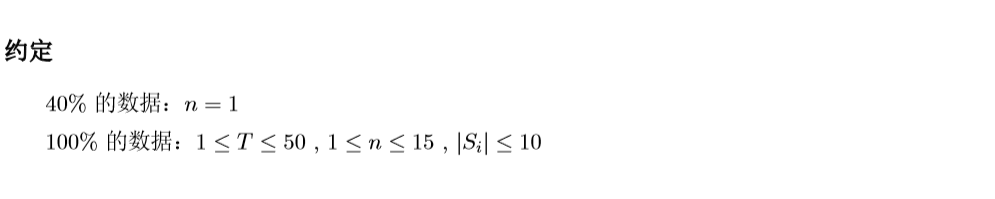
考虑40分。

设出状态 f[i]表示匹配到了i位还有多少期望长度能停止。可以发现这个状态有环 需要高斯消元。

提供一种比较简单的方法：由于期望的线性可加性 可以设状态f[i]表示由匹配到i到匹配到i+1需要的期望长度。

需要预处理前缀和和KMP的nex数组来辅助转移。

if(n==1)
		{
			gc(a);
			len=strlen(a+1);
			ll j=0;
			memset(nex,0,sizeof(nex));
			rep(2,len,i)
			{
				while(j&&a[i]!=a[j+1])j=nex[j];
				if(a[i]==a[j+1])++j;
				nex[i]=j;
			}
			rep(0,len-1,i)
			{
				f[i]=1;
				for(ll j=0;j<=25;++j)
				{
					if(a[i+1]-'a'!=j)
					{
						ll w=i;
						while(w&&a[w+1]-'a'!=j)w=nex[w];
						if(a[w+1]-'a'!=j){if(i)f[i]=(f[i]+sum[i-1])%mod;}
						else f[i]=(f[i]+sum[i-1]-sum[w])%mod;
						++f[i];
					}
				}
				if(i>=1)sum[i]=(sum[i-1]+f[i])%mod;
				else sum[i]=f[i];
			}
			ll ans=0;
			rep(0,len-1,i)ans=(ans+f[i])%mod;
			putl(ans);
		}

考虑正解。

容易想到建立出AC自动机 在trie图上跑。

易设状态f[i]表示到达i这个点的期望长度。

遗憾的是 这个玩意根本不能转移。或者说转移必然存在问题 比如 \(f_i=\sum_{v\in fa[i],vis[v]\neq 1}\frac{f_v+1}{26}\)

vis数组表示v是否是终止节点。

容易想错的是 v转移到i的概率确实是1/26 但是i从v处转移的概率却不一定是1/26.

可能到达v的次数有很多次 每次概率都是1/26不过这个次数并没有被统计到 这是关键点。

而且据EI dalao所说 v转移到i的所有的概率和不为1 而且 E[x/y] 通常不等于 E[x]/E[y]。

总之 当做概率出现的问题吧.

考虑由最开始的状态倒推期望 设f[i]表示到达i这个节点还需要多少长度才能停止。

容易 发现转移 \(f_i=1+\sum_{v\in son[i]}\frac{f_v}{26}\)

可以发现这个状态的转移概率确实1/26.

而且这个状态带环。所以高斯消元即可。

const ll MAXN=12,maxn=210;
ll T,n,len,cnt;
inline ll ksm(ll b,ll p){ll cnt=1;while(p){if(p&1)cnt=(ll)cnt*b%mod;b=(ll)b*b%mod;p=p>>1;}return cnt;}
char a[maxn];
ll nex[maxn],q[maxn];
ll b[maxn][maxn];
ll f[maxn],sum[maxn];//f[i]表示由长度i到长度i+1的期望.
struct AC
{
	ll s;
	ll fail;
	ll ch[26];
}t[maxn];
inline ll get_new()
{
	++cnt;
	t[cnt]=t[200];
	return cnt;
}
inline void insert(char *a)
{
	ll p=0;
	ll len=strlen(a+1);
	rep(1,len,i)
	{
		ll w=a[i]-'a';
		if(!t[p].ch[w])t[p].ch[w]=get_new();
		p=t[p].ch[w];
	}
	t[p].s=1;
}
inline void get_fail()
{
	ll l=0,r=0;
	rep(0,25,i)if(t[0].ch[i])q[++r]=t[0].ch[i];
	while(++l<=r)
	{
		ll x=q[l];
		rep(0,25,i)
		{
			ll tn=t[x].ch[i];
			if(tn)fail(tn)=t[fail(x)].ch[i],q[++r]=tn;
			else t[x].ch[i]=t[fail(x)].ch[i];
		}
	}
	rep(1,r,i)t[q[i]].s|=t[fail(q[i])].s;
}
inline void GAUSS()
{
	rep(0,cnt,i)
	{
		ll p=i;
		rep(i+1,cnt,j)if(abs(b[j][i])>abs(b[i][i]))p=j;
		if(p!=i){rep(0,cnt,k)swap(b[i][k],b[p][k]);swap(f[i],f[p]);}
		ll d=ksm(b[i][i],mod-2);
		rep(0,cnt,j)
		{
			if(i==j)continue;
			ll ww=d*b[j][i]%mod;
			rep(0,cnt,k)b[j][k]=(b[j][k]-b[i][k]*ww)%mod;
			f[j]=(f[j]-f[i]*ww)%mod;
		}
	}
	rep(0,cnt,i)f[i]=f[i]*ksm(b[i][i],mod-2)%mod;
}
signed main()
{
	freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	//freopen("substring.in","r",stdin);
	//freopen("substring.out","w",stdout);
	gt(T);
	while(T--)
	{
		gt(n);
		{
			cnt=0;t[0]=t[200];
			rep(1,n,i)gc(a),insert(a);
			get_fail();
			//构建矩阵.
			ll ww=ksm(26,mod-2);
			memset(f,0,sizeof(f));
			memset(b,0,sizeof(b));
			rep(0,cnt,i)
			{
				b[i][i]=1;
				if(t[i].s)continue;
				rep(0,25,j)
				{
					int tn=t[i].ch[j];
					b[i][tn]=(b[i][tn]-ww)%mod;
				}
				++f[i];
			}
			/*rep(0,cnt,i)
			{
				rep(0,cnt,j)cout<<(b[i][j]+mod)%mod<<' ';
				cout<<f[i]<<endl;
			}*/
			GAUSS();
			/*rep(0,cnt,i)
			{
				rep(0,cnt,j)cout<<b[i][j]<<' ';
				cout<<f[i]<<endl;
			}*/
			//ll ans=0;
			//rep(1,cnt,i)if(t[i].s)ans=(ans+f[i])%mod;
			//rep(0,cnt,i)putl((f[i]+mod)%mod);
			putl((f[0]+mod)%mod);
		}
	}
	return 0;
}