AcWing 294. 计算重复

暴力

其实这题的暴力就是个模拟。暴力扫一遍 \(conn(s_1, n_1)\)，若出现了 \(res\) 个 \(s_2\)。

答案就是 \(\lfloor res / n1 \rfloor\)。

时间复杂度 \(O(T(|s_1|n1))\)。

算法1：考虑匹配一个 s1 所需的最小字符数

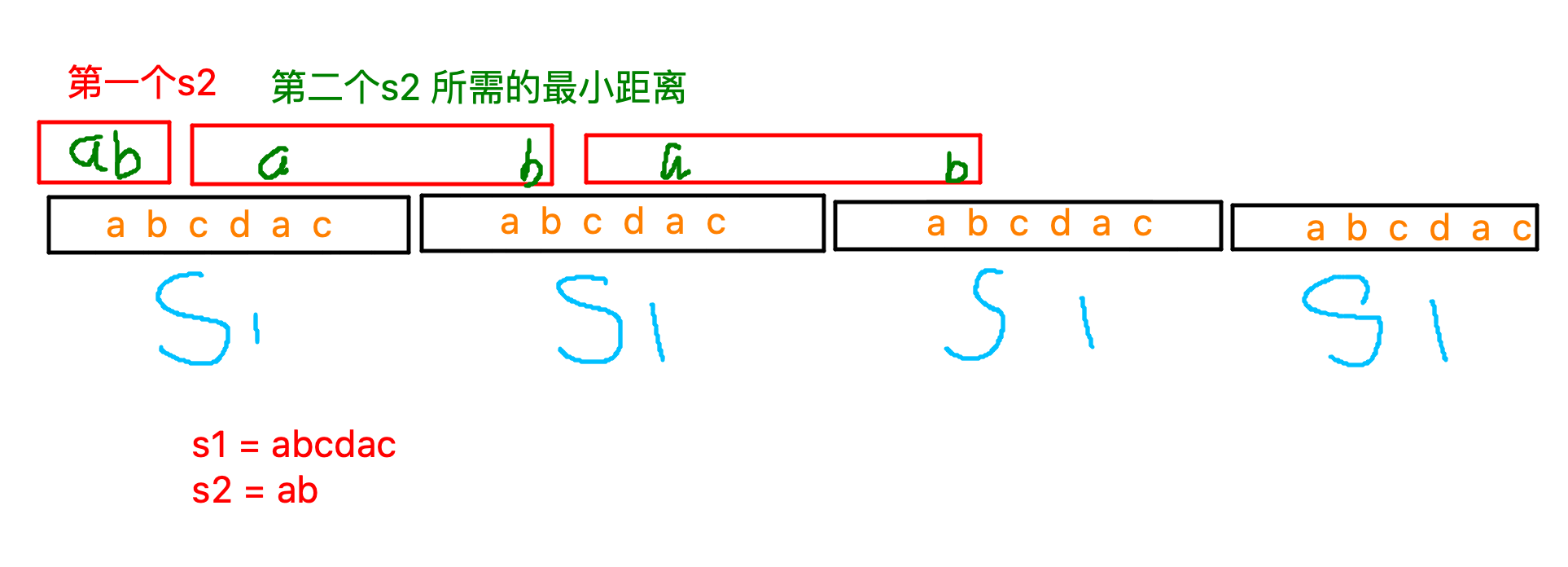
考虑字符串是一直循环的，每走完一个 \(s_2\)，他会从一个位置重新开始匹配。我们考虑预处理出对于从 \(0\) ~ \(|s1|- 1\) 这个下标 \(i\) 开始，匹配一个 \(s_2\) 所需最小的字符数，设其为 \(f[i]\)。

那么我们就不需要把整个 \(conn(s_1, n_1)\) 搞出来了，可以搞一个变量 \(p = 0\) 表示当前走过的字符数，设出现的 \(s2\) 个数 \(res = 0\)，循环执行：

如果 \(p + f[p \% |s1|] <= n1 *|s1|\)，就 \(p += f[p \% |s1|], ans++\)。形象理解就是如果还能匹配一个 \(s2\)，并且不超过限制，我就再过一个 \(s_2\)，知道上述条件不符合时停止。

考虑最坏时答案是 \(|s_1| * n1 / |s2|\)。

所以 时间复杂度 \(O(T(|s_1| * n1 / |s2|))\)。最坏情况下和暴力一样的，想了那么久你 tm 跟暴力还一样。。

倍增

刚才的跳的过程可以描述为：

• 能跳就跳
• 对于每个 \(p\) ，有唯一的后继 \(p + f[p \% |s1|]\)

这不就是明显的可以倍增优化吗？

设 \(dp[i][j]\) 为\(s_1\)循环节从下标 \(i\) 出发，匹配 \(2 ^ j\) 个 \(s_2\) 串所需的最小字符数。

初始状态：\(dp[i][0] = f[i]\)

状态转移：\(dp[i][j] = dp[i][j - 1] + dp[(i + dp[i][j - 1]) \% |s_1|][j - 1]\)，就是用两个 \(2 ^{j - 1}\) 拼出 \(2 ^ j\)。

跳的时候就用倍增模板就行了：

初始设 \(p = 0, res = 0\)，从大到小枚举 \(j\)：

• 如果 \(p + f[p \% |s_1|][j] <= n_1 *|s_1|\)，就 \(p += f[p \% |s_1|][j], ans += 2 ^ j\)。

时间复杂度

在理论最坏情况下，貌似预处理是 \(O(|s| ^ 3)\) 的，因为没说只有小写字母，所以考虑构造如下数据：

abcdefghijklmnopqrstuvwxyz......(连续不一样的100个字符)
......zyxwvutsrqponmlkjihgfedcba

那么从 \(a\)，第一个 \(s2\) 的最后才匹配到第二个字符，要匹配 \(|s_1| * |s_2| - |s_2| + 1\) 个字符才行

从 \(b\) 字符出发，要匹配 \(|s_1| * |s_2| - |s_2| + 0\) 个字符才行

...

这样，对于每个 \(i \in [0, |s_1|)\)，他会循环 $ (|s_1| - 1) * |s_2| + 2 - i$。总的就是 \(s_1 * ((|s_1|) * |s_2| + 2) - \frac{|s_1| - 1 * |s_1|}{2}\)

\(O(T(|s_1| ^ 2|s_2| + log_{|s_1| * n_1 / |s_2|}))\)。大概最坏情况 \(O(1000000T)\) 左右。

跑的已经很快了 \(13ms\)

\(Tips：\)此题输入比较毒瘤，建议用 \(cin\)。因为如果用 \(scanf\) 貌似最后有个换行如果用 \(\not= EOF\) 会再算一组数据...

或者可以采取一种奇妙的方式，\(scanf()\) 这个玩意会返回成功读入变量的数量，你可以判断是否读满了四个变量...

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 105;
char s1[N], s2[N];
int n1, n2, len1, len2, L, f[N][27];
int main() {
    while(scanf("%s %d\n%s %d", s2, &n2, s1, &n1) == 4) {
        memset(f, 0, sizeof f);
        len1 = strlen(s1), len2 = strlen(s2), L = log2(len1 * n1 / len2);
        for (int i = 0; i < len1; i++)
            for (int j = 0; f[i][0] <= len1 * len2 && j < len2; f[i][0]++)
                if(s2[j] == s1[(i + f[i][0]) % len1]) j++;
        if (f[0][0] > len1 * len2) { puts("0"); continue; }
        for (int j = 1; j <= L; j++)
            for (int i = 0; i < len1; i++)
                f[i][j] = f[i][j - 1] + f[(i + f[i][j - 1]) % len1][j - 1];
        int p = 0, ans = 0;
        for (int i = L; i >= 0; i--)
            if(p + f[p % len1][i] <= len1 * n1) p += f[p % len1][i], ans += 1 << i;
        printf("%d\n", ans / n2);
    }
    return 0;
}

算法2 考虑经过一个 s2 匹配的 s1 字符数

字符串匹配这个东西很玄妙，重新阅读这句话：

考虑字符串是一直循环的，每走完一个 \(s_2\)，他会从一个位置重新开始匹配。

那么，我们考虑预处理：

• \(f[i]\) 为已经匹配到 \(s_2\) 的第 \(i\) 位，再走完一个 \(s_1\)，能新匹配 \(s_2\) 的字符数。

显然，这个东西我们也可以用倍增优化：

设 \(dp[i][j]\) 为已经匹配到 \(s_2\) 的第 \(i\) 位，再走完 \(2 ^ j\) 个 \(s_1\)，能新匹配 \(s_2\) 的字符数。

初始状态：\(dp[i][0] = f[i]\)

状态转移：\(dp[i][j] = dp[i][j - 1] + dp[(i + dp[i][j - 1]) \% |s_2|][j - 1]\)，就是用两个 \(2 ^{j - 1}\) 的\(s_2\)拼出 \(2 ^ j\)。

最终的答案求解，只需维护一个指针 \(p\)，枚举 $n_1 $的对应二进制位 \(i\)，如果为 \(1\)，就对应跳 $f[p % |s2|][i] $ 步即可。

时间复杂度

\(O(|s_1| * |s_2| + log_2n_1)\) 跑的飞快 \(3ms\)

即使字符串长度出到 $ <= 1000$ ，\(n_1, n_2\) 到 \(long\ long\) 范围也能解决。

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 105;
char s1[N], s2[N];
int n1, n2, len1, len2, L, f[N][20];
int main() {
    while(scanf("%s %d\n%s %d", s2, &n2, s1, &n1) == 4) {
        memset(f, 0, sizeof f);
        len1 = strlen(s1), len2 = strlen(s2), L = log2(n1);
        for (int i = 0; i < len2; i++)
            for (int j = 0; j < len1; j++)
                if(s2[(i + f[i][0]) % len2] == s1[j]) f[i][0]++;
        if (!f[0][0]) { puts("0"); continue; }
        for (int j = 1; j <= L; j++)
            for (int i = 0; i < len2; i++)
                f[i][j] = f[i][j - 1] + f[(i + f[i][j - 1]) % len2][j - 1];
        int p = 0, ans = 0;
        for (int i = L; i >= 0; i--)
            if(n1 >> i & 1) ans += f[p % len2][i], p += f[p % len2][i];
        printf("%d\n", ans / len2 / n2);
    }
    return 0;
}

总结：

• 算法 \(1\) 的步长是我们的答案，倍增\(dp\)数组的具体数值是限制我们的字符，我们不知道步长，但我们知道限制。

• 算法 2 的步长是我们已知的 \(n_1\) 个字符串，倍增数组的具体数值是我们的答案（匹配了多少个字符），我们知道步长，按位枚举 \(n_1\) 下的二进制串即可。

• 两个东西是互逆的，但是反过来，时间复杂度却有神一般的提升，比较有趣。