朋友HDU - 5963 (思维题) 三种方法

传送门

题目描述

输入

输出

样例输入

Sample Input

样例输出

Boys win!
Girls win!
Girls win!
Boys win!
Girls win!
Boys win!
Boys win!
Girls win!
Girls win!
Boys win!
Girls win! 

Sample Output

分析

这道题我们首先想到的就是模拟，但是40000的数据显然是太大了，肯定会超时

那么我们来模拟一下第一个样例

这是刚开始建好的边，建完边后我们发现这棵树没有能够修改的节点

所以我们对于第一个询问0 1显然要输出 Boys win!

接下来是一个修改边的的操作 1 2 1 1

修改完后就变成了下面这样

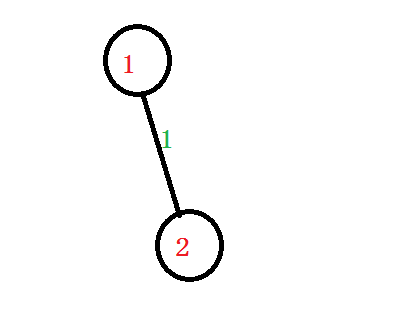
接下来又是一个询问操作0 2

我们发现在girls把（1，2）的边权修改为0后，boys不能再进行操作

所以很显然 Girls win!

第一个样例我们的模拟就结束了

是不是什么规律也没有看出来的，没有关系，我们再来第二组

（提示：注意观察与根节点相邻的边）

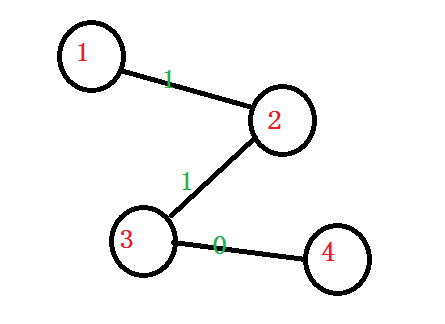
首先上来的就是四个询问，分别是1、2、3、4节点作为根节点

当1作为根节点时，操作如下图

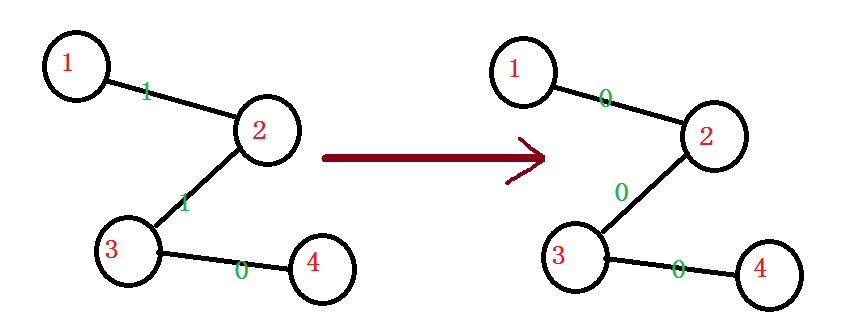
我们发现，与根节点相邻的边的权值一开始为1，经过一次操作后变成了0，这时操作结束 Girls win! 

当2为根节点时

我们发现，与根节点相邻的边有两个，权值一开始都为1，经过两次次操作后变成了0，这时操作结束 Boys win!

当3为根节点时

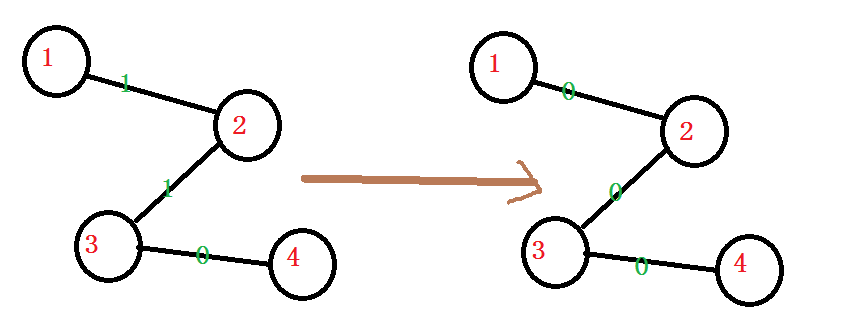
我们发现，与根节点相邻的边有两个，一个为1，一个为0，经过一次操作后1的那个变成了0，这时操作结束 Girls win!

当4为根节点时（画图好难用）

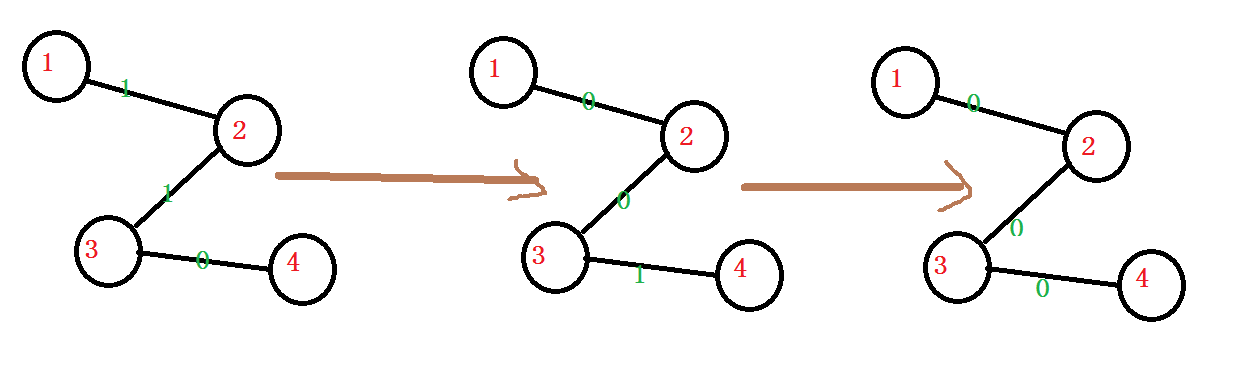
我们发现，与根节点相邻的边的权值一开始为0，经过两次操作后从0变为1又变为0，这时操作结束 Boys win!

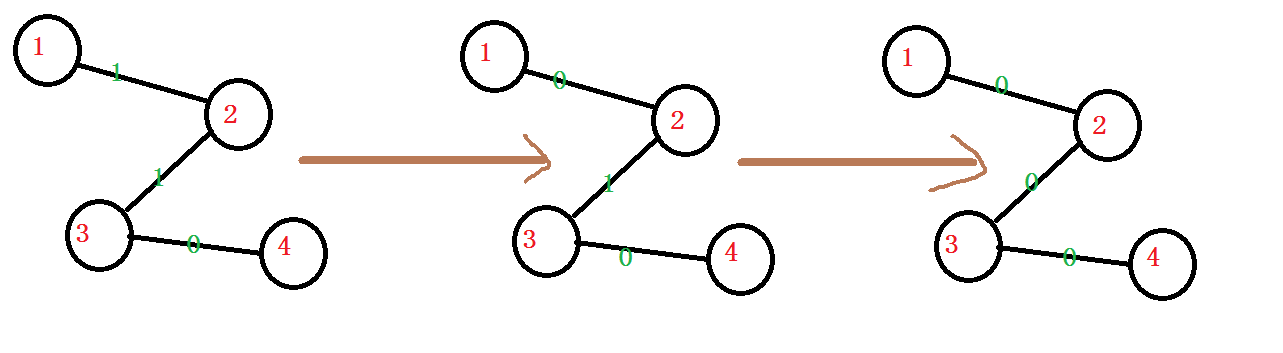
下面是一个修改边权的操作 1 2 1 0

修改完后，就成了这样

当1为根节点时

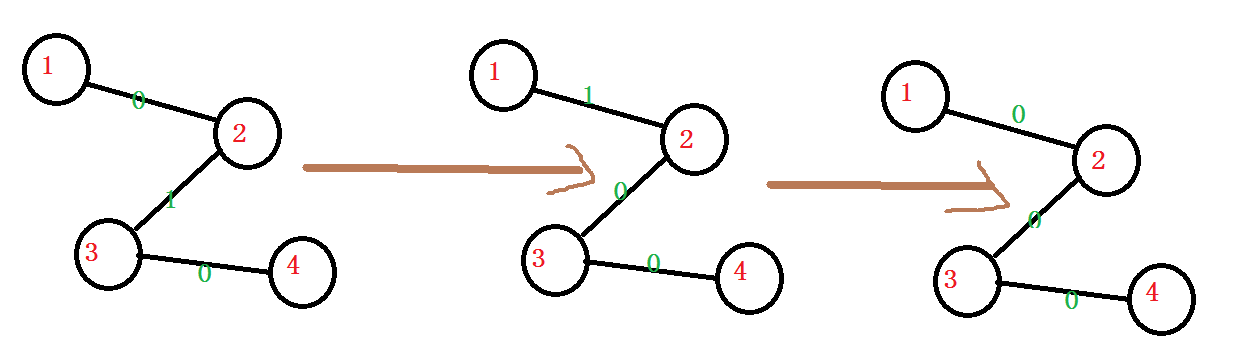
我们发现，与根节点相邻的边的权值一开始为0，经过两次操作后从0变为1又变为0，这时操作结束 Boys win!

当2为根节点时

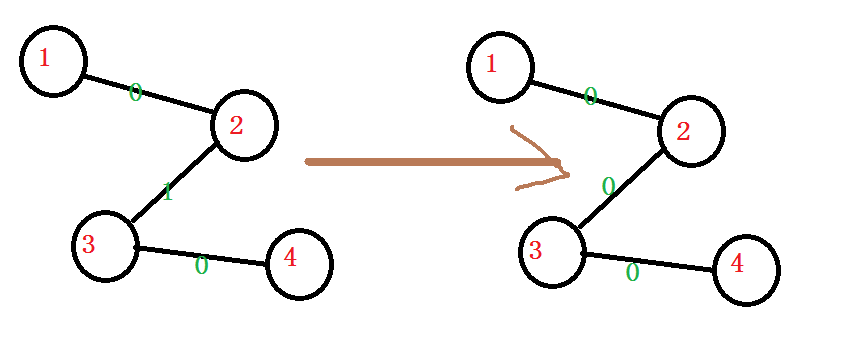
我们发现，与根节点相邻的边有两个，一个为1，一个为0，经过一次操作后1的那个变成了0，这时操作结束 Girls win!

当3为根节点时

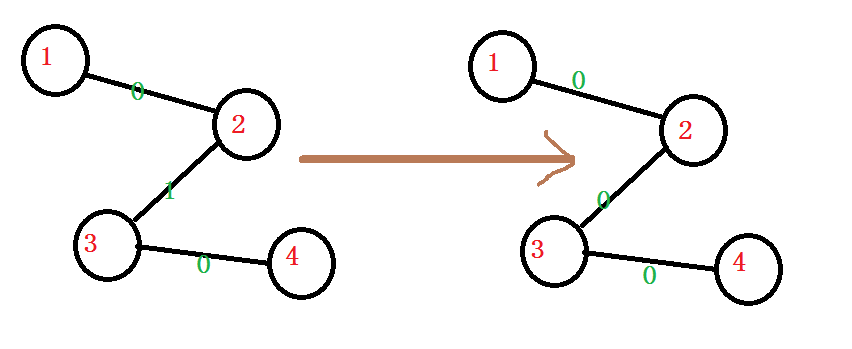
我们发现，与根节点相邻的边有两个，一个为1，一个为0，经过一次操作后1的那个变成了0，这时操作结束 Girls win!

最后又是一个修改边权的操作，我们就不再模拟

通过以上的模拟，我们可以发现什么呢？

1、操作奇数次，girls win，操作偶数次boys win（是不是很显然）

2、如果根节点只有一条边相连，那么如果这条边的边权为1，需要操作奇数次才能把它变成0，因为你的每一次操作都会对它产生影响，而且你无论后面操作多少次，最终还是要把它变为0，根据第一条性质，girls win

如果边权是0呢，就和上面相反，boys win

3、如果有多条边呢，我们就把每一条边上的操作次数累加，再根据性质1判断

方法一

听到这里，你是不是很激动呢，当给出一个根节点时，我们只需要把与它相邻的边的边权加和，再判断奇偶性就可以了

这里要注意的是，修改边的操作不一定修改成与原来相反的价值，有可能原来价值为1，修改后还为1

代码

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 #include<cmath>
 #include<ctime>
 using namespace std;
 const int maxn=;
 struct asd{
     int from,to,next,val;
 }b[maxn];
 int head[maxn],tot=;
 void ad(int aa,int bb,int cc){
     b[tot].from=aa;
     b[tot].to=bb;
     b[tot].next=head[aa];
     b[tot].val=cc;
     head[aa]=tot++;
 }
 int du[maxn];
 int main(){
     int t;
     scanf("%d",&t);
     while(t--){
         memset(head,-,sizeof(head));
         memset(&b,,sizeof(struct asd));
         memset(du,,sizeof(du));
         tot=;
         int n,m;
         scanf("%d%d",&n,&m);
         for(int i=;i<n;i++){
             int aa,bb,cc;
             scanf("%d%d%d",&aa,&bb,&cc);
             ad(aa,bb,cc);
             ad(bb,aa,cc);
             du[aa]+=cc;
             du[bb]+=cc;
         }
         while(m--){
             int cc;
             scanf("%d",&cc);
             if(cc==){
                 int aa;
                 scanf("%d",&aa);
                 int ans=du[aa];
                 if(ans%==) printf("Boys win!\n");
                 else printf("Girls win!\n");
             } else {
                 int aa,bb,cc;
                 scanf("%d%d%d",&aa,&bb,&cc);
                 for(int i=head[aa];i!=-;i=b[i].next){
                     int u=b[i].to;
                     if(bb==u && b[i].val!=cc){
                         b[i].val=cc;
                         b[i^].val=cc;
                         if(cc==){
                             du[aa]++;
                             du[bb]++;
                         } else {
                             du[aa]--;
                             du[bb]--;
                         }
                         break;
                     }
                     if(bb==u) break;
                 }
             }
         }
     }
     return ;
 }

普通枚举

写完后，我们把它交上去，发现过了，时间消耗还不多

但是我们细细一想会发现，这种做法的时间效率不能保证，我们完全可以造一组数据将它卡成n^2

比如下面这样

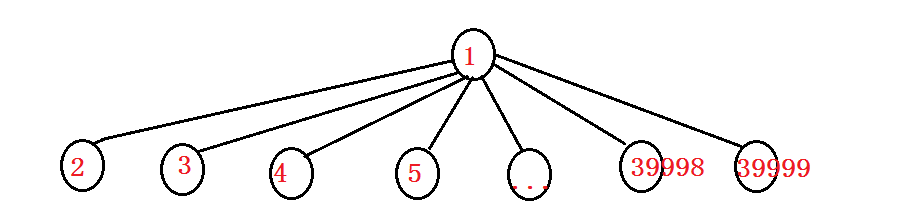
m,n小于40000，我们完全可以按照上面那样建边，然后来39999次修改操作

最后再来一次询问

而且题目中最多会给出5组数据

那么耗时就是5*40000*40000，显然会T（后面会有样例，大家可以试一下）

方法二

既然如此，那我们就要考虑怎么省去遍历边的操作

题目中只给出了0，1两种值

所以，联系我们最近学过的内容

没错，就是bitset

代码

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 #include<cmath>
 #include<bitset>
 #include<ctime>
 using namespace std;
 bitset<> bit[];
 int du[];
 int main(){
     int t;
     scanf("%d",&t);
     while(t--){
         memset(du,,sizeof(du));
         for(int i=;i<;i++){
             bit[i].reset();
         }
         int n,m;
         scanf("%d%d",&n,&m);
         for(int i=;i<n;i++){
             int aa,bb,cc;
             scanf("%d%d%d",&aa,&bb,&cc);
             if(cc==) bit[aa][bb]=bit[bb][aa]=;
             du[aa]+=cc,du[bb]+=cc;
         }
         while(m--){
             int cc;
             scanf("%d",&cc);
             if(cc==){
                 int aa;
                 scanf("%d",&aa);
                 int ans=du[aa];
                 if(ans%==) printf("Boys win!\n");
                 else printf("Girls win!\n");
             } else {
                 int aa,bb,cc;
                 scanf("%d%d%d",&aa,&bb,&cc);
                 if(bit[aa][bb]!=cc){
                     if(cc==){
                         bit[aa][bb]=bit[bb][aa]=;
                         du[aa]++,du[bb]++;
                     } else {
                         bit[aa][bb]=bit[bb][aa]=;
                         du[aa]--,du[bb]--;
                     }
                 }
             }
         }
     }
     return ;
 }

bitset

但是很遗憾内存开不下

虽然bitset很优秀，只占一个二进制位，但是题目中的内存限制为65536 kB

最多可以开一维的bitset数组65536*1024*8=536870912（5亿多，是不是很强大）

但因为是二维数组，我们开方后就只有23000了，只能达到原题数据的一半左右

如果我们开40000*40000显然会M掉

如果开23000*23000呢，会RE，因为下标访问bitset数组并不会检查越界

而且因为数组过大，你不可能每组数据都重新开一个bitset数组，所以你要初始化，但初始化就要花费几百毫秒

方法三

这时，优秀的解法该出现了

是什么呢？

答案就是map+pair

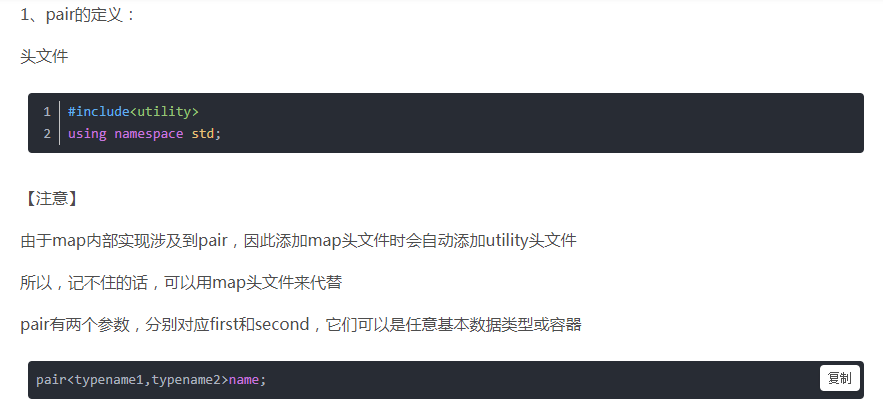
map的用法大家应该都很熟悉了，我们就简单讲一下pair吧

摘自百度百科：

 定义：c++中的结构模板，定义在头文件<utility>中，提供一个包含2个数据成员的结构体模板。继承与_Pair_base结构体模板。通过first，second访问2个成员，有 operator= 和 swap 方法。

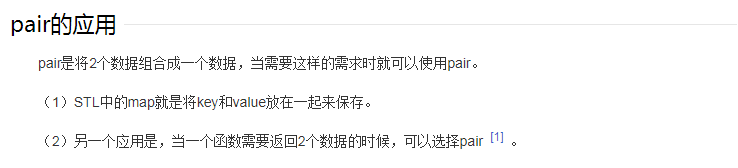
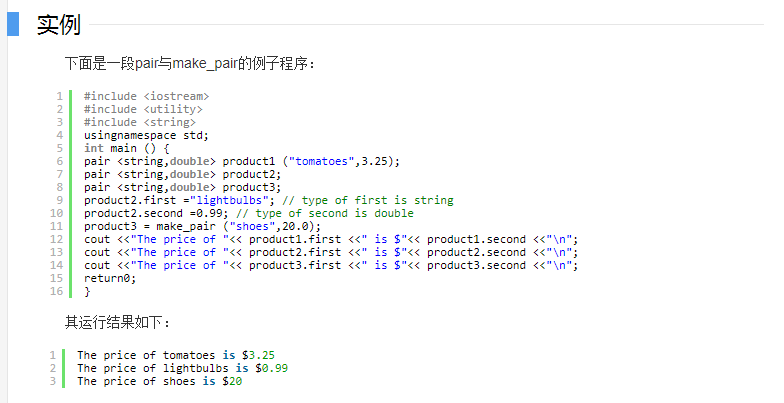
以下内容摘自：https://blog.csdn.net/qq_42232118/article/details/82078854

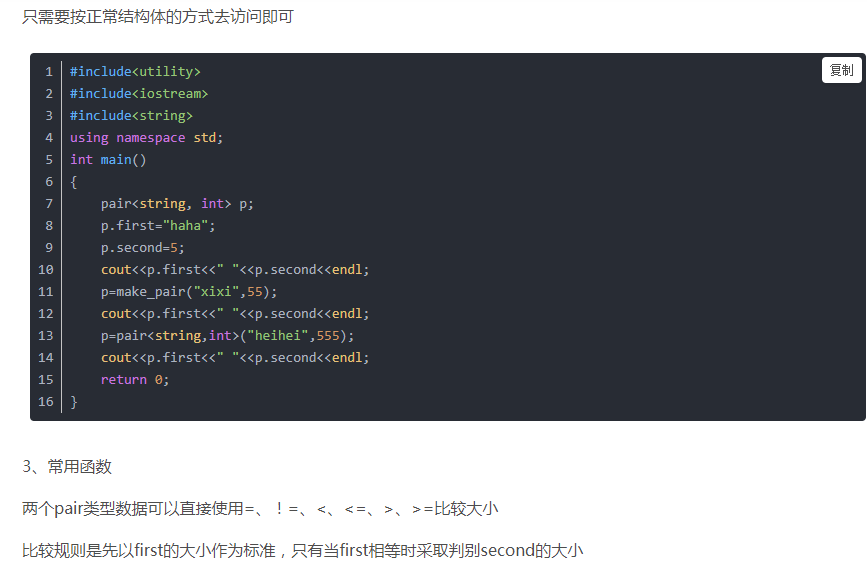
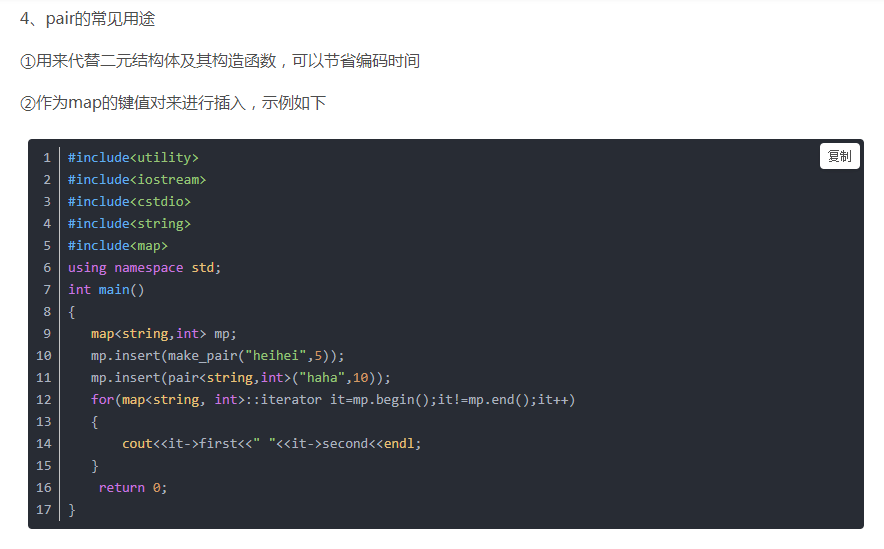
其实，这里pair的作用就是把两个元素整合在一起

那么这个算法优秀在哪里呢？

map查询元素的复杂度为O（logn）,而枚举的话复杂度是随机的，幸运的话，你一次就可以查询完，但是遇上特殊情况的话，你会被卡掉

代码

 #include<cstdio>
 #include<cstring>
 #include<map>
 #include<utility>
 #include<ctime>
 using namespace std;
 int deg[];
 map<pair<int,int>,int> amap;
 int main(){
     int t,n,m,x,y,z,id,j;
     scanf("%d",&t);
     while(t--){
         memset(deg,,sizeof(deg));
         amap.clear();
         scanf("%d%d",&n,&m);
         for(int i=;i<n;i++){
             scanf("%d%d%d",&x,&y,&z);
             if(x>y){int te=x;x=y;y=te;}  //统一顺序这样方便后期查找
             amap[make_pair(x,y)]=z;
             if(z==){
                 deg[x]++;
                 deg[y]++;
             }
         }
         for(int i=;i<m;i++){
             scanf("%d",&id);
             if(id==){
                 scanf("%d",&x);
                 if(deg[x]%) printf("Girls win!\n");
                 else printf("Boys win!\n");
             }
             else{
                 scanf("%d%d%d",&x,&y,&z);
                 if(x>y){int te=x;x=y;y=te;}
                 if(amap[make_pair(x,y)]!=z){
                     if(z==){
                         amap[make_pair(x,y)]=;
                         deg[x]--;
                         deg[y]--;
                     }
                     else{
                         amap[make_pair(x,y)]=;
                         deg[x]++;
                         deg[y]++;
                     }
                 }
             }
         }
     }
     return ;
 }

map优化

比较

这是一组符合题目要求的极端样例

样例太大，插不上，就放一个生成数据的代码吧

 #include<bits/stdc++.h>
 using namespace std;
 int main(){
     freopen("data.in","w",stdout);
     srand(time(NULL));
     printf("5\n");
     for(int i=;i<=;i++){
     printf("39999\n39999\n");
    for(int i=;i<=;i++){
         printf("1 %d %d\n",i,i%);
     }
     for(int i=;i<=;i++){
       printf("1 1 2 0\n");
     }
   printf("0 1\n");
    }
     return ;
 }

在自己电脑上测的话毕竟不太准，那么我们可以借助一个很好的平台——洛谷

我在洛谷创建了一个题目，数据用的是极端数据（就是用上面的代码生成的数据）

链接

（这里为了关照一下bitset，我把内存限制开大了，为了更清晰的比较，我把时间限制调到了10s，而且都没有开O2优化）

大家可以拿自己的代码试一下，看一下会不会T掉

这是我的测试结果

map

第1组数据是最极限的那一种，2到5组数据也会卡枚举的方法，但没那么严重，6到10是小数据

我们发现map的效率比较稳定，取决于n的大小，是一种不错的方法

枚举

枚举的话，卡枚举的前5组都超过了2秒，即使时间开到了10s，最极限的第一组也会T掉，但是随机数据还是很快的

bitset

biset初始化会占用大量时间，不划算，小数据也会跑到几百毫秒

而且内存开到336.82MB也不现实，所以还是用map吧

总结：如果数据随机的话我觉得差别不大，map每次查询是log(n)，不管数据如何都比较稳定，直接爆搜随机数据还可以，但极限数据或特别的构图可能会超时

biset的话内存是个短板