Xenon's Attack on the Gangs（树规）

题干

Input

Output

Example

Test 1:						Test 2:
3							5
1 2							1 2
2 3 						1 3
							1 4
							3 5

3							10

Tips

译成人话

给n个结点，n-1条无向边。即一棵树。我们需要给这n-1条边赋上0~ n-2不重复的值。mex(u,v)表示从结点u到结点v经过的边权值中没有出现的最小非负整数。计算下面等式的最大值：

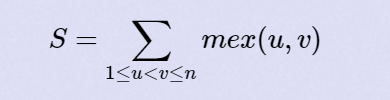
扯淡时间到：

看到题，头皮发麻，怎么想也想不出来，越是想越是觉得人是真的有极限的，于是，我不做人啦，老师！！

另外，我突然找到了一个很不错的视频题解？？？我大B站无所不有Σ(っ °Д °;)っ

咳~不玩梗了，关于这道题 ，我自己的确是没什么思路，所以，还是感谢郭军凯大佬和刘畅大佬的题解，给我这个小蒟蒻指了条明路 ：D

首先，我们来看下面这张图：



我们一眼就能看到u1u2这条权值为0的边把这一堆节点分成了左右两堆，那么，根据定义我们能知道，无论是左还是右，只要是同一堆中的节点相互到达，答案一定是0，因为边肯定不经过0嘛，而0又肯定是最小的权。而如果左右两堆中的节点互相到达，那么一定要经过u1u2边也就是0权边，所以它的答案最小是1（不确定，因为我们不知道剩下的边权是多少，但最小一定是1，因为自然数中除了0就是1最小，更多的2，3，4…也是以此类推）

那么下一步，我们肯定是要一个个赋边权，那么怎么赋呢？下一步我们要赋值边权1，能考虑的边有u1v1,u1v2,v1v3,u2v4,u2v5…太多了。那么，我们再看一张图：



如图，我把v1v3这条边赋值为1，那么u1到v1，u1到v2，答案显然都是1，因为路径没经过1这条边，只有v1到v3答案为2，因为经过了1权边。

那么，我把u1v1这条边赋为1呢？



我们会发现，u1到v1，v1到v3，现在都经过了边权为1的边，此时答案都变成了2，显然比原来更大了。据此，我们可以推断，边权1赋给与0权边相邻的边时，答案最大，即最优。当赋边权2，边权3…时也是同理。

那么现在的问题是，与0权边相邻的边有u1v1,u1v2,u2v4,u2v5，这么多，我们该选哪个呢？



我们定义如图数组，在添加边权1之前，对于所有节点，只要路径经过u1u2即0权边，那么答案一定是1，对总答案贡献为siz[u1]*siz[u2]；而路径不经过0权边的，跟一开始提到的一样答案都是0，对总答案没有贡献。所以此时在没加1权边时，除开u1u2外，总答案为 siz[u1]*siz[u2];



还是这张图，我们让它变得更一般化一点，u1u2表示为已确定权值的一条边，节点u1可表示为fa[v5][v1],节点u2表示为fa[v1][v5]。

我们的下一步加权选择有u1v1,u1v2,u2v4,u2v5,这里我只拿u1v1,u2v5两条边举例，别的边也是一样的道理，反正都会枚举到的。

如果我把下一个边权加在u1v1上，增大的答案就是1*siz[v1][v5]*siz[v5][v1]（我们默认是按自然数从小到大顺序加权，每次权值都差1，故系数是1），再加上原来的dis[v1][fa[v1][v5]]；

同理，把下一个边权加在u2v5上，增大的答案也是1*siz[v1][v5]*siz[v5][v1]，再加上原来的dis[v5][fa[v5][v1]]；

增大的答案都是一样的，所以我们最终比较的是dis[v1][fa[v1][v5]]和dis[v5][fa[v5][v1]]的大小，我们要取较大的那一个。

然后这题的思路就结束了，我们的步骤就是先预处理出siz[ ]和fa[ ][ ],再枚举i,j按公式找到dis[i][j]的最大值（这里要递归来找，因为我们不能保证枚举的顺序正好满足dis也是从小到大的顺序，中间会有空档，所以要递归）

最后的最后，开long long已经是常规操作了吧。

代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
const int maxn=3005;
int head[maxn],len=0,n;
int root;
ll dis[maxn][maxn],fa[maxn][maxn],siz[maxn][maxn];
//dis[i][j]表示把从i到j间的m条边赋值0~m-1能得到的最大值
//fa[i][j]表示以i为根时，j的父节点
//siz[i][j]表示以i为根时，j节点的子树大小
struct Edge{
    int next,to;
}edge[maxn<<1];
void Add(int u,int v){
    edge[++len].next=head[u];
    edge[len].to=v;
    head[u]=len;
}
void Init(int u,int pa){//预处理fa[i][j]和siz[i][j]
    siz[root][u]=1;//每节点的初始子树规模都是1，因为它自己就是一个节点

    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(v==pa) continue;
        fa[root][v]=u;//更新v的父节点
        Init(v,u);//向子树方向递归
        siz[root][u]+=siz[root][v];//更新子树规模:siz[父]+=siz[子]
    }
}
long long Update(int u,int v){
    if(u==v) return 0;//自己到自己肯定是0
    if(dis[u][v]) return dis[u][v];//记忆化，减少重复计算
    return (dis[u][v]=max(Update(u,fa[u][v]),Update(v,fa[v][u]))+siz[u][v]*siz[v][u]);//向下递归
}
int main(){
    cin>>n;
    int x,y;
    for(int i=1;i<n;i++){
        scanf("%d%d",&x,&y);
        Add(x,y),Add(y,x);
    }
    for(int i=1;i<=n;i++){
        root=i;
        Init(i,-1);
    }
    ll ans=0;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++){
        ans=max(Update(i,j),ans);//递归寻找答案的最大值
    }
    cout<<ans<<endl;
    return 0;
}