[Luogu P1006]传纸条 (网格DP)
题面
传送门:https://www.luogu.org/problemnew/show/P1006
Solution
挺显然但需要一定理解的网络(应该是那么叫吧)DP
首先有一个显然但重要的结论要发现:从左上走到右下再从右下走回左上=从左上走两次到右下
那么接下来可以考虑:
设f[i][j][k][l]为第一次走到了(i,j)第二次走到了(k,l) 在路径不交错为前提下的能取到的最大友好值
转移方程也挺好写的
考虑这种情况能从哪里转移过来就好(i,j)可以从(i-1,j)或(i,j-1)转移过来,(k,l)可以从(k-1,l)或(k-1,l-1)转移过来
排列组合一下,总共4种可能性,取个最大值再加上a[i][j]和a[k][l]就好
当然(i==k and j==l) 即两个点重合的情况直接continue,因为f 的意义是之前的不重合,当前的也不能重合
预处理整个f设为0就好
时间复杂度O(n^4) n=50,显然能过
接下来我们可以考虑一个优化
因为我们两次从左上到右下是一起走的
就有这么一个推论: i+j = k+l (画个图就好,挺好发现的)
既然这两个相等,也就意味着我们可以通过总和与i,k推算出j,l
然后我们的方程就可以优化成这样的:
f[i][j][k]的意思为:走了i步,第一次走到了第j行,第二次走到了第k行
它们的橫坐标分别为:i-j+2,i-k+2
转移同理
这样,时间复杂度就可以优化为O(n^3),相较之前的可以称为巨大的飞跃
然后就OjbK了
Code
//Luogu P1006 传纸条
//May,4th,2018
//网格DP
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{
long long x=0,f=1; char c=getchar();
while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
while(isdigit(c)){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int N=50+5;
int f[2*N][N][N],a[N][N],n,m;
int main()
{
m=read(),n=read();
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
a[i][j]=read(); int MAX=n+m;
for(int i=1;i<=MAX;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=m;k++)
{
int X1=i-j+2,Y1=j,X2=i-k+2,Y2=k;
if((X1==X2 and Y1==Y2)==false and X1>0 and X2>0 and X1<=n and X2<=n)
{
f[i][j][k]=max(f[i][j][k],f[i-1][j][k]);
f[i][j][k]=max(f[i][j][k],f[i-1][j-1][k]);
f[i][j][k]=max(f[i][j][k],f[i-1][j][k-1]);
f[i][j][k]=max(f[i][j][k],f[i-1][j-1][k-1]);
f[i][j][k]+=a[j][X1]+a[k][X2];
}
} printf("%d",max(f[m+n-3][m][m-1],f[m+n-3][m-1][m]));
return 0;
}
C++(正解)
后记
当时想为什么不会交叉的时候考虑了挺久的,这种类型的网格DP还是得多学习一个,我啊,太naive了
我太弱了
[Luogu P1006]传纸条 (网格DP)的更多相关文章
- P1006 传纸条[棋盘DP]
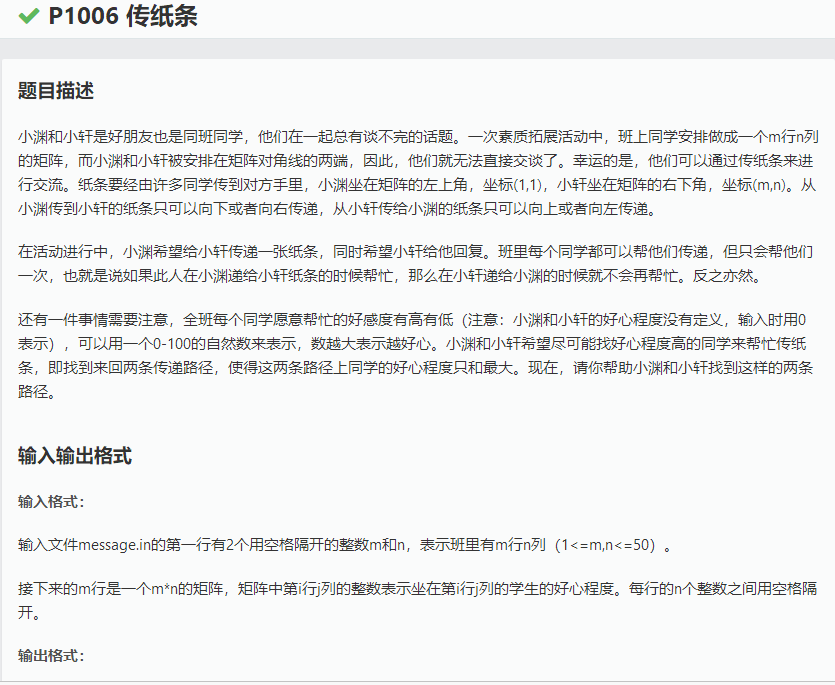
题目来源:洛谷 题目描述 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学安排做成一个m行n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接 ...
- 【暑假集训】HZOI2019 Luogu P1006 传纸条 二三四维解法
写三次丢失两次,我谔谔,以后再不在博客园先保存我就去死 题目内容 洛谷链接 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学被安排坐成一个\(m\)行.\(n\ ...
- 洛谷P1006 传纸条【dp】
题目:https://www.luogu.org/problemnew/show/P1006 题意: 给定一个m*n的矩阵,从(1,1)向下或向右走到(m,n)之后向上或向左走回(1,1),要求路径中 ...
- LuoGu P1006 传纸条
题目传送门 这题嘛...方格取数和这题一样一样的 只不过这题是从左上到右下再回去罢了(来回一趟和来两趟有区别么?没有,那么这题和上题用一样的转移和状态就行了 没什么好说的,说一下我的错误好了: 人家图 ...
- 棋盘DP三连——洛谷 P1004 方格取数 &&洛谷 P1006 传纸条 &&Codevs 2853 方格游戏
P1004 方格取数 题目描述 设有N $\times N$N×N的方格图(N $\le 9$)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字00.如下图所示(见样例): A ...
- P1006 传纸条(二维、三维dp)
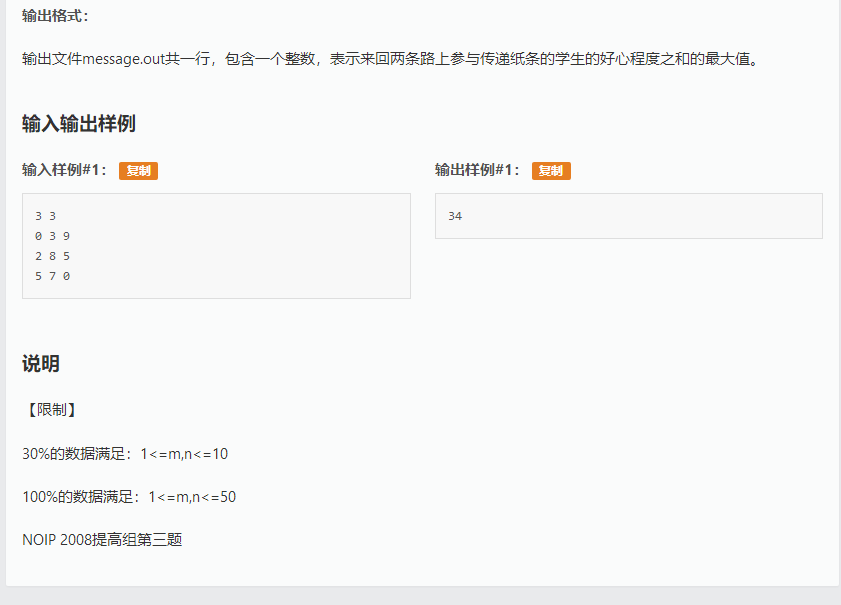
P1006 传纸条 输入输出样例 输入 #1 复制 3 3 0 3 9 2 8 5 5 7 0 输出 #1 复制 34 说明/提示 [限制] 对于 30% 的数据,1≤m,n≤10: 对于 100% ...
- Luogu 1006 传纸条 / NOIP 2008 传纸条(动态规划)
Luogu 1006 传纸条 / NOIP 2008 传纸条(动态规划) Description 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学安排做成一个m ...
- 【洛谷】【动态规划(多维)】P1006 传纸条
[题目描述:] 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学安排做成一个m行n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法直接交谈了.幸 ...
- 洛谷 P1006 传纸条 题解
P1006 传纸条 题目描述 小渊和小轩是好朋友也是同班同学,他们在一起总有谈不完的话题.一次素质拓展活动中,班上同学安排做成一个m行n列的矩阵,而小渊和小轩被安排在矩阵对角线的两端,因此,他们就无法 ...
随机推荐
- 对抗生成网络 Generative Adversarial Networks
1. Basic idea 基本任务:要得到一个generator,能够模拟想要的数据分布.(一个低维向量到一个高维向量的映射) discriminator就像是一个score function. 如 ...
- JS实现动态显示时间(最简单方法)
使用JS实现动态显示时间 最简单实现方法 直接在网页适当的位置中插入如下js代码,(id="datetime") 不可省略. <div id="datetime&q ...
- Python实现的数据结构与算法之链表详解
一.概述 链表(linked list)是一组数据项的集合,其中每个数据项都是一个节点的一部分,每个节点还包含指向下一个节点的链接.根据结构的不同,链表可以分为单向链表.单向循环链表.双向链表.双向循 ...
- python图像的绘制
转载:https://blog.csdn.net/haoji007/article/details/52063168 实际上前面我们就已经用到了图像的绘制,如: io.imshow(img) 这一行代 ...
- ATMEGA的SPI总线 - 第1部分
转自: 1. https://www.yiboard.com/thread-782-1-1.html 2.https://mansfield-devine.com/speculatrix/2018/0 ...
- JDBC Java 连接 MySQL 数据库
MySQL 版本:Server version: 5.7.17-log MySQL Community Server (GPL) 用于测试的 MySQL 数据库:game 查看数据库中的表 mysql ...
- P3118 [USACO15JAN]Moovie Mooving G
P3118 [USACO15JAN]Moovie Mooving G Link 题目描述 Bessie is out at the movies. Being mischievous as alway ...
- P4107 [HEOI2015]兔子与樱花 贪心
题目描述 传送门 分析 一道贪心题 首先我们可以证明最优的贡献一定是从下依次合并到上的 不会出现一个节点不能合并到父亲节点,却能合并到父亲节点的祖先节点的情况 我们设当前的节点为 \(u\),\(u\ ...
- ANNdotNET中的视觉神经网络设计器
ANNdotNET简介 是一个在.net平台上进行深度学习的开源项目.NET Framework和.NET Core).该项目位于http://github.com/bhrnjica/anndotne ...
- jquery购物车全选,取消全选,计算总金额
这是html代码 <div class="gwcxqbj"> <div class="gwcxd center"> <div cl ...
