C++图论算法——图的储存方式

使用二维数组邻接矩阵储存图

无向图：

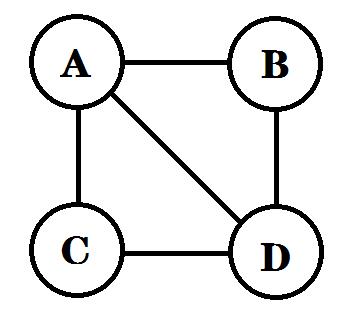图G

定义图G[101][101]，G[i][j]的值表示从结点v_i到v_j是否有边或弧，若有，取值为1或权值，若无，则取值为0或∞。以下是图G用邻接矩阵表示的列表：

 

结点	A	B	C	D
A	0	1	1	1
B	1	0	0	1
C	1	0	0	1
D	1	1	1	0

有向图：

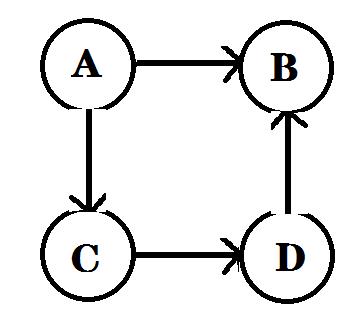图G（无权值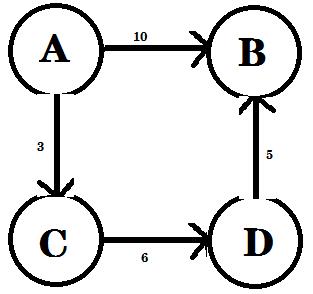）图G（有权值）

定义图G[101][101]，G[i][j]的值表示从结点v_i到v_j是否有边或弧，若有，取值为1或权值，若无，则取值为0或∞。以下是图G用邻接矩阵表示的列表：

结点	A	B	C	D
A	∞	1	1	∞
B	∞	∞	∞	∞
C	∞	∞	∞	1
D	∞	1	∞	∞

结点	A	B	C	D
A	∞	10	3	∞
B	∞	∞	∞	∞
C	∞	∞	∞	6
D	∞	5	∞	∞

#include <iostream>
#include <cstring>
using namespace std;

double G[101][101];
int main(){
    int u,v,t,n,m;                        // 结点u到结点v的节点值为t
    cin >> n;
    for (int i = 1;i <= n;i++){
        for (int j = 1;j <= n;j++){
            G[i][j] = 0x7fffffff;        // 初始化为无穷大
        }
    }
    // 或者使用memset(G,0x7fffffff,sizeof(G))来初始化
    /*
    若是int类型数组，则采用memset(G,0x7f,sizeof(G)))
    0x7fffffff表示无穷大,若是无向图，那么要写成memset(G,0,sizeof(G))
    也可以定义成memset(G,oxaf,sizeof(G)),全都定义成很小的数。
    */
    cin >> m;
    for (int i = 1;i <= m;i++){
        cin >> u >> v >> t;
        G[u][v] = t;G[v][u] = t;        // 邻接矩阵的值
    }
    // 输出
    for (int i = 1;i <= n;i++){
        for (int j = 1;j <= n;j++){
            cout << G[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

这是定义邻接矩阵的代码，大家可以根据需要查看注释修改代码。