P1337 [JSOI2004]平衡点（模拟退火）题解

题意：

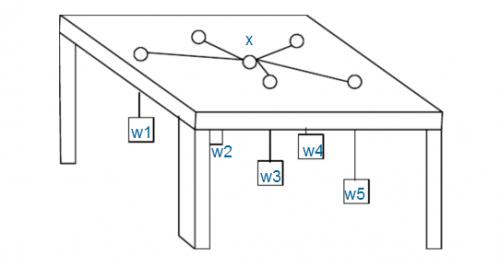
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

思路：

用模拟退火去搞。他问最后稳定在哪，即是问在哪个点能量最小。那么就用模拟退火去找最小能量点。

在模拟退火的时候，可以增大\(t0\)，或者增大\(t\)，或者增加模拟退火次数来增加精确度。还有一种优化就是，每次模拟退火找到一个最优解，那么再花几千次去这个点附近小范围围找找看有没有最优解，这样比直接多次退火效率高（听别人说的）。

参考：

浅谈玄学算法——模拟退火

洛谷P1337 【[JSOI2004]平衡点 / 吊打XXX】（模拟退火）

代码：

#include<set>
#include<map>
#include<cmath>
#include<queue>
#include<bitset>
#include<string>
#include<cstdio>
#include<vector>
#include<cstring>
#include <iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1000 + 10;
const ll INF = 1e18;
const ll MOD = 1e9 + 7;

const double t0 = 0.995;
const double eps = 1e-14;
double ansx, ansy, ans = INF;
struct Point{
    double x, y, w;
}p[maxn];
int n;
double solve(double x, double y){
    double ret = 0;
    for(int i = 1; i <= n; i++){
        ret += sqrt((p[i].x - x) * (p[i].x - x) + (p[i].y - y) * (p[i].y - y)) * p[i].w;
    }
    return ret;
}
void sa(){
    double t = 2000;
    double X = ansx, Y = ansy;
    while(t > eps){
        double x = X + (rand() * 2 - RAND_MAX) * t;
        double y = Y + (rand() * 2 - RAND_MAX) * t;
        double now = solve(x, y);
        double del = now - ans;
        if(del < 0){    //接受
            X = x, Y = y;
            ansx = x, ansy = y;
            ans = now;
        }
        else if(exp(-del / t) * RAND_MAX > rand()){
            //一定概率接受
            X = x, Y = y;
        }
        t *= t0;
    }
}
char s[maxn];
int main(){
    srand(131313131);
    srand(rand());
    scanf("%d", &n);
    double x = 0, y = 0;
    for(int i = 1; i <= n; i++){
        scanf("%lf%lf%lf", &p[i].x, &p[i].y, &p[i].w);
        x += p[i].x, y += p[i].y;
    }
    ansx = x / n, ansy = y / n; //平均数
    for(int i = 1; i <= 10; i++) sa();
    printf("%.3f %.3f\n", ansx, ansy);
    return 0;
}