KL变换

covariance 指两个变量的相关性：cov(x, y) =E(x y) - E(x) E(y)

cov(x, y) < 0 负相关

cov(x, y) = 0 无关

cov(x, y) > 0 正相关

covariance matrix : Ki,j = cov(xi, xj)

以下例子中，x为输入，y为输出

K-L变换被广泛应用在图像压缩领域中，是一个线性变换(W是正交矩阵)

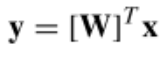
K-L变换的目标：通过KLT去除原数据之间的相关性，即解相关(decorrelatation)，设y的协方差矩阵为

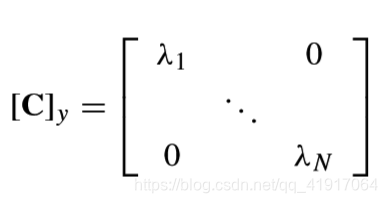
假设x的每个列向量均值为0，由线性变换的性质，y的每个列向量均值也为0，则

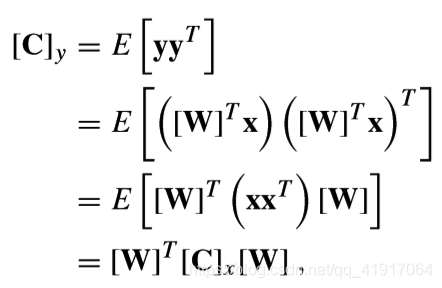
因为W是正交矩阵，上式可写为

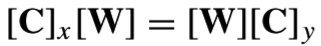
设为W的列向量，则

所以分别是的特征值和特征向量，即

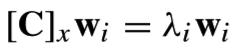
这样我们可以通过求的特征向量得到变换矩阵W

参考：https://blog.csdn.net/qq_41917064/article/details/103820786

所以可以通过求eigenvalue和eigenvector：I 是identic matrix

det( [C]x - λ I) = 0；

（[C]x - λ I）wi = 0