[COCI 2023/2024 #1] Mostovi 题解
前言
题目链接:洛谷。
题目分析
首先可以确定的是需要枚举断边,所以我们希望两次枚举之间能有些关联。不难想到类树形 DP 的套路,建 DFS 树,只不过这题除了讨论和父亲之间的边,还要考虑返租边。以下钦定以 \(1\) 为树根。
树边
先从简单的树边开始考虑。考虑不经过 \(u\) 和 \(u\) 的父亲 \(v\),对答案是否产生贡献。为方便实现,记录的是操作后整张图依旧联通的边数。
分为两种情况讨论。
- \(v\) 为树根。
- \(v\) 仅有 \(u\) 一个儿子。操作后整张图依旧联通。
- \(v\) 还有另一个儿子 \(yzh\)。整张图联通当且仅当 \(u\) 是叶子结点,不然 \(u\) 的子孙和 \(yzh\) 就断开了。
- \(v\) 还有多个儿子。无论怎样,由于不能经过 \(v\),剩下来的孩子都互不连通。
- \(v\) 为内部节点。
- 最好的情况,\(v\) 的所有子树都能向上连到 \(v\) 的祖先,\(u\) 的所有子树同样能连到 \(v\) 的祖先,操作后整张图依旧连通。
- \(u\) 是叶子结点,并且 \(v\) 的其他子树都能连到 \(v\) 的祖先,操作后整张图依旧连通。
- 其他情况操作后图均不连通。
可以通过下图辅助理解。
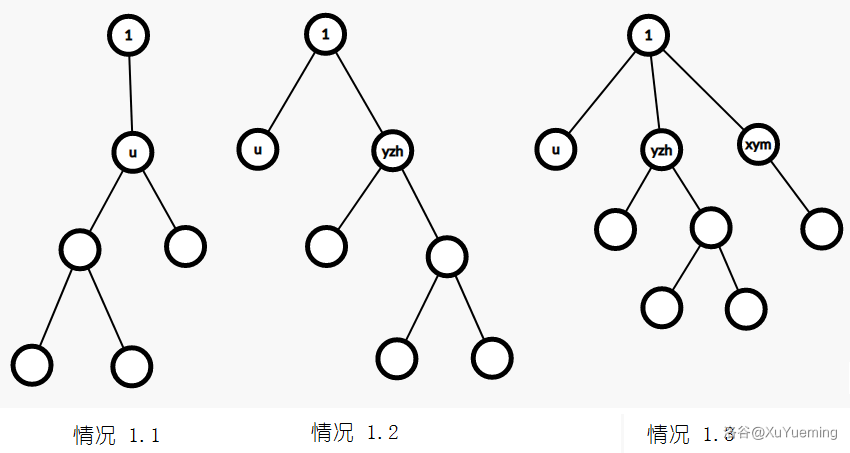
具体实现时,按照上述方法模拟即可。具体如下:
- 用一次 dfs 记录 \(1\) 的儿子数量和 \(u\) 儿子数量,再用一次 dfs 统计答案即可。
- 用一次 dfs 求出以 \(u\) 为根的子树通过一条返租边能到达的最深结点,和次深结点。由于返租边的另一边只能是祖先结点,所以可以用深度来代替返租边另一边的结点。再用另一次 dfs 按照如下顺序求解。
- \(u\) 有一个结点不能连到 \(u\) 的祖先,那么不管如何,删去 \(u\) 这个点一定会导致图不连通。
- \(u\) 的某一个子树只有一条返租边连向 \(u\) 的祖先 \(xym\),那么如果存在 \(u \rightarrow xym\) 这条边,删去后图不连通,可以用一个数据结构维护不能删去的点(实际记录深度即可)。
- 考虑 \(u \rightarrow v\) 这条树边,如果 \(v \neq xym\) 并且 \(v\) 的子树中没有不能连向 \(v\) 的祖先的子树,或者仅有一个并且其为身为叶子结点的 \(u\),删去后图依旧联通。
非树边
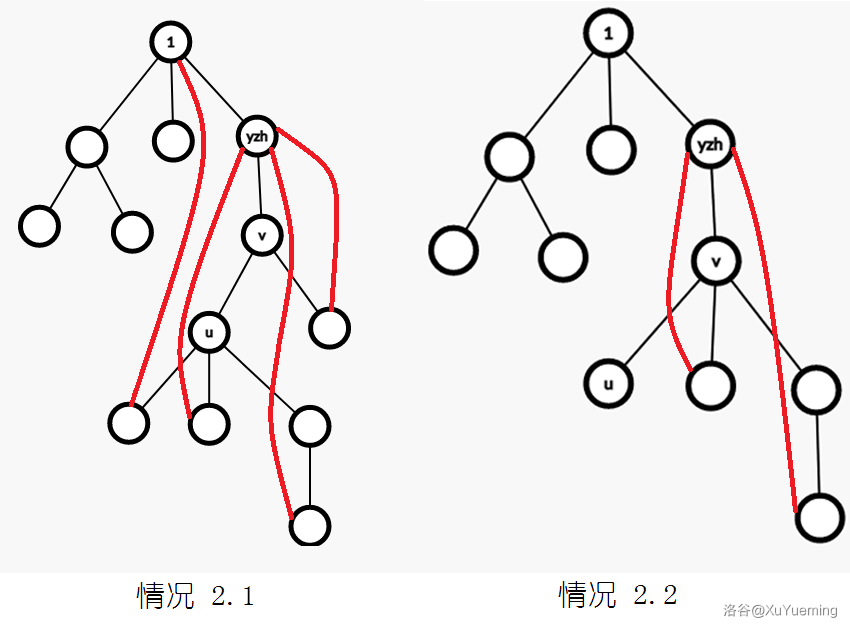
考虑完树边,再来看看相对复杂的非树边 \(u \rightarrow yzh\),易知 \(yzh\) 一定是 \(u\) 的祖先。
经过我们观察,删去非树边比删去树边多出了 \(u \rightarrow \cdots \rightarrow yzh\) 这一条链上的部分,即 \(yzh\) 的子树减去 \(u\) 的子树,如下图蓝色部分。
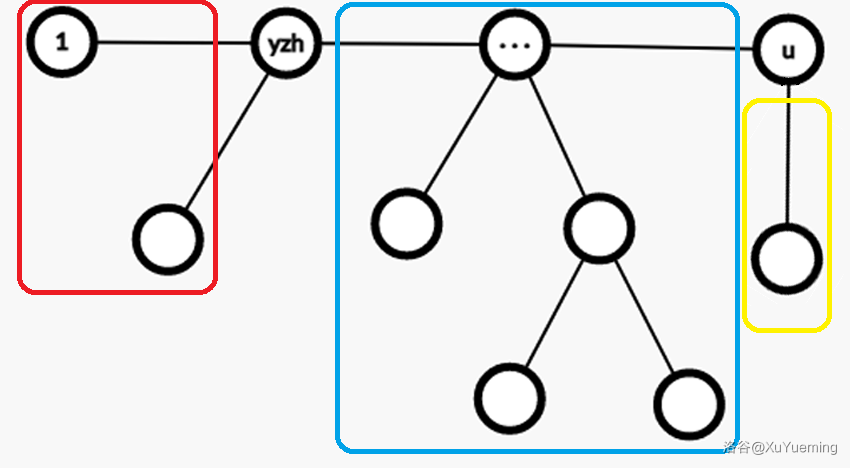
所以我们考虑图的连通性的时候就要算上它们,其他和以上讨论类似。
- \(yzh\) 是树根,按照以上特判即可。
- 红色部分不连通,删去一定不连通。
- \(u\) 有一棵子树既不能连到红色部分,又不能连到蓝色部分,删去一定不连通。
- \(u\) 为叶子结点,或者所有子树能和红色或蓝色其中一个部分连通,当且仅当红色和蓝色部分连通,删去后连通。
- 有一棵子树既和红色部分连通又和蓝色部分连通,删去图依旧联通。
- 其他情况删去一定不连通。
很抽象是吧,这道题目考验我们强大的逻辑推理能力,做到情况不漏,实现细心。所以来讲讲具体实现。
- 按照树边特判即可。
- 记录 \(yzh\) 有多少棵子树不与 \(yzh\) 祖先连通,如果大于一个,删去不连通。
- 这种情况相当于有一棵子树不能练到 \(u\) 的祖先结点,这个同上解决。也一样记录特殊情况,即 \(u\) 的某一个子树只有一条返租边连向 \(u\) 的祖先 \(xym\),那么不能删掉 \(xym\) 这个点。
- 我们想知道蓝色部分能不能连到红色部分,发现可以用倍增解决出蓝色部分能连出的最浅深度。这个倍增不能包含 \(u\) 子树的信息。
- 相当于 \(yzh\) 处在 \(u\) 连出的某两条边之间,那么记录 \(u\) 子树中能连出的最浅深度,这个要比 \(yzh\) 浅,然后记录连到 \(u\) 祖先最深的深度,这个要比 \(yzh\) 深。前者第一次 dfs 可以预处理出,后者发现需要将子树里的返租边,但是反不到 \(u\) 的返租边删除,即只保留另一端深度小于 \(u\) 的返租边。这个可以用 dfs 序加线段树或者左偏树,但是最方便的做法当然是愉快地启发式合并啦。
代码(已略去快读快写)
讲了这么多,实际代码需要格外的小心,注意细节。令 \(n\) 和 \(m\) 同阶,那么整体时间复杂度是 \(\Theta(n \log ^ 2 n)\) 或者 \(\Theta(n \log n)\) 的。
左偏树
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <algorithm>
#include <vector>
#include <set>
const int inf = 0x3f3f3f3f;
const int N = 100010;
const int M = 300010;
const int lgN = __lg(N) + 2;
struct Graph{
struct node{
int to, nxt;
} edge[M << 1];
int eid, head[N];
inline void add(int u, int v){
edge[++eid] = {v, head[u]};
head[u] = eid;
}
inline node & operator [] (const int x){
return edge[x];
}
} xym;
struct node{
int fi, se;
node (int fi = inf, int se = inf): fi(fi), se(se) {}
inline node operator + (const int val) const {
node res(fi, se);
if (val < fi) res.se = res.fi, res.fi = val;
else if (fi < val && val < se) res.se = val;
return res;
}
inline node operator + (const node & o) const {
return *this + o.fi + o.se;
}
inline node & operator += (const node & o) {
return *this = *this + o;
}
};
int n, m, ans;
int dpt[N], yzh[N][lgN];
int L[N], R[N], timer;
vector<int> son[N];
node f[N][lgN], pos[N], s[N];
int sum[N], who[N];
void dfs(int now){
L[now] = ++timer, dpt[now] = dpt[yzh[now][0]] + 1;
vector<node> l, r; int cnt = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (to == yzh[now][0]) continue;
if (dpt[to]) pos[now] += dpt[to];
else {
son[now].push_back(to), yzh[to][0] = now, ++cnt;
dfs(to), s[now] += s[to], l.push_back(s[to]), r.push_back(s[to]);
if (s[to].fi >= dpt[now]) ++sum[now], who[now] = to;
}
}
for (int i = 1; i < cnt; ++i) l[i] += l[i - 1];
for (int i = cnt - 2; i >= 0; --i) r[i] += r[i + 1];
for (int i = 0; i < cnt; ++i){
int to = son[now][i];
if (i > 0) f[to][0] += l[i - 1];
if (i + 1 < cnt) f[to][0] += r[i + 1];
f[to][0] += pos[now];
}
R[now] = timer, s[now] += pos[now];
}
int root[N], tot;
int deleted[M], dtop;
int lson[M], rson[M], val[M];
int dist[M];
int newNode(int val){
int res = dtop ? deleted[dtop--] : ++tot;
lson[res] = rson[res] = dist[res] = 0;
::val[res] = val;
return res;
}
int combine(int x, int y){
if (!x || !y) return x | y;
if (val[x] < val[y]) swap(x, y);
rson[x] = combine(rson[x], y);
if (dist[rson[x]] > dist[lson[x]]) swap(lson[x], rson[x]);
return dist[x] = dist[rson[x]] + 1, x;
}
void redfs(int now){
set<int> not_ok;
set<pair<int, int> > stt;
bool flag = false;
for (const auto& to: son[now]){
redfs(to);
while (root[to] && val[root[to]] >= dpt[now]){
deleted[++dtop] = root[to];
root[to] = combine(lson[root[to]], rson[root[to]]);
}
if (root[to] && val[root[to]] != s[to].fi)
stt.insert({val[root[to]], s[to].fi});
root[now] = combine(root[now], root[to]);
if (s[to].fi >= dpt[now]) flag = true;
else if (s[to].se >= dpt[now]) not_ok.insert(s[to].fi);
}
vector<pair<int, int> > l(stt.begin(), stt.end()); stt.clear();
int tot = l.size();
for (int i = tot - 2; i >= 0; --i)
l[i].second = min(l[i].second, l[i + 1].second);
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (dpt[to] > dpt[now]) continue;
root[now] = combine(root[now], newNode(dpt[to]));
if (to == 1){
if (sum[to] != 1){
if (to == yzh[now][0] && son[now].size() == 0u && sum[to] == 2) ++ans;
} else {
if (to == yzh[now][0] && son[now].size() != 1u) continue;
if (to != yzh[now][0] && (flag || not_ok.count(1))) continue;
++ans;
}
continue;
}
if (flag) continue;
if (to != yzh[now][0]){
node sum; int u = now;
for (int k = lgN - 1; k >= 0; --k)
if (yzh[u][k] && dpt[yzh[u][k]] > dpt[to])
sum += f[u][k], u = yzh[u][k];
if (sum.fi >= dpt[to]){
vector<pair<int, int> >::iterator it =
upper_bound(l.begin(), l.end(), pair<int, int>{dpt[to], inf});
if (it == l.end() || it -> second >= dpt[to]) continue;
}
}
if (sum[to] > 1) continue;
if (sum[to] != 0 && (L[now] < L[who[to]] || R[who[to]] < L[now])) continue;
if (not_ok.count(dpt[to])) continue;
++ans;
}
}
signed main(){
read(n, m);
for (int i = 1, u, v; i <= m; ++i) read(u, v), xym.add(u, v), xym.add(v, u);
dfs(1);
for (int k = 1; k < lgN; ++k)
for (int i = 1; i <= n; ++i){
yzh[i][k] = yzh[yzh[i][k - 1]][k - 1];
f[i][k] = f[i][k - 1] + f[yzh[i][k - 1]][k - 1];
}
redfs(1), write(m - ans);
return 0;
}
启发式合并
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <algorithm>
#include <vector>
#include <set>
const int inf = 0x3f3f3f3f;
const int N = 100010;
const int M = 300010;
const int lgN = __lg(N) + 2;
struct Graph{
struct node{
int to, nxt;
} edge[M << 1];
int eid, head[N];
inline void add(int u, int v){
edge[++eid] = {v, head[u]};
head[u] = eid;
}
inline node & operator [] (const int x){
return edge[x];
}
} xym;
struct node{
int fi, se;
node (int fi = inf, int se = inf): fi(fi), se(se) {}
inline node operator + (const int val) const {
node res(fi, se);
if (val < fi) res.se = res.fi, res.fi = val;
else if (fi < val && val < se) res.se = val;
return res;
}
inline node operator + (const node & o) const {
return *this + o.fi + o.se;
}
inline node & operator += (const node & o) {
return *this = *this + o;
}
};
int n, m, ans;
int dpt[N], yzh[N][lgN];
int L[N], R[N], timer;
vector<int> son[N];
node f[N][lgN], pos[N], s[N];
int sum[N], who[N];
void dfs(int now){
L[now] = ++timer, dpt[now] = dpt[yzh[now][0]] + 1;
vector<node> l, r; int cnt = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (to == yzh[now][0]) continue;
if (dpt[to]) pos[now] += dpt[to];
else {
son[now].push_back(to), yzh[to][0] = now, ++cnt;
dfs(to), s[now] += s[to], l.push_back(s[to]), r.push_back(s[to]);
if (s[to].fi >= dpt[now]) ++sum[now], who[now] = to;
}
}
for (int i = 1; i < cnt; ++i) l[i] += l[i - 1];
for (int i = cnt - 2; i >= 0; --i) r[i] += r[i + 1];
for (int i = 0; i < cnt; ++i){
int to = son[now][i];
if (i > 0) f[to][0] += l[i - 1];
if (i + 1 < cnt) f[to][0] += r[i + 1];
f[to][0] += pos[now];
}
R[now] = timer, s[now] += pos[now];
}
set<int> st[N];
inline void merge(set<int> &a, set<int>& b){
if (a.size() < b.size()) a.swap(b);
for (const auto& x: b) a.insert(x);
b.clear();
}
void redfs(int now){
set<int> not_ok;
set<pair<int, int> > stt;
bool flag = false;
for (const auto& to: son[now]){
redfs(to);
while (!st[to].empty() && *st[to].rbegin() >= dpt[now])
st[to].erase(prev(st[to].end()));
if (st[to].size() > 1u) stt.insert({*st[to].rbegin(), *st[to].begin()});
merge(st[now], st[to]);
if (s[to].fi >= dpt[now]) flag = true;
else if (s[to].se >= dpt[now]) not_ok.insert(s[to].fi);
}
vector<pair<int, int> > l(stt.begin(), stt.end()); stt.clear();
int tot = l.size();
for (int i = tot - 2; i >= 0; --i)
l[i].second = min(l[i].second, l[i + 1].second);
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (dpt[to] > dpt[now]) continue;
st[now].insert(dpt[to]);
if (to == 1){
if (sum[to] != 1){
if (to == yzh[now][0] && son[now].size() == 0u && sum[to] == 2) ++ans;
} else {
if (to == yzh[now][0] && son[now].size() != 1u) continue;
if (to != yzh[now][0] && (flag || not_ok.count(1))) continue;
++ans;
}
continue;
}
if (flag) continue;
if (to != yzh[now][0]){
node sum; int u = now;
for (int k = lgN - 1; k >= 0; --k)
if (yzh[u][k] && dpt[yzh[u][k]] > dpt[to])
sum += f[u][k], u = yzh[u][k];
if (sum.fi >= dpt[to]){
vector<pair<int, int> >::iterator it =
upper_bound(l.begin(), l.end(), pair<int, int>{dpt[to], inf});
if (it == l.end() || it -> second >= dpt[to]) continue;
}
}
if (sum[to] > 1) continue;
if (sum[to] != 0 && (L[now] < L[who[to]] || R[who[to]] < L[now])) continue;
if (not_ok.count(dpt[to])) continue;
++ans;
}
}
signed main(){
read(n, m);
for (int i = 1, u, v; i <= m; ++i) read(u, v), xym.add(u, v), xym.add(v, u);
dfs(1);
for (int k = 1; k < lgN; ++k)
for (int i = 1; i <= n; ++i){
yzh[i][k] = yzh[yzh[i][k - 1]][k - 1];
f[i][k] = f[i][k - 1] + f[yzh[i][k - 1]][k - 1];
}
redfs(1), write(m - ans);
return 0;
}
dfs 序加线段树
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <unordered_set>
#include <algorithm>
#include <vector>
#include <set>
const int inf = 0x3f3f3f3f;
const int N = 100010;
const int M = 300010;
const int lgN = __lg(N) + 2;
struct Graph{
struct node{
int to, nxt;
} edge[M << 1];
int eid, head[N];
inline void add(const int &u, const int &v){
edge[++eid] = {v, head[u]};
head[u] = eid;
}
inline node & operator [] (const int x){
return edge[x];
}
} xym;
struct node{
int fi, se;
inline node (int fi = inf, int se = inf): fi(fi), se(se) {}
inline void merge(const node & o){
this -> merge(o.fi);
this -> merge(o.se);
}
inline void merge(const int val){
if (val < fi) se = fi, fi = val;
else if (fi < val && val < se) se = val;
}
};
int n, m, ans;
int real_lgN;
int dpt[N], yzh[N][lgN];
int L[N], R[N], timer;
vector<int> son[N], rev[N];
node f[N][lgN], pos[N], s[N];
int sum[N], who[N];
void dfs(int now){
L[now] = ++timer, dpt[now] = dpt[yzh[now][0]] + 1;
vector<node> l, r; int cnt = 0;
for (register int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (to == yzh[now][0]) continue;
if (dpt[to]){
pos[now].merge(dpt[to]);
if (dpt[to] <= dpt[now]) rev[now].emplace_back(to);
} else {
son[now].emplace_back(to), yzh[to][0] = now;
rev[to].emplace_back(now);
dfs(to), s[now].merge(s[to]), l.emplace_back(s[to]);
if (s[to].fi >= dpt[now]) ++sum[now], who[now] = to;
}
}
r = l, cnt = son[now].size();
for (register int i = cnt - 2; i >= 0; --i) r[i].merge(r[i + 1]);
for (register int i = 0; i < cnt; ++i){
register int to = son[now][i];
(i > 0) && (f[to][0].merge(l[i - 1]), l[i].merge(l[i - 1]), yzh_i_love_you);
(i + 1 < cnt) && (f[to][0].merge(r[i + 1]), yzh_i_love_you);
f[to][0].merge(pos[now]);
}
R[now] = timer, s[now].merge(pos[now]);
}
int iL[N], iR[N], itimer;
int val[M];
void build(int now){
iL[now] = itimer + 1;
for (const auto& to: rev[now]) val[++itimer] = dpt[to];
for (const auto& to: son[now]) build(to);
iR[now] = itimer;
}
struct Segment_Tree{
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct Info{
int maxx, maxpos;
int minn, minpos;
inline Info operator + (const Info& o) const {
if (maxx == -inf) return o;
if (o.maxx == -inf) return *this;
return {maxx > o.maxx ? maxx : o.maxx, maxx > o.maxx ? maxpos : o.maxpos,
minn < o.minn ? minn : o.minn, minn < o.minn ? minpos : o.minpos};
}
};
struct node{
int l, r;
Info info;
} tree[M << 2];
inline void pushup(int idx){
tree[idx].info = tree[lson].info + tree[rson].info;
}
void build(int idx, int l, int r){
tree[idx] = {l, r, {-inf, -1, inf, -1}};
if (l == r) return tree[idx].info = {val[l], l, val[l], l}, void();
int mid = (l + r) >> 1;
build(lson, l, mid), build(rson, mid + 1, r);
pushup(idx);
}
Info query(int idx, int l, int r){
if (tree[idx].l > r || tree[idx].r < l) return {-inf, -1, inf, -1};
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].info;
return query(lson, l, r) + query(rson, l, r);
}
void erase(int idx, int p){
if (tree[idx].l > p || tree[idx].r < p) return;
if (tree[idx].l == tree[idx].r) return tree[idx].info = {-inf, -1, inf, -1}, void();
erase(lson, p), erase(rson, p), pushup(idx);
}
#undef lson
#undef rson
} tree;
void redfs(int now){
if (iL[now] > iR[now]) return;
unordered_set<int> not_ok;
vector<pair<int, int> > l;
bool flag = false;
for (const auto& to: son[now]){
redfs(to);
while (iL[to] <= iR[to]){
Segment_Tree::Info res = tree.query(1, iL[to], iR[to]);
if (res.minn == inf || res.maxx == -inf) break;
if (res.maxx < dpt[now]) break;
tree.erase(1, res.maxpos);
}
if (iL[to] <= iR[to]){
Segment_Tree::Info res = tree.query(1, iL[to], iR[to]);
if (res.minn != inf && res.maxx != -inf && res.minn != res.maxx)
l.emplace_back(res.maxx, res.minn);
}
if (s[to].fi >= dpt[now]) flag = true;
else if (s[to].se >= dpt[now]) not_ok.insert(s[to].fi);
}
sort(l.begin(), l.end());
int tot = l.size();
for (register int i = tot - 2; i >= 0; --i)
l[i].second = Fast::min(l[i].second, l[i + 1].second);
for (const auto& to: rev[now]){
if (to == 1){
if (sum[to] != 1){
if (to == yzh[now][0] && son[now].size() == 0u && sum[to] == 2) ++ans;
} else {
if (to == yzh[now][0] && son[now].size() != 1u) continue;
if (to != yzh[now][0] && (flag || not_ok.count(1))) continue;
++ans;
}
continue;
}
if (flag) continue;
if (to != yzh[now][0]){
node sum; register int u = now;
for (register int k = real_lgN - 1; k >= 0; --k)
if (yzh[u][k] && dpt[yzh[u][k]] > dpt[to])
sum.merge(f[u][k]), u = yzh[u][k];
if (sum.fi >= dpt[to]){
vector<pair<int, int> >::iterator it =
upper_bound(l.begin(), l.end(), pair<int, int>{dpt[to], inf});
if (it == l.end() || it -> second >= dpt[to]) continue;
}
}
if (sum[to] > 1 || not_ok.count(dpt[to])) continue;
if (sum[to] != 0 && (L[now] < L[who[to]] || R[who[to]] < L[now])) continue;
++ans;
}
}
signed main(){
read(n, m), real_lgN = __lg(n) + 2;
for (int i = 1, u, v; i <= m; ++i) read(u, v), xym.add(u, v), xym.add(v, u);
dfs(1);
for (register int k = 1; k < real_lgN; ++k)
for (register int i = 1; i <= n; ++i){
yzh[i][k] = yzh[yzh[i][k - 1]][k - 1];
f[i][k] = f[i][k - 1];
if (yzh[i][k - 1]) f[i][k].merge(f[yzh[i][k - 1]][k - 1]);
}
build(1), tree.build(1, 1, itimer), redfs(1), write(m - ans);
return 0;
}
线段树合并
补题降智以为 \(\Theta(n \log n)\) 的线段树合并是 \(\Theta(\log n)\) 的,总的时间复杂度是 \(\Theta(n ^ 2 \log n)\) 的,喜提 TLE。但是还是放出来吧,写都写了。
UPDATE on 2024.4.7
好吧,写题解更降智。 维护一个权值线段树,然后向上合并。你干嘛要删除啊,每次查询 \([1, dpt[now])\) 里的最大值就行了,这样就不会超时。
AC code
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <unordered_set>
#include <algorithm>
#include <vector>
#include <set>
const int inf = 0x3f3f3f3f;
const int N = 100010;
const int M = 300010;
const int lgN = __lg(N) + 2;
struct Graph{
struct node{
int to, nxt;
} edge[M << 1];
int eid, head[N];
inline void add(const int &u, const int &v){
edge[++eid] = {v, head[u]};
head[u] = eid;
}
inline node & operator [] (const int x){
return edge[x];
}
} xym;
struct node{
int fi, se;
inline node (int fi = inf, int se = inf): fi(fi), se(se) {}
inline void merge(const node & o){
this -> merge(o.fi);
this -> merge(o.se);
}
inline void merge(const int val){
if (val < fi) se = fi, fi = val;
else if (fi < val && val < se) se = val;
}
};
int n, m, ans;
int real_lgN;
int dpt[N], yzh[N][lgN];
int L[N], R[N], timer;
vector<int> son[N], rev[N];
node f[N][lgN], pos[N], s[N];
int sum[N], who[N];
void dfs(int now){
L[now] = ++timer, dpt[now] = dpt[yzh[now][0]] + 1;
vector<node> l, r; int cnt = 0;
for (register int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (to == yzh[now][0]) continue;
if (dpt[to]){
pos[now].merge(dpt[to]);
if (dpt[to] <= dpt[now]) rev[now].emplace_back(to);
} else {
son[now].emplace_back(to), yzh[to][0] = now;
rev[to].emplace_back(now);
dfs(to), s[now].merge(s[to]), l.emplace_back(s[to]);
if (s[to].fi >= dpt[now]) ++sum[now], who[now] = to;
}
}
r = l, cnt = son[now].size();
for (register int i = cnt - 2; i >= 0; --i) r[i].merge(r[i + 1]);
for (register int i = 0; i < cnt; ++i){
register int to = son[now][i];
(i > 0) && (f[to][0].merge(l[i - 1]), l[i].merge(l[i - 1]), yzh_i_love_you);
(i + 1 < cnt) && (f[to][0].merge(r[i + 1]), yzh_i_love_you);
f[to][0].merge(pos[now]);
}
R[now] = timer, s[now].merge(pos[now]);
}
int root[N];
struct Combinable_Segment_Tree{
struct node{
int lson, rson;
int maxx;
} tree[N << 5];
int tot;
int deleted[N << 4], dtop;
int NewNode(){
int now = dtop ? deleted[dtop--] : ++tot;
tree[now] = {0, 0, -inf};
return now;
}
inline node & operator [] (const int x){
return tree[x];
}
inline void pushup(int idx){
if (tree[idx].lson && tree[idx].rson){
tree[idx].maxx = Fast::max(tree[tree[idx].lson].maxx, tree[tree[idx].rson].maxx);
} else if (tree[idx].lson){
tree[idx].maxx = tree[tree[idx].lson].maxx;
} else if (tree[idx].rson){
tree[idx].maxx = tree[tree[idx].rson].maxx;
} else {
tree[idx].maxx = -inf;
}
}
void insert(int &idx, int trl, int trr, int p){
if (trl > p || trr < p) return;
if (!idx) idx = NewNode();
if (trl == trr) return tree[idx].maxx = p, void();
int mid = (trl + trr) >> 1;
insert(tree[idx].lson, trl, mid, p);
insert(tree[idx].rson, mid + 1, trr, p);
pushup(idx);
}
int combine(int idx, int oidx, int trl, int trr){
if (!idx || !oidx) return idx | oidx;
if (trl == trr) return tree[idx].maxx = tree[oidx].maxx, idx;
int mid = (trl + trr) >> 1;
tree[idx].lson = combine(tree[idx].lson, tree[oidx].lson, trl, mid);
tree[idx].rson = combine(tree[idx].rson, tree[oidx].rson, mid + 1, trr);
return pushup(idx), idx;
}
int query(int idx, int trl, int trr, int l, int r){
if (!idx || trl > r || trr < l) return -inf;
if (l <= trl && trr <= r) return tree[idx].maxx;
int mid = (trl + trr) >> 1;
return max(query(tree[idx].lson, trl, mid, l, r), query(tree[idx].rson, mid + 1, trr, l, r));
}
} tree;
void redfs(int now){
unordered_set<int> not_ok;
vector<pair<int, int> > l;
bool flag = false;
for (const auto& to: son[now]){
redfs(to);
if (root[to] && dpt[now] != 1){
int maxx = tree.query(root[to], 1, n, 1, dpt[now] - 1);
if (maxx != -inf && s[to].fi != maxx && s[to].fi != -inf)
l.emplace_back(maxx, s[to].fi);
}
root[now] = tree.combine(root[now], root[to], 1, n);
if (s[to].fi >= dpt[now]) flag = true;
else if (s[to].se >= dpt[now]) not_ok.insert(s[to].fi);
}
sort(l.begin(), l.end());
int tot = l.size();
for (register int i = tot - 2; i >= 0; --i)
l[i].second = Fast::min(l[i].second, l[i + 1].second);
for (const auto& to: rev[now]){
tree.insert(root[now], 1, n, dpt[to]);
if (to == 1){
if (sum[to] != 1){
if (to == yzh[now][0] && son[now].size() == 0u && sum[to] == 2) ++ans;
} else {
if (to == yzh[now][0] && son[now].size() != 1u) continue;
if (to != yzh[now][0] && (flag || not_ok.count(1))) continue;
++ans;
}
continue;
}
if (flag) continue;
if (to != yzh[now][0]){
node sum; register int u = now;
for (register int k = real_lgN - 1; k >= 0; --k)
if (yzh[u][k] && dpt[yzh[u][k]] > dpt[to])
sum.merge(f[u][k]), u = yzh[u][k];
if (sum.fi >= dpt[to]){
vector<pair<int, int> >::iterator it =
upper_bound(l.begin(), l.end(), pair<int, int>{dpt[to], inf});
if (it == l.end() || it -> second >= dpt[to]) continue;
}
}
if (sum[to] > 1 || not_ok.count(dpt[to])) continue;
if (sum[to] != 0 && (L[now] < L[who[to]] || R[who[to]] < L[now])) continue;
++ans;
}
}
signed main(){
read(n, m), real_lgN = __lg(n) + 2;
for (int i = 1, u, v; i <= m; ++i) read(u, v), xym.add(u, v), xym.add(v, u);
dfs(1);
for (register int k = 1; k < real_lgN; ++k)
for (register int i = 1; i <= n; ++i){
yzh[i][k] = yzh[yzh[i][k - 1]][k - 1];
f[i][k] = f[i][k - 1];
if (yzh[i][k - 1]) f[i][k].merge(f[yzh[i][k - 1]][k - 1]);
}
redfs(1), write(m - ans);
return 0;
}
TLE code
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <unordered_set>
#include <algorithm>
#include <vector>
#include <set>
const int inf = 0x3f3f3f3f;
const int N = 100010;
const int M = 300010;
const int lgN = __lg(N) + 2;
struct Graph{
struct node{
int to, nxt;
} edge[M << 1];
int eid, head[N];
inline void add(const int &u, const int &v){
edge[++eid] = {v, head[u]};
head[u] = eid;
}
inline node & operator [] (const int x){
return edge[x];
}
} xym;
struct node{
int fi, se;
inline node (int fi = inf, int se = inf): fi(fi), se(se) {}
inline void merge(const node & o){
this -> merge(o.fi);
this -> merge(o.se);
}
inline void merge(const int val){
if (val < fi) se = fi, fi = val;
else if (fi < val && val < se) se = val;
}
};
int n, m, ans;
int real_lgN;
int dpt[N], yzh[N][lgN];
int L[N], R[N], timer;
vector<int> son[N], rev[N];
node f[N][lgN], pos[N], s[N];
int sum[N], who[N];
void dfs(int now){
L[now] = ++timer, dpt[now] = dpt[yzh[now][0]] + 1;
vector<node> l, r; int cnt = 0;
for (register int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to;
if (to == yzh[now][0]) continue;
if (dpt[to]){
pos[now].merge(dpt[to]);
if (dpt[to] <= dpt[now]) rev[now].emplace_back(to);
} else {
son[now].emplace_back(to), yzh[to][0] = now;
rev[to].emplace_back(now);
dfs(to), s[now].merge(s[to]), l.emplace_back(s[to]);
if (s[to].fi >= dpt[now]) ++sum[now], who[now] = to;
}
}
r = l, cnt = son[now].size();
for (register int i = cnt - 2; i >= 0; --i) r[i].merge(r[i + 1]);
for (register int i = 0; i < cnt; ++i){
register int to = son[now][i];
(i > 0) && (f[to][0].merge(l[i - 1]), l[i].merge(l[i - 1]), yzh_i_love_you);
(i + 1 < cnt) && (f[to][0].merge(r[i + 1]), yzh_i_love_you);
f[to][0].merge(pos[now]);
}
R[now] = timer, s[now].merge(pos[now]);
}
int root[N];
struct Combinable_Segment_Tree{
struct node{
int lson, rson;
int minn, maxx;
} tree[N << 4];
int tot;
inline node & operator [] (const int x){
return tree[x];
}
inline void pushup(int idx){
if (tree[idx].lson && tree[idx].rson){
tree[idx].minn = Fast::min(tree[tree[idx].lson].minn, tree[tree[idx].rson].minn);
tree[idx].maxx = Fast::max(tree[tree[idx].lson].maxx, tree[tree[idx].rson].maxx);
} else if (tree[idx].lson){
tree[idx].minn = tree[tree[idx].lson].minn;
tree[idx].maxx = tree[tree[idx].lson].maxx;
} else if (tree[idx].rson){
tree[idx].minn = tree[tree[idx].rson].minn;
tree[idx].maxx = tree[tree[idx].rson].maxx;
} else {
tree[idx].minn = inf, tree[idx].maxx = -inf;
}
}
void insert(int &idx, int trl, int trr, int p){
if (trl > p || trr < p) return;
if (!idx) tree[idx = ++tot] = {0, 0, inf, -inf};
if (trl == trr) return tree[idx].minn = tree[idx].maxx = p, void();
int mid = (trl + trr) >> 1;
insert(tree[idx].lson, trl, mid, p);
insert(tree[idx].rson, mid + 1, trr, p);
pushup(idx);
}
void erase(int &idx, int trl, int trr, int p){
if (trl > p || trr < p) return;
if (!idx) tree[idx = ++tot] = {0, 0, inf, -inf};
if (trl == trr) return tree[idx].minn = inf, tree[idx].maxx = -inf, void();
int mid = (trl + trr) >> 1;
erase(tree[idx].lson, trl, mid, p);
erase(tree[idx].rson, mid + 1, trr, p);
pushup(idx);
}
int combine(int idx, int oidx, int trl, int trr){
if (!idx || !oidx) return idx | oidx;
if (trl == trr) return tree[idx].maxx = tree[oidx].maxx, tree[idx].minn = tree[oidx].minn, idx;
int mid = (trl + trr) >> 1;
tree[idx].lson = combine(tree[idx].lson, tree[oidx].lson, trl, mid);
tree[idx].rson = combine(tree[idx].rson, tree[oidx].rson, mid + 1, trr);
return pushup(idx), idx;
}
} tree;
void redfs(int now){
unordered_set<int> not_ok;
vector<pair<int, int> > l;
bool flag = false;
for (const auto& to: son[now]){
redfs(to);
while (root[to]){
int minn = tree[root[to]].minn, maxx = tree[root[to]].maxx;
if (minn == inf || maxx == -inf) break;
if (maxx < dpt[now]) break;
tree.erase(root[to], 1, n, maxx);
}
if (root[to]){
int minn = tree[root[to]].minn, maxx = tree[root[to]].maxx;
if (minn != inf && maxx != -inf && minn != maxx)
l.emplace_back(maxx, minn);
}
root[now] = tree.combine(root[now], root[to], 1, n);
if (s[to].fi >= dpt[now]) flag = true;
else if (s[to].se >= dpt[now]) not_ok.insert(s[to].fi);
}
sort(l.begin(), l.end());
int tot = l.size();
for (register int i = tot - 2; i >= 0; --i)
l[i].second = Fast::min(l[i].second, l[i + 1].second);
for (const auto& to: rev[now]){
tree.insert(root[now], 1, n, dpt[to]);
if (to == 1){
if (sum[to] != 1){
if (to == yzh[now][0] && son[now].size() == 0u && sum[to] == 2) ++ans;
} else {
if (to == yzh[now][0] && son[now].size() != 1u) continue;
if (to != yzh[now][0] && (flag || not_ok.count(1))) continue;
++ans;
}
continue;
}
if (flag) continue;
if (to != yzh[now][0]){
node sum; register int u = now;
for (register int k = real_lgN - 1; k >= 0; --k)
if (yzh[u][k] && dpt[yzh[u][k]] > dpt[to])
sum.merge(f[u][k]), u = yzh[u][k];
if (sum.fi >= dpt[to]){
vector<pair<int, int> >::iterator it =
upper_bound(l.begin(), l.end(), pair<int, int>{dpt[to], inf});
if (it == l.end() || it -> second >= dpt[to]) continue;
}
}
if (sum[to] > 1 || not_ok.count(dpt[to])) continue;
if (sum[to] != 0 && (L[now] < L[who[to]] || R[who[to]] < L[now])) continue;
++ans;
}
}
signed main(){
read(n, m), real_lgN = __lg(n) + 2;
for (int i = 1, u, v; i <= m; ++i) read(u, v), xym.add(u, v), xym.add(v, u);
dfs(1);
for (register int k = 1; k < real_lgN; ++k)
for (register int i = 1; i <= n; ++i){
yzh[i][k] = yzh[yzh[i][k - 1]][k - 1];
f[i][k] = f[i][k - 1];
if (yzh[i][k - 1]) f[i][k].merge(f[yzh[i][k - 1]][k - 1]);
}
redfs(1), write(m - ans);
return 0;
}
[COCI 2023/2024 #1] Mostovi 题解的更多相关文章
- 百度之星初赛A 今夕何夕
今夕何夕 今天是2017年8月6日,农历闰六月十五. 小度独自凭栏,望着一轮圆月,发出了"今夕何夕,见此良人"的寂寞感慨. 为了排遣郁结,它决定思考一个数学问题:接下来最近的哪一年 ...
- Bzoj索引
1001 : http://ideone.com/4omPYJ1002 : http://ideone.com/BZr9KF1003 : http://ideone.com/48NJNh1004 : ...
- Hsql中In没有1000的限制
SELECT * FROM user , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ...
- HDU 6112 今夕何夕
今夕何夕 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
- 日期求星期(java)-蓝桥杯
日期求星期问题(java)-蓝桥杯 1:基姆拉尔森计算公式(计算星期) 公式: int week = (d+2*m+3*(m+1)/5+y+y/4-y/100+y/400)%7; 此处y,m,d指代年 ...
- 解决Nginx重启时提示nginx: [emerg] bind() to 0.0.0.0:80错误
Nginx是一款轻量级的Web服务器,特点是占有内存少,并发能力强,因而使用比较广泛,蜗牛今天在一个VPS上重启Nginx时提示“nginx: [emerg] bind() to 0.0.0.0:80 ...
- 2017"百度之星"程序设计大赛 - 初赛(A) 01,05,06
小C的倍数问题 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Problem ...
- HDU 2021 发工资咯:)(最水贪心)
传送门: http://acm.hdu.edu.cn/showproblem.php?pid=2021 发工资咯:) Time Limit: 2000/1000 MS (Java/Others) ...
- 百度之星2017初赛A-1005-今夕何夕
今夕何夕 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
- [SinGuLaRiTy] 2017 百度之星程序设计大赛 初赛A
[SinGuLaRiTy-1036] Copyright (c) SinGuLaRiTy 2017. All Rights Reserved. 小C的倍数问题 Time Limit: 2000/100 ...
随机推荐
- idea如何快速找到项目中待处理的TODO注释
idea如何快速找到项目中待处理的TODO注释 idea菜单栏 View -> Tool Windows,可以打开TODO窗口
- Thread的join方法demo
Thread的join方法demo /** * 关于join官方的解释是 Waits for this thread to die. 也就是等待一个线程结束. */ public class Thre ...
- svn服务端安装和使用
首先去官网下载安装包 点我下载 下载完了以后选择安装路径然后一直next就可以了 安装完了以后在开始菜单里面找到svn 打开 如何使用? 这里是创建代码管理的存储库 点击 repositories ...
- python 注册nacos 进行接口规范定义
背景: 一般场景 python服务经常作为java下游的 算法服务或者 数据处理服务 但是使用http 去调用比较不灵活,通过注册到nacos上进行微服务调用才是比较爽的 1.定义feginapi的接 ...
- 工具类——EventManager
EventManager using UnityEngine; using System.Collections; using System.Collections.Generic; using Un ...
- 【golang】json数据中复杂key的处理
例1 type Transport struct { Time string Id int } func main() { //将struct的切片包装成json格式 var st []Transpo ...
- Python_9 py文件导入和路径处理
一.查缺补漏 Python中两个值交换可以直接交换如:a,b=b,a 冒泡就是从小到大排序,因为越到后越大 自动导包也适用于自己创建的模块 关于正斜杠和反斜杠https://www.cnblogs.c ...
- 全志T113-i+玄铁HiFi4开发板硬件说明书(2)
前 言 本文档主要介绍开发板硬件接口资源以及设计注意事项等内容,测试板卡为全志T113-i+玄铁HiFi4开发板,由于篇幅问题,本篇文章共分为上下两集,点击账户可查看更多内容详情,开发问题欢迎留言,感 ...
- P6626 题解
有一个很暴力的解法,就是以询问点为根 DFS. 考虑优化,我们考虑优化换根. 当根节点从父亲移动到它的某个孩子时,孩子的子树内所有点深度减 \(1\) 其余点深度加 \(1\). 同理,当根节点从某个 ...
- SpringBoot学习备忘
在 mapper.xml 中的 like 的写法 db1.name like "%"#{name}"%" 参考mybatis mapper.xml中like的写 ...
