LeetCode 3093. 最长公共后缀查询 （二分法）

LeetCode 3093. 最长公共后缀查询

1 题目描述

给你两个字符串数组 wordsContainer 和 wordsQuery 。

对于每个 wordsQuery[i] ，你需要从 wordsContainer 中找到一个与 wordsQuery[i] 有 最长公共后缀 的字符串。如果 wordsContainer 中有两个或者更多字符串有最长公共后缀，那么答案为长度 最短 的。如果有超过两个字符串有 相同 最短长度，那么答案为它们在 wordsContainer 中出现 更早 的一个。

请你返回一个整数数组 ans ，其中 ans[i]是 wordsContainer中与 wordsQuery[i] 有 最长公共后缀 字符串的下标。

示例 1：

输入：wordsContainer = ["abcd","bcd","xbcd"], wordsQuery = ["cd","bcd","xyz"]

输出：[1,1,1]

解释：

我们分别来看每一个 wordsQuery[i] ：

• 对于 wordsQuery[0] = "cd" ，wordsContainer 中有最长公共后缀 "cd" 的字符串下标分别为 0 ，1 和 2 。这些字符串中，答案是下标为 1 的字符串，因为它的长度为 3 ，是最短的字符串。
• 对于 wordsQuery[1] = "bcd" ，wordsContainer 中有最长公共后缀 "bcd" 的字符串下标分别为 0 ，1 和 2 。这些字符串中，答案是下标为 1 的字符串，因为它的长度为 3 ，是最短的字符串。
• 对于 wordsQuery[2] = "xyz" ，wordsContainer 中没有字符串跟它有公共后缀，所以最长公共后缀为 "" ，下标为 0 ，1 和 2 的字符串都得到这一公共后缀。这些字符串中， 答案是下标为 1 的字符串，因为它的长度为 3 ，是最短的字符串。

示例 2：

输入：wordsContainer = ["abcdefgh","poiuygh","ghghgh"], wordsQuery = ["gh","acbfgh","acbfegh"]

输出：[2,0,2]

解释：

我们分别来看每一个 wordsQuery[i] ：

• 对于 wordsQuery[0] = "gh" ，wordsContainer 中有最长公共后缀 "gh" 的字符串下标分别为 0 ，1 和 2 。这些字符串中，答案是下标为 2 的字符串，因为它的长度为 6 ，是最短的字符串。
• 对于 wordsQuery[1] = "acbfgh" ，只有下标为 0 的字符串有最长公共后缀 "fgh" 。所以尽管下标为 2 的字符串是最短的字符串，但答案是 0 。
• 对于 wordsQuery[2] = "acbfegh" ，wordsContainer 中有最长公共后缀 "gh" 的字符串下标分别为 0 ，1 和 2 。这些字符串中，答案是下标为 2 的字符串，因为它的长度为 6 ，是最短的字符串。

提示：

• 1 <= wordsContainer.length, wordsQuery.length <= 104
• 1 <= wordsContainer[i].length <= 5 * 103
• 1 <= wordsQuery[i].length <= 5 * 103
• wordsContainer[i] 只包含小写英文字母。
• wordsQuery[i] 只包含小写英文字母。
• wordsContainer[i].length 的和至多为 5 * 105 。
• wordsQuery[i].length 的和至多为 5 * 105 。

2 解题思路

这题最容易想到的方法应该就是字典树了，当然如果只是这样的话我也没有必要写这篇题解。

这里要介绍的方法是通过二分搜索，在使用几乎最少的额外空间下完成这道题。

2.1 翻转字符串

首先，我们需要将这个问题从后缀匹配转换为前缀匹配问题，也就是先把所有的字符串都进行一次翻转，在此过程中用map记录他们的下标。

后面要用到二分搜索，因此还需要进行一次排序，转换为有序数组。

unordered_map<string, int> index{};

int num = 0;
for (auto &words : wordsContainer)
{
    // 翻转字符串
    reverse(words.begin(), words.end());
    // 相同的字符串仅记录最早的下标
    if (!index.count(words))
    {
        index[words] = num;
    }
    num++;
}

sort(wordsContainer.begin(), wordsContainer.end());

2.2 二分搜索迭代

接下来我们就需要思考，该如何利用二分搜索来找到答案。

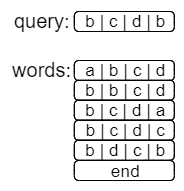
举个栗子，我们需要在words中寻找query对应的最大前缀。

如果我们直接以query为目标，在words中进行二分搜索，其结果肯定是不正确的。

换个角度思考，我们要找到是最长的前缀，那我们大可以不以query为目标，而是先用二分搜索，把所有b开头的字符串给找到。

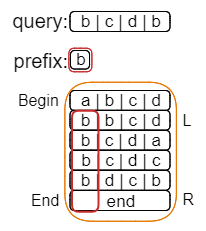
操作过程就如上图所示，其中橙色方框为查找的范围，红色方框则是搜索的结果，二者都是左闭右开区间。

其中搜索上界可以使用lower_bound，下界则是使用upper_bound。

可以看出，我们已经找到了开头为b的字符串，其范围是[1, 5)，所以我们就可以将查找的范围更新为[1, 5)。

而接下来的事情，想必你也能猜到了，那就是在此基础上继续查找第二个字符为c的字符串。

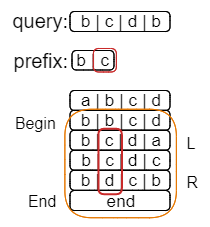
搜索范围从[1, 5)缩小到了[2, 4)，接着继续查找第三个字符为d的字符串。

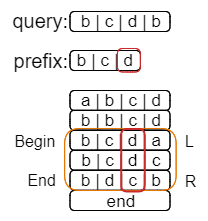
这次的结果还是[2, 4)，最后再查找第四个字符为b的字符串。

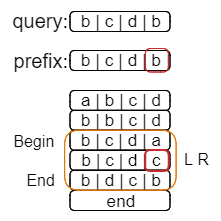
有意思的事情发生了，搜索的结果[4, 4)是一个空区间，这说明已经没有能够继续匹配的字符串。这就意味着上一个搜索的结果（也就是[2, 4)）就已经是能够找到的最长公共前缀字符串的区间了。

具体的代码如下：

auto begin = wordsContainer.begin();
auto end = wordsContainer.end();

for (string prefix{}; query.size(); query.pop_back())
{
    prefix.push_back(query.back());

    compare cmp(prefix.size() - 1);
    auto nBegin = lower_bound(begin, end, prefix, cmp);
    auto nEnd = upper_bound(begin, end, prefix, cmp);

    // nBegin == nEnd表示已经达到最大前缀匹配
    // 直接退出循环，在目前的[begin, end)范围中寻找最合适的结果
    if (nBegin == nEnd)
    {
        break;
    }

    begin = nBegin;
    end = nEnd;
}

2.3 遍历区间

最后，我们就可以根据题目的要求，在最终的区间内找出长度最短且出现最早的字符串的下标，作为本次查询的结果。

int minSize = INT32_MAX;
int minIndex = INT32_MAX;
while (begin != end)
{
    string &s = *begin++;
    if (s.size() < minSize ||
        s.size() == minSize && index[s] < minIndex)
    {
        minSize = s.size();
        minIndex = index[s];
    }
}
ans.push_back(minIndex);

2.4 比较函数

其实在二分搜索的那一节还有些问题没有解决，比如我们要如何实现搜索呢？

我们使用lower_bound和upper_bound函数定位的上下界时，比较的并不是传入的字符串，而是比较其中特定位置的字符，并且这个位置会随需求变化。这里就可以通过定义仿函数，来将每次比较所需要的下标信息传入其中。

class compare
{
public:
    compare(int index) : index(index) {}
    int index;
    bool operator()(const string &s1, const string &s2)
    {
        return /*返回比较的结果*/;
    }
};

先别急着在函数中返回s1[index] < s2[index]的结果，让我们接着分析一下具体情况。

首先，我们需要明确的是，比较函数中传入的两个参数，一个是待匹配的字符串words，另一个是当前前缀prefix。

从之前的搜索过程可以看出index = prefix.size() - 1，所以prefix绝对不会出现访问越界的情况，但words就不一定了。

当index小于s1.size()和s2.size()时，我们可以直接返回s1[index] < s2[index]

但是当words.size() <= index时，我们就需要分两种情况来判断。

1. s1 = words：s1[index]没有字符，视为最小值，因此s1[index] < s2[index] == true
2. s2 = words：s2[index]没有字符，视为最小值，因此s1[index] < s2[index] == false

我们将上述三种情况整理一下，用以下代码表示：

bool operator()(const string &s1, const string &s2)
{
    // if(s1.size() <= index) return true;
    // if(s2.size() <= index) return false;
    // return s1[index] < s2[index];

    return s1.size() <= index ||
            s2.size() > index && s1[index] < s2[index];
}

3 答案代码

最终代码如下：

class compare
{
public:
    compare(int index) : index(index) {}
    int index;
    bool operator()(const string &s1, const string &s2)
    {
        // if(s1.size() <= index) return true;
        // if(s2.size() <= index) return false;
        // return s1[index] < s2[index];

        return s1.size() <= index ||
               s2.size() > index && s1[index] < s2[index];
    }
};

vector<int> stringIndices(vector<string> &wordsContainer,
                          vector<string> &wordsQuery)
{
    vector<int> ans{};
    unordered_map<string, int> index{};

    int num = 0;
    for (auto &words : wordsContainer)
    {
        reverse(words.begin(), words.end());
        // 相同的字符串仅记录最早的下标
        if (!index.count(words))
        {
            index[words] = num;
        }
        num++;
    }
    sort(wordsContainer.begin(), wordsContainer.end());

    for (auto &query : wordsQuery)
    {
        auto begin = wordsContainer.begin();
        auto end = wordsContainer.end();

        for (string prefix{}; query.size(); query.pop_back())
        {
            prefix.push_back(query.back());

            compare cmp(prefix.size() - 1);
            auto nBegin = lower_bound(begin, end, prefix, cmp);
            auto nEnd = upper_bound(begin, end, prefix, cmp);

            // nBegin == nEnd表示已经达到最大前缀匹配
            // 直接退出循环，在目前的[begin, end)范围中寻找最合适的结果
            if (nBegin == nEnd)
            {
                break;
            }

            begin = nBegin;
            end = nEnd;
        }

        int minSize = INT32_MAX;
        int minIndex = INT32_MAX;
        while (begin != end)
        {
            string &s = *begin++;
            if (s.size() < minSize ||
                s.size() == minSize && index[s] < minIndex)
            {
                minSize = s.size();
                minIndex = index[s];
            }
        }
        ans.push_back(minIndex);
    }

    return ans;
}

---

本文发布于2024年3月27日

最后编辑于2024年3月27日