题解 ZOJ3203 Light Bulb

也就是loj上的#10016灯泡了...

---

先上原图：

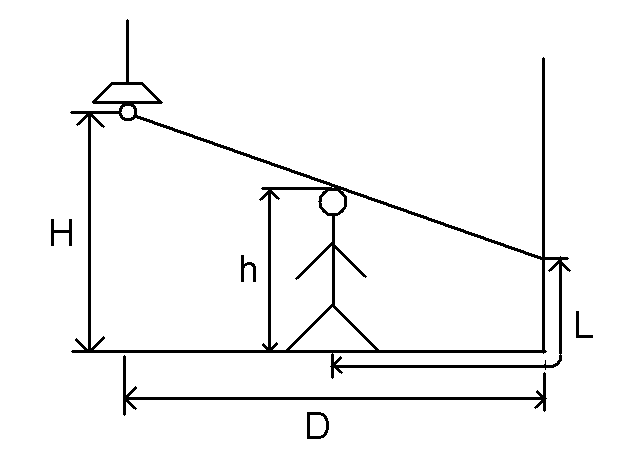
因为长度肯定是个开口向下的二次函数，所以先是确定用三分来找位置，然后想办法求出当前阴影长度

看到这条斜线，就想到了一次函数，所以就建了一个系，没想到还真解出来了。

---

首先设灯泡位置为(H,0)，再设它与人头之间连接的线段所在直线为y=kx+b

所以b=H(在灯泡处入x=0代可以解出来)，k=(h-b)/x=(h-H)/x(这个不用解释吧)

所以这条直线(也就是光线)与地面相交于y=0时

即x1=-b/k。

因为b,k已知，所以肯定求得出来

然后判断是否大于D

如果小于D，直接返回x1-x

如果大于D，那么在墙上的一截就是当x=D时，y的值，即y=k*D+b

这样就可以了

代码如下：

#include<cstdio>

double b,h,d,l,r;

inline double max(double a,double b){
    return a>b?a:b;
}    

inline double f(double x){
    double k=(h-b)/x;//求k
    double x1=-b/k;//求x1if(x1<=d)return x1-x;//判断
    return d-x+k*d+b;
}

int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%lf%lf%lf",&b,&h,&d);//干脆把b当H输入
        l=,r=d;
        while(l+1e-<r){//我这样写midl与midr只是图方便，不是有什么特殊的方法
            double midl=(l+r)/;
            double midr=(midl+r)/;
            if(f(midl)<=f(midr))l=midl;
            else r=midr;
        }
        printf("%.3lf\n",f(l));
    }
    return ;
}

完结撒花！！！✿✿ヽ(°▽°)ノ✿