Codeforces Round #337 (Div. 2) 610C Harmony Analysis(脑洞)

C. Harmony Analysis

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The semester is already ending, so Danil made an effort and decided to visit a lesson on harmony analysis to know how does the professor look like, at least. Danil was very bored on this lesson until the teacher gave the group a simple task: find 4 vectors
in 4-dimensional space, such that every coordinate of every vector is 1 or  - 1 and
any two vectors are orthogonal. Just as a reminder, two vectors in n-dimensional space are considered to be orthogonal if and only
if their scalar product is equal to zero, that is:

.

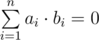
Danil quickly managed to come up with the solution for this problem and the teacher noticed that the problem can be solved in a more general case for 2k vectors
in 2k-dimensinoal
space. When Danil came home, he quickly came up with the solution for this problem. Can you cope with it?

Input

The only line of the input contains a single integer k (0 ≤ k ≤ 9).

Output

Print 2k lines
consisting of 2k characters
each. The j-th character of the i-th
line must be equal to ' * ' if the j-th
coordinate of the i-th vector is equal to  - 1,
and must be equal to ' + ' if it's equal to  + 1.
It's guaranteed that the answer always exists.

If there are many correct answers, print any.

Sample test(s)

input

2

output

++**
+*+*
++++
+**+

Note

Consider all scalar products in example:

• Vectors 1 and 2: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( + 1) + ( - 1)·( - 1) = 0
• Vectors 1 and 3: ( + 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 1 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( - 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 3: ( + 1)·( + 1) + ( - 1)·( + 1) + ( + 1)·( + 1) + ( - 1)·( + 1) = 0
• Vectors 2 and 4: ( + 1)·( + 1) + ( - 1)·( - 1) + ( + 1)·( - 1) + ( - 1)·( + 1) = 0
• Vectors 3 and 4: ( + 1)·( + 1) + ( + 1)·( - 1) + ( + 1)·( - 1) + ( + 1)·( + 1) = 0

题目链接:点击打开链接

在2^k维空间中构造2^k个相互垂直的向量.

观察给出的数据, 无限脑洞...

AC代码:

#include "iostream"
#include "cstdio"
#include "cstring"
#include "algorithm"
#include "queue"
#include "stack"
#include "cmath"
#include "utility"
#include "map"
#include "set"
#include "vector"
#include "list"
#include "string"
#include "cstdlib"
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
int n;
int main(int argc, char const *argv[])
{
	scanf("%d", &n);
	n = 1 << n;
	for(int i = 0; i < n; ++i) {
		for(int j = 0; j < n; ++j)
			printf("%c", __builtin_parity(i & j) ? '*' : '+');
		printf("\n");
	}
	return 0;
}

列举四个位运算函数:

• int __builtin_ffs (unsigned int x)
  
  返回x的最后一位1的是从后向前第几位，比方7368（1110011001000）返回4。
• int __builtin_clz (unsigned int x)
  
  返回前导的0的个数。

• int __builtin_ctz (unsigned int x)
  
  返回后面的0个个数，和__builtin_clz相对。

• int __builtin_popcount (unsigned int x)
  
  返回二进制表示中1的个数。

• int __builtin_parity (unsigned int x)
  
  返回x的奇偶校验位，也就是x的1的个数模2的结果。
• 摘自:点击打开链接