【Dijkstra+邻接表求次短路】POJ Sightseeing 3463

Language:
Default

Sightseeing

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 7766		Accepted: 2766

Description

Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights
alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.

Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients
a choice from many different routes. As hotels have been booked in advance, the starting city Sand the final city F, though, are fixed. Two routes from S to F are
considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.

There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F.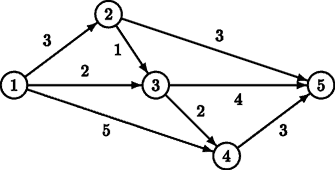
It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the
minimal routes. This enhances the impression of a personal holiday.

For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1
→ 3 → 4 → 5, of length 7.

Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction
on the route length.

Input

The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

• One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and
  the number of roads in the road map.

• M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and
  1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.

  The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different
  roads from a city A to a city B.

• One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F:
  the starting city and the final city of the route.

  There will be at least one route from S to F.

Output

For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10⁹ = 1,000,000,000.

Sample Input

2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1

Sample Output

3
2

Hint

The first test case above corresponds to the picture in the problem description.

Source

BAPC 2006 Qualification

题意：

旅行团从S地出发到达T地。为了省油要求尽量走最短路径或比最短路径长1单位距离的路径。求满足条件的路径条数

解题思路：

相信最短路非常easy求出来的，主要是次短路怎样求出？？？

我们能够先求出从S到T的次短路的距离。然后推断这个距离与最短距离是否相差为一？所以我们的任务就变成了求解次短路和最短路的问题。

（s。u，v）代表从s——v的最短路，u是中间一个必经点。

我们先看看最短路和次短路的比較：

①（s，u，v）最短路=到达前一个点u的最短路+（u。v）的最短路。

而最短路求解有两种情况：

①（s。u。v）次短路=到达前一个点u的次短路+（u。v）的最短路。

②（s，u，v）次短路=到达前一个点u的最短路+（u，v）的次短路。

所以根据次短路的求解条件。能够在求解最短路的时候求解次短路。

我们用：d[ v ][ 0 ]代表最短路，d[ v ] [ 1 ]代表次短路。

（一）假设从s—u的最短路加上（u，v）权值的距离小于原来的d[ v ][ 0 ] ，我们就可把次短路d[ v ][ 1 ] 的值更新为d[ v ][ 0 ]。就该题而言，此时能够把次短路的条数也更新为这个点的最短路的条数；把当前最短路d[ v ][ 0 ]的值更新成最小的，和原来最短路的松弛操作是一样的。

（二）假设从s—u的最短路加上（u。v）权值的距离大于原来的d[ v ][ 0 ]，这就说明这条路路径就可能是一条次短路，那我们须要推断这条路的值dist。和原来的次短路的值d[ v ][1]进行比較！

①假设它比原来的次短路要大，直接跳过。

②假设它比原来的次短路要小，那么我们就须要更新最短路的长度。

③假设与原来的次短路相等。说明我们的次短路有还有一种（这里并不一定是仅仅有1种）方法能够到达终点v。这里要加的种类是：原来到v点的次短路的条数+到u点的次短路（或者最短路。（u。v）并不知道是不是一定是最短路，假设是次短路，那么此时加的就是到u的最短路）的条数。

次短路的情况已经分析出来，最短路的情况是比較easy得出了的。和Dijkstra操作正常的松弛操作就能够了。只是本题让求路径条数。所以要在松弛操作出现相等情况时进行相加操作。这一点比較简单，不在分析，具体看代码。

  AC代码：

#include <stdio.h>
#include <math.h>
#include <vector>
#include <queue>
#include <string>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define INF 0x3f3f3f3f

using namespace std;

const int MAXN = 10010;
const int MAXM = 100010;

struct Edge
{
    int from;
    int to;
    int w;
    int next;
}edge[MAXN];

int tot;
int head[MAXM];

void addEdge(int u,int v,int w)
{
    edge[tot].from=u;
    edge[tot].to=v;
    edge[tot].w=w;
    edge[tot].next=head[u];
    head[u]=tot++;
}

int d[MAXM][2];//记录最短路、次短路距离。

int c[MAXN][2];//记录最短路、次短路路径条数。
int vis[MAXN][2];//记录最短路、次短路时该点是否被訪问过。
int N,M;

void Dijkstra(int s)
{
    int flag;
    int k;
    for(int i=1;i<=N;i++){
        c[i][0]=c[i][1]=0;
        d[i][0]=d[i][1]=INF;
        vis[i][0]=vis[i][1]=0;
    }
    d[s][0]=0;
    c[s][0]=1;
    int min_dist=INF;
    while(true){
        int v=-1;
        for(int i=1;i<=N;i++){ //我们并不能确定取出的最小值的就一定是最短路的点
            for(int j=0;j<2;j++){//所以要遍历次短和最短的点。
                if(!vis[i][j]&&(v==-1||d[i][j]<d[v][k])){
                    v=i;
                    k=j;//记录这个点是次短还是最短
                }
            }
        }
        if(v==-1) break;
        vis[v][k]=1;
        for(int i=head[v];i!=-1;i=edge[i].next){
            int j=edge[i].to;
            int dist=d[v][k]+edge[i].w;;
            if(dist<d[j][0]){//dist小于最短路径长。

d[j][1]=d[j][0];//次短路径长
                c[j][1]=c[j][0];//次短路径路径数目
                d[j][0]=dist;//最短路径长
                c[j][0]=c[v][k];//最短路径路径数目
            }
            else if(dist==d[j][0]){//dist等于最短路径长：
                c[j][0]+=c[v][k];//最短路径路径数目
            }
            else if(dist<d[j][1]){//dist大于最短路径长且小于次短路径长：
                d[j][1]=dist;//次短路径长
                c[j][1]=c[v][k];//次短路径路径数目
            }
            else if(dist==d[j][1]){//dist等于次短路径长：
                c[j][1]+=c[v][k];//次短路径路径数目
            }
        }
    }
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        tot=0;
        memset(head,-1,sizeof(head));
        scanf("%d%d",&N,&M);
        int u,v,w;
        for(int i=0;i<M;i++){
            scanf("%d%d%d",&u,&v,&w);
            addEdge(u,v,w);
        }
        int s,g;
        scanf("%d%d",&s,&g);
        Dijkstra(s);
        int res=c[g][0];
        if(d[g][1]==d[g][0]+1){
            res+=c[g][1];
        }
        printf("%d\n",res);
    }
    return 0;
}