Trie图（模板）

Trie图（蒟蒻听说AC自动机能做的题Trie图都能做，而且AC自动机可能被卡，就没学过AC自动机），最近想捡一捡，好久之前做的了。

Trie图，就是一个在Trie树上建的图  大概描述一下

比如说有几个字符串：

abc

abcd

bcd

bacd

jdr

ac

先把它们存在Trie树中：

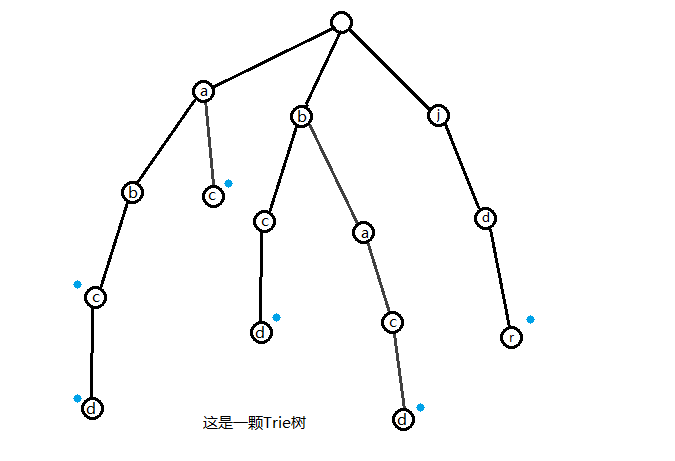
就像KMP那样，做出这样的逻辑判断：

bacd比较到第三位bac结果没有d，但起码bac有了，所以以bac为前缀的或以bac后缀为前缀的串是不用再比较前缀了。

所以出现了fail指针，为失配情况重新定位方案。

类似于next数组。

无解（定位不到失配后新方案），就指向根表示无解。

显而易见，首字母失配是一定没有方案的。

其次，一个字母失配可以定位到父节点失配的自己值子节点。

一个优化：没有新子节点的节点直接指向fail指针自己值子节点。

建出来Trie图是这样的：

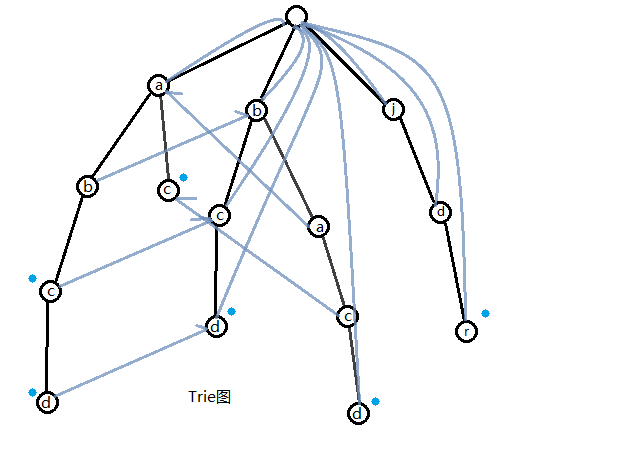
匹配时类似KMP：

模板代码（luogu P3808 【模板】AC自动机（简单版））：

 #include<queue>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 struct trnt{
     int ch[];
     int val;
     int fl;
 }tr[];
 std::queue<int>Q;
 char tmp[];
 int siz;
 int n;
 void add(char *a)
 {
     int len=strlen(a+);
     int root=;
     for(int i=;i<=len;i++)
     {
         int c=a[i]-'a';
         if(!tr[root].ch[c])
             tr[root].ch[c]=++siz;
         root=tr[root].ch[c];
     }
     tr[root].val++;
 }
 void Build()
 {
     int root=;
     for(int i=;i<;i++)
         if(tr[root].ch[i])
             Q.push(tr[root].ch[i]);
     while(!Q.empty())
     {
         root=Q.front();
         Q.pop();
         for(int i=;i<;i++)
         {
             if(tr[root].ch[i])
             {
                 tr[tr[root].ch[i]].fl=tr[tr[root].fl].ch[i];
                 Q.push(tr[root].ch[i]);
             }else
                 tr[root].ch[i]=tr[tr[root].fl].ch[i];
         }
     }
     return ;
 }
 int Cal(char *a)
 {
     int len=strlen(a+);
     int ans=;
     int root=;
     for(int i=;i<=len;i++)
     {
         int c=a[i]-'a';
         root=tr[root].ch[c];
         for(int j=root;j&&(tr[j].val!=-);j=tr[j].fl)
         {
             ans+=tr[j].val;
             tr[j].val=-;
         }
     }
     return ans;
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         scanf("%s",tmp+);
         add(tmp);
     }
     Build();
     scanf("%s",tmp+);
     printf("%d\n",Cal(tmp));
     return ;
 }