LuoguP4012 深海机器人问题(费用流)

题目描述

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。

潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。

用一个P×Q 网格表示深海机器人的可移动位置。西南角的坐标为 (0,0)，东北角的坐标为 (Q,P) 。

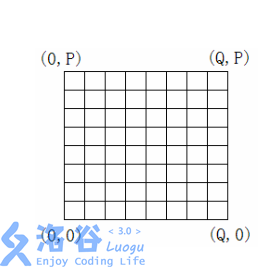
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案， 使深海机器人到达目的地后，采集到的生物标本的总价值最高。

输入输出格式

输入格式：

文件的第 1 行为深海机器人的出发位置数 a,和目的地数 b 。

第 2 行为 P 和 Q 的值。

接下来的 P+1 行,每行有 Q 个正整数,表示向东移动路径上生物标本的价值,行数据依从南到北方向排列。

再接下来的 Q+1 行,每行有 P 个正整数,表示向北移动路径上生物标本的价值,行数据依从西到东方向排列。

接下来的 a 行,每行有 3 个正整数 k,x,y,表示有 k 个深海机器人从 (x,y)位置坐标出发。

再接下来的 b 行,每行有 3 个正整数 r,x,y ,表示有 r 个深海机器人可选择 (x,y)位置坐标作为目的地。

a行和b行输入时横纵坐标要反过来

输出格式：

输出采集到的生物标本的最高总价值.

解题思路：

输入喷我一脸。

在边界建两条流，一条流量为1有费用，一条为0无费用

代码：

 #include<queue>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 const int oo=0x3f3f3f3f;
 struct pnt{
     int hd;
     int pre;
     int lst;
     int dis;
     int val;
     bool vis;
 }p[];
 struct ent{
     int twd;
     int lst;
     int vls;
     int dis;
 }e[];
 int cnt;
 int n,m;
 int s,t;
 int ns,nt;
 int no[][];
 std::queue<int>Q;
 void ade(int f,int t,int v,int d)
 {
     cnt++;
     e[cnt].twd=t;
     e[cnt].vls=v;
     e[cnt].dis=d;
     e[cnt].lst=p[f].hd;
     p[f].hd=cnt;
     return ;
 }
 bool Spfa(void)
 {
     for(int i=;i<=t;i++)
     {
         p[i].dis=p[i].val=oo;
         p[i].vis=false;
     }
     p[t].pre=-;
     p[s].dis=;
     p[s].vis=true;
     while(!Q.empty())
         Q.pop();
     Q.push(s);
     while(!Q.empty())
     {
         int x=Q.front();
         Q.pop();
         p[x].vis=false;
         for(int i=p[x].hd;i;i=e[i].lst)
         {
             int to=e[i].twd;
             if(p[to].dis>p[x].dis+e[i].dis&&e[i].vls>)
             {
                 p[to].dis=p[x].dis+e[i].dis;
                 p[to].val=std::min(p[x].val,e[i].vls);
                 p[to].pre=x;
                 p[to].lst=i;
                 if(p[to].vis)
                     continue;
                 p[to].vis=true;
                 Q.push(to);
             }
         }
     }
     return p[t].pre!=-;
 }
 int Ek(void)
 {
     int ans=;
     while(Spfa())
     {
         ans+=p[t].dis*p[t].val;
         for(int i=t;i!=s;i=p[i].pre)
         {
             e[p[i].lst].vls-=p[t].val;
             e[((p[i].lst-)^)+].vls+=p[t].val;
         }
     }
     return ans;
 }
 int main()
 {
 //    freopen("a.in","r",stdin);
     scanf("%d%d",&ns,&nt);
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             no[i][j]=++cnt;
     s=cnt+;
     t=cnt+;
     cnt=;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<m;j++)
         {
             int x;
             scanf("%d",&x);
             ade(no[i][j],no[i][j+],,-x);
             ade(no[i][j+],no[i][j],,x);
             ade(no[i][j],no[i][j+],oo,);
             ade(no[i][j+],no[i][j],,);
         }
     }
     for(int j=;j<=m;j++)
     {
         for(int i=;i<n;i++)
         {
             int x;
             scanf("%d",&x);
             ade(no[i][j],no[i+][j],,-x);
             ade(no[i+][j],no[i][j],,x);
             ade(no[i][j],no[i+][j],oo,);
             ade(no[i+][j],no[i][j],,);
         }
     }
     for(int i=;i<=ns;i++)
     {
         int a,b,c;
         scanf("%d%d%d",&c,&a,&b);
         ade(s,no[a][b],c,);
         ade(no[a][b],s,,);
     }
     for(int i=;i<=nt;i++)
     {
         int a,b,c;
         scanf("%d%d%d",&c,&a,&b);
         ade(no[a][b],t,c,);
         ade(t,no[a][b],,);
     }
     printf("%d\n",-Ek());
     return ;
 }