机器学习 - 算法 - 集成算法 - 分类 ( Bagging , Boosting , Stacking) 原理概述

Ensemble learning - 集成算法

▒ 目的

让机器学习的效果更好, 量变引起质变

继承算法是竞赛与论文的神器, 注重结果的时候较为适用

集成算法 - 分类

▒ Bagging - bootstrap aggregation

◈ 公式

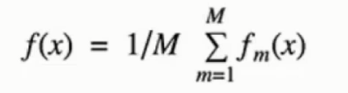
◈ 原理

训练多个分类器取平均, 并行 的训练一堆的分类器

◈ 典例

随机森林

◈ 随机

输入　 -　　数据源采样随机 　　- 　　在原有数据上的进行 60% - 80% 比例的有放回的数据取样

　　　　数据量相同, 但是每个树的样本数据各不相同

特征　 -　　特征选择随机　

　　　　特征的选择加剧随机性

◈ 森林

多个决策树并行放在一起

每个树的特征数一样, 数据量一样

由于二重的随机性(数据集, 特征) ,  每个树基本上都不会一样, 最终的结果也不一样

随机保证了泛化能力, 如果每个树都是一样, 那就无意义了

◈ 优势

能够处理 高纬度  ( feature 很多 ) 的数据, 而且不用做特征选择 (见ps)

在训练后, 可以对  feature 重要程度 进行比对

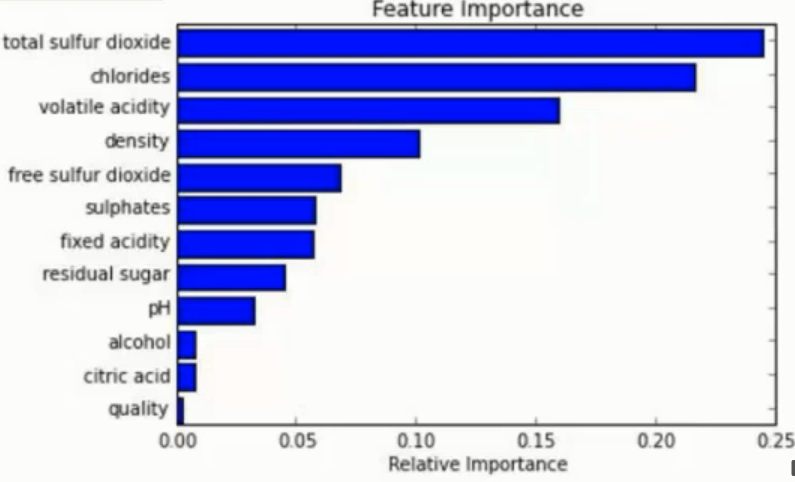
容易做成 并行化 方法, 速度较快

可进行 可视化展示 , 便于分析

◈ ps

特征选择

　　特征选择的目的是为了查找出权重较大对最终结果影响较大的特征

　　比如可以使用将某一特征的数据进行完全破坏再用无用数据填充

　　然后与之前的正常特征数据得到的结果比对从而两个的差值大小判断此特征的有用性

　　也可以建模忽略预测定的某特征进行与带有此特征的进行比对也是相同的道理

　　注意 :  破坏后的特征别用 0 之类的一样的数据进行填充, 完全一样的特征就没意义了

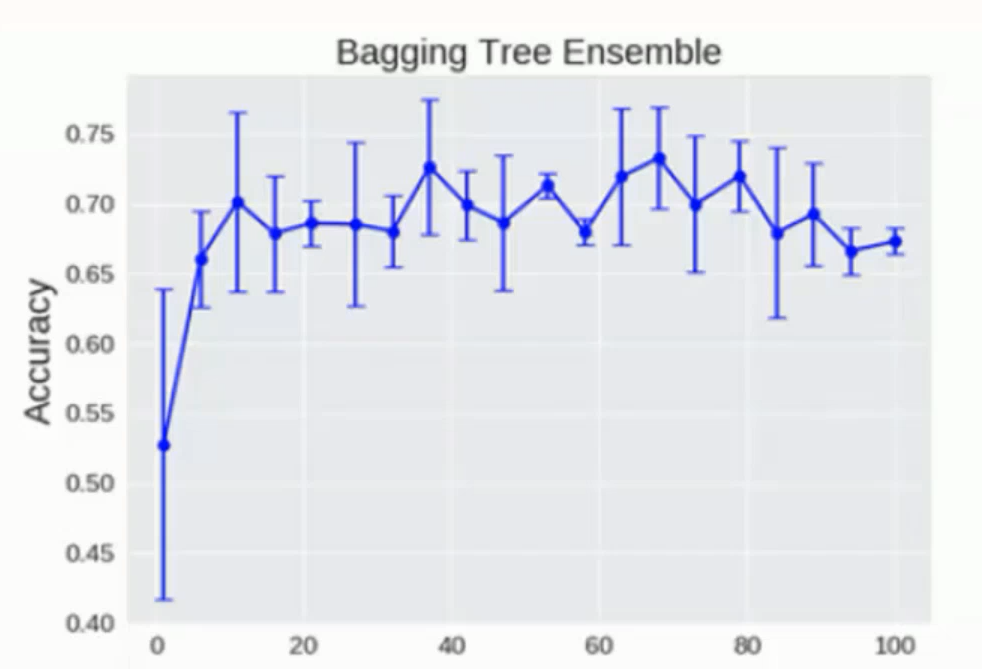
◈ 树模型临界值

随机森林中的树模型理论上是越多越好, 但是其实也会达到临界值

达到一定数量后就会在临界点附近上下浮动

　　

▒ Boosting

◈ 公式 

　　

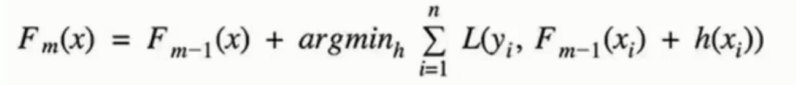
◈ 原理 

串行算法, 后面的树基于前面树的残差计算

从弱学习器开始加强, 通过加权来进行训练 ( 加入一颗比原来强的树 )

例子说明:

　　比如第一颗树预测的结果相差了50, 那么第二颗的任务就是预测这50

　　然后第二颗预测结果是 30 , 与目标又只差了20, 于是第三颗树的任务就是预测剩余的 20

　　以此往下类推, 直到尽可能的填满这50的差值让预测结果和真实结果统一

◈ 典例

AdaBoost

Xgboost    - 详细的内容 点击这里

◈ AdaBoost  原理

根据前一次的分类效果调整数据权重

如果某一个数据分错了, 那么在下一次的分配中会给与更高的权重使其更加精准

最终的结果根据每个分类器自身的准确性确定各自的权重再合并

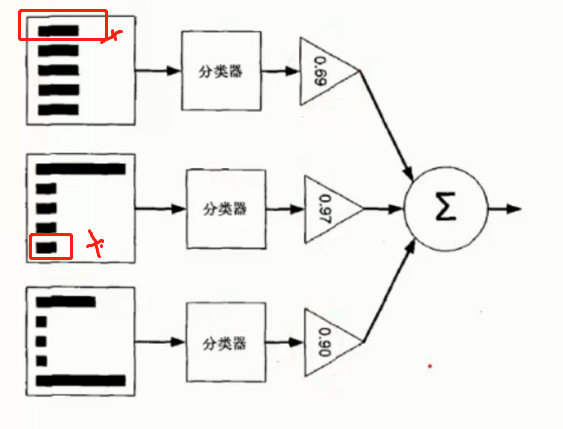
如图所示, 第一个分类器分错了 第一个数据, 因此第二分类器给了第一个数据更高的权重

但是二号又分错了第五个数据, 因此第三个分类器对第五数据更高的权重

▒ Stacking

聚合多个分类或者回归模型. ( 可以分阶段来做 )

◈ 原理

堆叠 直接一堆分类器叠加起来用, 比如有多个算法直接算完了求平均

可以堆叠各种各样的分类器 (KNN, SVM, RF 等等)

分阶段 第一阶段得出各自结果, 第二阶段再用前一阶段的结果来训练

如图, 使用 4 种分类器的结果作为二阶段 LR 分类器的输入再次处理后得到最终结果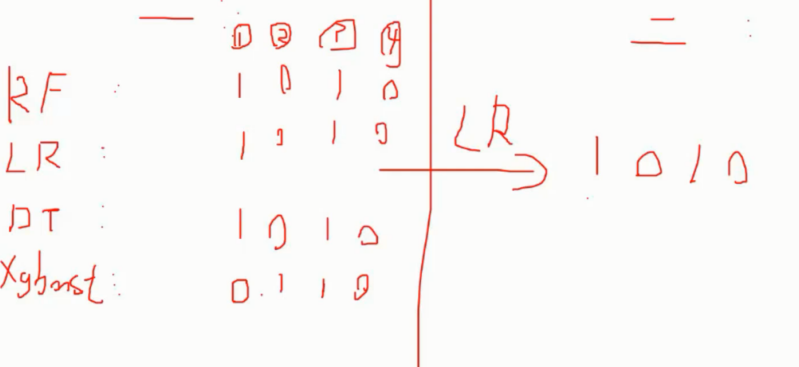

◈ 优势

准确率确实可以提升, 但是速度是个问题