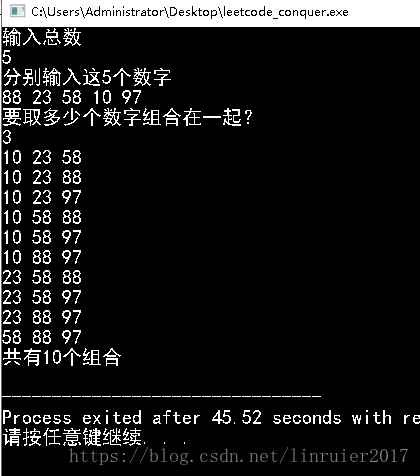
c++回溯法求组合问题（取数，选取问题）从n个元素中选出m个的回溯算法

假如现在有n个数，分别从里面选择m个出来，那么一共有多少种不同的组合呢，分别是哪些呢？

利用计算机的计算力，采用回溯算法很容易求解

程序源代码如下:

#include<iostream>
#include<algorithm>
using namespace std;
bool ok(int get[],int k)
{
for(int i=0;i<k;i++)if(get[i]>=get[k])return false;
return true;
}
void print(int a[],int len)
{
for(int i=0;i<len;i++)
cout<<a[i]<<" ";
cout<<endl;
}
int main()
{
int sum=0;int n,m;
//回溯法从n个数字里面选取m个出来
cout<<"输入总数"<<endl;cin>>n;
int num[n];
cout<<"分别输入这"<<n<<"个数字"<<endl;
for(int i=0;i<n;i++)cin>>num[i];
sort(num,num+n);
cout<<"要取多少个数字组合在一起？"<<endl;
cin>>m;

int get5[m];
for(int i=0;i<m;i++)get5[i]=-1;
int k=0;int c[m];
for(int i=0;i<m;i++)c[i]=0;
while(k>=0)
{
while(c[k]<n)
{
get5[k]=num[c[k]++];
if(ok(get5,k)&&k==m-1)//得到一个完整组合 
{
print(get5,m);sum++;
}
else if(ok(get5,k)&&k<m-1)k++;//得到部分解，继续往下走 
}
get5[k]==-1;
c[k]=0;
k--;
} 
cout<<"共有"<<sum<<"个组合"<<endl;

}