2018南京icpc-J-Prime Game (欧拉筛+唯一分解定理)

题意：给定n个数ai(n<=1e6,ai<=1e6)，定义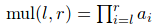，并且fac(l,r)为mul(l,r)的不同质因数的个数，求

思路：可以先用欧拉筛求出1e6以内的所有质数，然后对所有ai判断，如果ai不是质数就利用唯一分解定理计算其所有质因数。然后按照顺序依次计算每个质因子的贡献。假设n=5，对质因子2，依次记录它在数组出现的下标，如果它在2、4下标出现了，那么它的贡献即为所有包含2或4的区间个数，逆向计算，即所有区间个数-不包含2和4的区间个数，即

n(n+1)/2-m1(m1+1)/2-m2(m2+1)/2-m3(m3+1)/2，其中m1=2-1-0=1，m2=3-2=1，m3=5-4=1，即3块不包含2和4的子区间长度。

AC代码：

#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;

typedef long long LL;
const int maxn=1e6+;
int n,a[maxn],cnt,vis[maxn],prime[maxn];
int pre[maxn],vis1[maxn];
LL ans,cs;

void Eular(){
    for(int i=;i<maxn;++i){
        if(!vis[i]) prime[cnt++]=i;
        for(int j=;j<cnt&&i*prime[j]<maxn;++j){
            vis[i*prime[j]]=;
            if(i%prime[j]==) break;
        }
    }
}

void solve(int id,int x){
    if(!vis1[x]){
        vis1[x]=;
        ans+=cs;
    }
    LL t=id--pre[x];
    pre[x]=id;
    ans-=1LL*t*(t+)/;
}

int main(){
    Eular();
    scanf("%d",&n);
    cs=1LL*n*(n+)/;
    for(int i=;i<=n;++i)
        scanf("%d",&a[i]);
    for(int i=;i<=n;++i){
        if(a[i]==) continue;
        if(!vis[a[i]]){
            solve(i,a[i]);
        }
        else{
            int tmp=a[i];
            for(int j=;j*j<=tmp;++j){
                if(tmp%j==){
                    while(tmp%j==) tmp/=j;
                    solve(i,j);
                }
            }
            if(tmp!=){
                solve(i,tmp);
            }
        }
    }
    for(int i=;i<cnt;++i){
        int t=pre[prime[i]];
        if(t){
            t=n-t;
            ans-=1LL*t*(t+)/;
        }
    }
    printf("%lld\n",ans);
}