ML_Review_LDA(Ch5)

Note sth about LDA(Linear Discriminant Analysis)
这篇来说说LDA的复习，LDA在第二次作业的博客中也提及了，但是那是作业思考，所以决定再开一篇只说LDA的。

动机：
  LDA的中文名字——线性判别分析。其主要功能还是降维（N $\rightarrow$ k）。
LDA算法：（用一个二维特征的二分类来说明，因为图好画←_←）
至于多分类，可以参考博客LDA线性分析推广到多分类
  明确LDA是如何进行降维（线性判别的），LDA考虑的和PCA不同之处在于——PCA的样本空间是一个样本，你来做主成分提取；而LDA的样本是一堆样本，你来找轴映射，从而将这些样本分离。于是乎，LDA考虑的目标是——最大化类间距离与最小化类内距离。（即不同类样本尽量离得远，同类尽量离得近）
算法公式概述：

$$ \mu_i = \frac{1}{N_i} \sum_{x \in X_i} x $$
$$ \overline{z_i} = w^T \mu_i = w^T \frac{1}{N_i} \sum_{x \in X_i} x = \frac {1}{N_i} \sum_{x \in X_i} w^Tx $$
Between-calss Scatter：$ J_b = || \overline{z_1} - \overline{z_2} || $
Within-class Scatter：$ J_w = s_1^2 + s_2^2 $，$ s_i = \sum_{z \in Z_i} (z-\overline{z_i})^2 $
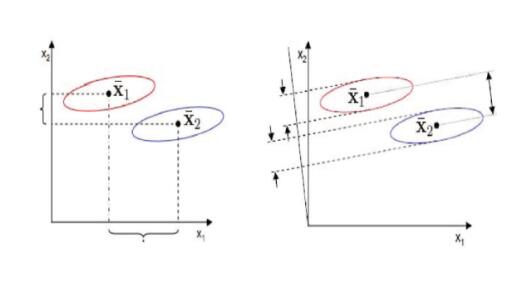
  其实，上式中的$\overline{z_i}$就是$i$这类的中心。即下图中的$\overline{x_i}$，显然右图效果更好，因为左图其实两个类的部分样本映射完已经重叠了。

---

问题：
  显然我们希望最大化$J_b$，而最小化$J_w$，而且是同时的，那么我们应该如何构造我们的优化目标函数？下面提供几个思路：
1、$ arg max J(w) = J_b - J_w $
2、$ arg max J(w) = \frac{J_b}{J_w} = \frac{w^T S_b w}{w^T S_w w} $
  是不是都可以？当$J_b$变大而$J_w$减小的时候，让上述两个值最大，就是我们所需的答案。但是其实$J_b - J_w$是不可以的。因为还要考虑一个问题，虽然$J_b$和$J_w$都是正的，但是谁大谁小我们并不清楚，所以1式是会爆出负数的，而一旦爆出负数，结果就可能会出错，举个例子：$3-100>4-110$，但是$\frac{3}{100}<frac{4}{110}$，显然就出错了。而2因为都是正数，所以可以很好地进行优化。
  紧接着，我们观察一下$ arg max J(w) = \frac{w^T S_b w}{w^T S_w w} $，会发现其实$w$的解是不唯一的，因为如果$w$是解，显然$a*w$也是解，为了方便得解出解，我们添加一个约束，并将问题转化为：$arg max J_b(w) = w^T S_b w$，其中$ w^T S_w w = 1 $，这个和$ arg max J(w) = \frac{w^T S_b w}{w^T S_w w} $是等价的，但是我们可以发现——$arg max J_b(w) = w^T S_b w$，其中$ w^T S_w w = 1 $，又是一个带约束的优化问题，请出Lagrange-multipliers（拉格朗日乘子法）
  我们可以得到：
$$ L(w,\lambda) = w^T S_b w - \lambda(w^T S_w w - 1) $$
$$ \frac{\partial L}{\partial w} = 2S_b w - wS_w w $$
  此时，若$S_w$可逆，则$S_{w}^{-1} S_b w = \lambda w$，又回到了解特征方程的问题，如果$S_w$不可逆呢？我们可以求$S_w$的伪逆，这样问题也是可以解决的。
  关于伪逆，即若$X$与$A^T$同型，且满足：$AXA=A$，$XAX=X$，则$X$为$A$的伪逆矩阵。