【数据结构】P1310 表达式的值

【题目链接】

https://www.luogu.org/problem/P1310

题目描述

对于1 位二进制变量定义两种运算：

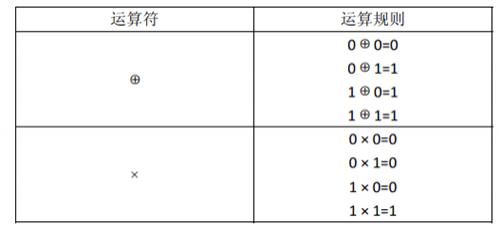
运算的优先级是：

1. 先计算括号内的，再计算括号外的。

2. “× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如_+(_*_)，请你在横线处填入数字00或者11 ，请问有多少种填法可以使得表达式的值为00。

输入格式

共 2 行。

第1 行为一个整数 LL，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 LL 个字符，其中只包含’（’、’）’、’+’、’*’这44 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。

输出格式

共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对1000710007取模后的结果。

输入输出样例

输入 #1

4
+(*)

输出 #1

３

说明/提示

【输入输出样例说明】

给定的表达式包括横线字符之后为：_+(_*_)

在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。

【题解】

1、转变为后缀表达式的形式，然后，如果是操作数要添加一个数字，记住第一个位置要多添加一个‘.’

2、然后进行推导，把四种情况的转移状态写清楚。

参考题解中duyi

第一步：中缀转后缀

后缀表达式是什么呢？参见洛谷P1449

这里先给大家介绍一下中缀表达式转后缀表达式的一般方法：

中缀表达式a + b*c + (d * e + f) * ga+b∗c+(d∗e+f)∗g，其转换成后缀表达式则为a b c * + d e * f + g * +abc∗+de∗f+g∗+。

转换过程需要用到栈，具体过程如下：

1）如果遇到操作数，我们就直接将其输出。

2）如果遇到操作符，则我们将其放入到栈中，遇到左括号时我们也将其放入栈中。

3）如果遇到一个右括号，则将栈元素弹出，将弹出的操作符输出直到遇到左括号为止。注意，左括号只弹出并不输出。

4）如果遇到任何其他的操作符，如（“+”， “*”，“（”）等，从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后，才将遇到的操作符压入到栈中。有一点需要注意，只有在遇到" ) "的情况下我们才弹出" ( "，其他情况我们都不会弹出" ( "。

5）如果我们读到了输入的末尾，则将栈中所有元素依次弹出。

备注：本题中我们用一个"."来代表数字。扫描整个表达式（读入的字符串），如果当前位置不是括号（既不是左括号也不是右括号），就在后缀表达式里填一个"."表示这里应有一个数字。

第二步：DP

状态转移方程很好想：

如果当前是"*"：

f[0][now]=f[0][now]∗f[0][last]+f[0][now]∗f[1][last]+f[1][now]∗f[0][last]

f[1][now]=f[1][now]∗f[1][now]

（注意两式顺序不能颠倒，因为1式中需要用到f[1][now]f[1][now]的原始值）

如果当前是"+":

f[1][now]=f[1][now]∗f[1][last]+f[0][now]∗f[1][last]+f[1][now]∗f[0][last]

f[0][now]=f[0][now]∗f[1][last]

（两式的顺序同样不能颠倒）

其中，f[i][j]表示j号数字是i的情况有多少种，初始化为1

---

【代码】

 #include<bits/stdc++.h>
 using namespace std;
 const int mod =  ;
 const int N = 1e5+;

 int f[][N] ;

 int priority( char s ){
     switch ( s ){
         case '+' : return  ;
         case '*' : return  ;
         case '(' :
         case ')' : return -;
     }
 }

 void toSuffixString( string &s ){
     int len = s.length();

     string res = "." ;
     stack < int > Op ;

     for(int i=;i<len ;i++){
         /*if( s[i] == '.') {
             res += ".";
         }else */
         if( s[i] == '(' || s[i] == '*' ){
             Op.push(s[i]);
         }else if( s[i] == ')' ){
             while( !Op.empty() && Op.top() != '(' ){
                 res += Op.top();
                 Op.pop();
             }
             //出来的时候，栈顶为(.
             Op.pop();
         }else{
             while( !Op.empty() && priority(Op.top()) >= priority(s[i]) ){
                 res += Op.top();
                 Op.pop();
             }
             //出来的时候，栈里面的运算符优先级低于当前位置.
             Op.push( s[i] ) ;
         }
         if( !(s[i] == '(' || s[i] == ')') ){
             res += ".";
         }
     }
     while( !Op.empty() ){
         res += Op.top();
         Op.pop();
     }
     //cout << res << endl ;
     s = res ;
 }

 void Calc( string s ){
     //cout << s << endl ;
     int j =  ;
     int len = s.length();
     for(int i= ; i < len ; i++ ){
         if( s[i] == '.' ){
             j ++ ;
             f[][j] = f[][j] =  ;
         }else if( s[i] == '*' ){
             j -- ;
             f[][j] =(f[][j] * f[][j+] +
                       f[][j] * f[][j+] +
                       f[][j] * f[][j+] ) % mod ;

             f[][j] = (f[][j] * f[][j+]) % mod ;

         }else if( s[i] == '+' ){
             j -- ;
             f[][j] =(f[][j] * f[][j+] +
                       f[][j] * f[][j+] +
                       f[][j] * f[][j+] ) % mod ;

             f[][j] =(f[][j] * f[][j+] ) %mod ;
         }
     }
     cout << f[][] << endl;
 }

 int main(){
     ios_base :: sync_with_stdio( false );
     cin.tie(NULL) , cout.tie(NULL) ;
     int n ;
     string str ;
     cin >> n >> str ;
     toSuffixString(str);
     Calc(str);
     return ;
 }