Jacobi symbol（裸雅可比符号）

Jacobi symbol

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 625    Accepted Submission(s): 258

Problem Description

Consider a prime number p and an integer a !≡ 0 (mod p). Then a is called a quadratic residue mod p if there is an integer x such that x² ≡ a (mod p), and a quadratic non residue otherwise. Lagrange introduced the following notation, called the Legendre symbol, L (a,p):

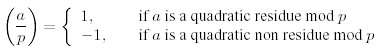
For the calculation of these symbol there are the following rules, valid only for distinct odd prime numbers p, q and integers a, b not divisible by p:

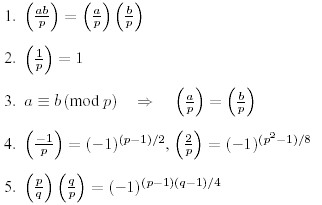
The Jacobi symbol, J (a, n) ,is a generalization of the Legendre symbol ,L (a, p).It defines as :
1.  J (a, n) is only defined when n is an odd.
2.  J (0, n) = 0.
3.  If n is a prime number, J (a, n) = L(a, n).
4.  If n is not a prime number, J (a, n) = J (a, p1) *J (a, p2)…* J (a, pm), p1…pm is the prime factor of n.

 

Input

Two integer a and n, 2 < a< =10⁶，2 < n < =10⁶，n is an odd number.

 

Output

Output J (a,n)

 

Sample Input

3 5
3 9
3 13

 

Sample Output

-1
0
1

 

Author

alpc41

 

Source

2010 ACM-ICPC Multi-University Training Contest（15）——Host by NUDT

/*
题意：裸的雅可比符号，雅可比符号是勒让德符号的延伸，J(a,n)如果n是素数那么J(a,n)=L(a,n);否则J(a,n)=J(a,p1)*J(a,p2)*...J(a,pm);
    p1...pm是n的质因子，勒让德符号：定义为 L(a,n)=0  n mod a=0;
                                           L(a,n)=1  存在X使得 X^2 mod a=0;
                                           L(a,n)=-1 不存在X使得 X^2 mod a=0;
#错误：求雅可比符号的时候，按照定义爆的，不知道哪里错了...分解质因子板套错了

#改进：勒让德符号n是偶数的时候要特判，特别要注意的时候质因子也有偶数，就是2

*/
#include<bits/stdc++.h>
#define ll long long
using namespace std;
/**********************勒让德符号************************/
ll exp(ll a,ll b,ll p)
{
    ll res=;
    for(;b;b>>=)
    {
        if(b&)
        res=(res*a)%p;
        a=(a*a)%p;
    }
    return res;
}

int cal(int a,int n)
{
    if(a%n==)
    return ;
    else
    return exp(a,(n-)/,n)==?:-;
}
/**********************勒让德符号************************/

/***********************筛素数*************************/
const int M = ;
int p[M], pNum=;
bool f[M];

void Prime()
{
    int i, j;
    for(i = ; i < ; i++)
    {
        if(!f[i])//i是素数
        {
            p[pNum++] = i; //将素数打到数组中
        }
        for(j = ; j < pNum && p[j] * i < M; j++ ) //将i的倍数都调出来因为，素数的倍数肯定不是素数
        {
            f[p[j]*i] = ;
            if(!(i%p[j]))
                break;
        }
    }
}
/***********************筛素数*************************/
int a,n;
int cur;
int main(){
    Prime();
    // freopen("in.txt","r",stdin);
    while(scanf("%d%d",&a,&n)!=EOF){
        if(f[n]==){//如果n是素数
            printf("%d\n",cal(a,n));
            continue;
        }
        cur=;
        for(int i=;n!=&&i<pNum;i++){
            if(n%p[i]==){//这个是质因子
                int total=;
                while(n%p[i]==){
                    total++;
                    n/=p[i];
                }
                int tmp=cal(a,p[i]);
                if(total%==&&tmp==-)//如果n里面有偶数个的p，那么p乘偶数肯定不是奇数，就不符合勒让德符号定义了
                    tmp=;
                cur*=tmp;
            }
        }
        printf("%d\n",cur);
    }
    return ;
}