信号处理——卷积（convolution）的实现

作者：桂。

时间：2017-03-07  22:33:37

链接：http://www.cnblogs.com/xingshansi/p/6517301.html

---

前言

信号时域、频域对应关系，及其DFT、FFT等变换内容，在之前的文章1、文章2中已经给出相关的理论推导以及代码实现，本文主要针对信号中常用的卷积进行介绍，内容主要包括：

　　1）卷积的物理意义；

　　2）卷积的直接实现；

　　3）卷积的FFT实现；

　　4）卷积的无延迟快速实现；

本文为自己的学习总结，内容多有参考他人，相关的参考文献名称最后一并给出。

一、卷积的物理意义

知乎上有一段话，非常经典，此处加以引用：

作者：中微子
链接：https://www.zhihu.com/question/20500497/answer/45708002

打个比方，往平静的水面里面扔石头。我们把水面的反应看作是一种冲击响应。水面在t=0时刻石头丢进去的时候会激起高度为h(0)的波纹，但水面不会立马归于平静，随着时间的流逝，波纹幅度会越来越小，在t=1时刻，幅度衰减为h(1), 在t=2时刻，幅度衰减为h(2)……直到一段时间后，水面重复归于平静。

从时间轴上来看，我们只在t=0时刻丢了一块石头，其它时刻并没有做任何事，但在t=1,2….时刻，水面是不平静的，这是因为过去（t=0时刻）的作用一直持续到了现在。

那么，问题来了：

如果我们在t=1时刻也丢入一块石子呢？此时t=0时刻的影响还没有消失（水面还没有恢复平静）新的石子又丢进来了，那么现在激起的波浪有多高呢？答案是当前激起的波浪与t=0时刻残余的影响的叠加。那么t=0时刻对t=1时刻的残余影响有多大呢？

为了便于说明，接下来我们作一下两个假设：

1． 水面对于“单位石块”的响应是固定的

2． 丢一个两倍于的“单位石块”的石块激起的波纹高度是丢一个石块的两倍（即系统满足线性叠加原理）

现在我们来计算每一时刻的波浪有多高：

• t=0时刻：

y(0)=x(0)*h(0);

• t=1时刻：

当前石块引起的影响x(1)*h(0);

t=0时刻石块x(0)引起的残余影响x(0)*h(1);

y(1)=x(1)*h(0)+ x(0)*h(1);

• t=2时刻：

当前石块引起的影响x(2)*h(0);

t=0时刻石块x(0)引起的残余影响x(0)*h(2);

t=1时刻石块x(1)引起的残余影响x(1)*h(1);

y(2)=x(2)*h(0)+ x(1)*h(1)+x(0)*h(2);

……

• t=N时刻：

当前石块引起的影响x(N)*h(0);

t=0时刻石块x(0)引起的残余影响x(0)*h(N);

t=1时刻石块x(1)引起的残余影响x(1)*h(N-1);

y(N)=x(N)*h(0)+ x(N-1)*h(1)+x(N-2)*h(2)+…+x(0)*h(N);

这就是离散卷积的公式了。

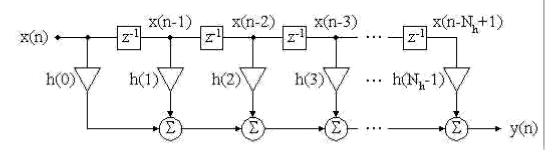
二、卷积的直接实现（Direct convolution）

特点：无延迟、运算量大。

对应公式：

$y(n) = h(0)x(n) + h(1)x(n - 1) + ... + h({N_h} - 1)x(n - {N_h} + 1)$

对应结构图：

对应代码(MATLAB同样有内置指令conv)：

function output_signal=my_direct_convolution(input_signal,impulse_response)
% Input:
%    input_signal: the input signal
%    impulse_response: the impulse response
% Output:
%    output_signal:the convolution result
N=length(input_signal);%define length of signal
K=length(impulse_response);%define length of impulse response
output_signal=zeros(N+K-1,1);%initializing the output vector
xp=[zeros(K-1,1);input_signal;zeros(K-1,1)];
for i=1:N+K-1
    output_signal(i)=xp(i+K-1:-1:i)'*impulse_response;
end

三、卷积的FFT实现

特点：运算量小、需要延迟至少$N_h+N_x$（$N_h$为滤波器长度）个数据点的采样时间。

　　A-卷积与FFT的关系

这里用到一个重要性质：时域卷积等价于各自频域变换相乘。但我们知道，fft或者ifft信号的长度不变，即fft实现的频域相乘，在逆fft（ifft）到时域的结果，实现的是圆卷积，而不是线卷积。

$y(n) = x(n)*h(n)$

对应于频域就是

$Y(k) = X(k) \cdot H(k)$

但$Y(k)、X(k)、H(k)$对应的长度必须一致，且与$y(n)$一致。

为了保持线卷积、圆卷积得到的结果一直，必须在FFT操作之前，适当补零。

举个简单的例子：

x(n) = [2,5,7]; h(n) = [3,4]，求二者的线卷积.

分析：线卷积的结果长度应该为：$N_y = N_x + N_h -1$，即3+2-1.

方法1：直接卷积

y(n) = x(n)*h(n),对应结果（会乘法运算的都能做卷积）：

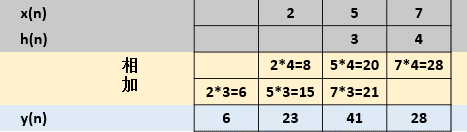
方法2：圆卷积

因为利用FFT操作，对应圆卷积，且x、h长度需要一致，这里我们先取长度为3，看看效果，长度不足3的补零。

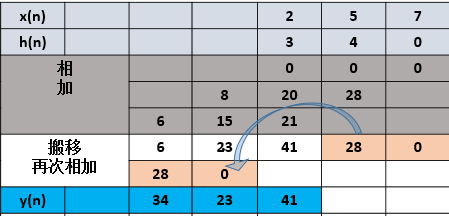
从结果看，结果为{34,23,41}，与结果不一致，可以看到28对应的位置有数值，因此至少取$N_x +N_h$个长度，再来看看结果：

此时已经得出了真实的结果，结论就是：做FFT实现卷积，每一个序列长度补零延长到$N_x +N_h$，则圆卷积与线卷积等价，即FFT运算便可以实现卷积的功能。

　　B-卷积的FFT代码实现

给出对应的代码：

function output_signal=my_fft_convolution(input_signal,impulse_response)
% Input:
%    input_signal: the input signal
%    impulse_response: the impulse response
% Output:
%    output_signal:the convolution result
siglen=length(input_signal);%define the length of signal
implen=length(impulse_response);%define the length of the impulse response
P=siglen+implen-1;%define P
P2=pow2(nextpow2(P));% Find smallest power of 2 that is > P
%%Utilize the code in .pdf
output_signal= real(ifft(fft(input_signal,P2).*fft(impulse_response,P2))); % we need to take the real part to avoid any
% Floating point errors making the output complex
output_signal(P+1:end)=[];%modify the length

给一张直接卷积与FFT卷积的框图：

四、卷积的分段实现

特点：相比于直接卷积，运算量小；相比于FFT实现，延迟量小（$2N_h$，假设数据长度大于滤波器长度）。

　　A-重叠相加法

主要思想：

　　假设每一段长度$N_x$，滤波器长度$N_h$，则每一段线卷积的长度为$N_x+N_h-1$，而每一段长度为$N_x$，故每次移动$N_x$，从而每次的结果后段的$N_h-1$个点重叠相加。核心是利用线卷积的思想，如前文所示，线卷积也可借助FFT快速实现。

对应代码：

function output_signal=my_fast_convolution_add(input_signal,impulse_response)
% Input:
%    input_signal: the input signal
%    impulse_response: the impulse response
% Output:
%    output_signal:the convolution result
siglen=length(input_signal);%define the length of signal
implen=length(impulse_response);%define the length of the impulse response
Nfra=ceil(siglen/implen);%number of frames
%Initialize the output signal
output_signal=zeros(implen*(Nfra+1),1);
%Add zeros
xp=reshape([input_signal;zeros(Nfra*implen-siglen,1)],...
    implen,Nfra);
h=kron(impulse_response,ones(1,Nfra));
%Multiply the ffts together and calculate the ifft
P=pow2(nextpow2(2*implen));%Find smallest power of 2 that is > 2*implen
out_mat=real(ifft(fft(xp,P).*fft(h,P)));
%Overlapping the output blocks and summing
for i=0:Nfra-1
    ni=i*implen+1:i*implen+P;
    output_signal(ni)=output_signal(ni)+out_mat(:,i+1);
end
%Modify the length
output_signal(siglen+implen:end)=[];

　　B-重叠保留法

主要思想：

　　滤波器长度$N_h$，每一段卷积的长度为$2N_h-1$，核心是利用圆卷积的思想，对应频域就是FFT相乘。

举例：

已知$x(n) = n+1,0 \le n \ge 9 $，$h(n) =$ {1,0,-1}，求卷积结果。

直接实现：

$x(n)*h(n) =$ {1 2 2 2 2 2 2 2 2 2 -9 -10} .

重叠相加：

已知$N_h = 3$，长度L最小值为$2N_h-1 = 5$.将$x(n)$分段，得

$x_1(n) =$ {1 2 3 4 5}，$x_2(n) =$ {6 7 8 9 10}，

将每段与$h(n)$卷积：

$y_1 =$ {1 2 2 2 2 -4 -5 },

$y_2 =$ {6 7 2 2 2 -9 -10 }，

重叠$N_h-1 = 2$个点，的

$y =$ {1 2 2 2 2 2 2 2 2 2 -9 -10}

重叠保留：

同样的计算方法，长度最小为5，起始保留$N_h -1 =2$个点，起始补零。

$x_1 =$ {0 0 1 2 3};$x_2 =$ {2 3 4 5 6};

$x_3 =$ {5 6 7 8 9};$x_4 =$ {8 9 10 0 0};

分别与$h(n)$做圆周卷积：

$y_1 =$ {-2 -3 1 2 2};$y_2 =$ {-3 -3 2 2 2};

$y_1 =$ {-3 -3 2 2 2};$y_1 =$ {8 9 2 -9 -10};

丢弃每段最前面的$N_h -1 = 2$个点，为什么这么丢弃，参考前文线卷积与圆卷积的对应关系分析。

$y =$ { 1 2 2 2 2 2 2 2 2 2 -9 -10}.

三种方式完全等价。

这一方法也可以解决输入、输出数据量不匹配的问题：

假设x长度为16，h长度为16，则起始保留Nh-1 = 15个点，起始补零。圆卷积借助FFT实现。重叠相加法也可以实现该功能。

五、卷积的Without Input-output delay实现

特点：无延迟、运算量小。

该方法主要针对滤波器进行分层。

具体可以参考文章：《Efficient convolution without Input-Output Delay》.

下面给出一个自己制作的gif示意图，之前的图片没有了，pdf截图有大有小，拼凑起来凑合看吧，这个图描写了该算法的步骤。

参考：

郑君里：《信号与系统》第二版