[技术]浅谈OI中矩阵快速幂的用法

前言

矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中，矩阵的运算是数值分析领域的重要问题。

基本介绍

（该部分为入门向，非入门选手可以跳过）

由 m行n列元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。

比如一个$m\times n$的矩阵可以表示为：

$$ A=\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
a_{31} & a_{32} & \cdots & a_{3n}\\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix} $$

这$ m\times n$个数称为矩阵的元素，简称为元。数$ a_{ij} $位于矩阵的第i行第j列，称为矩阵的$ (i,j) $ 元，以数$ a_{ij}$为$(i,j)$元的矩阵可记为$(a_{ij})$或$(a_{ij})_{m\times n}$，$m\times n$矩阵A也记为$A_{mn}$

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数和列数都等于n的矩阵称为n阶矩阵或n阶方阵。n阶方阵中所有$i=j$的元素$a_{ij}$组成的斜线称为（主）对角线，所有$i+j=n+1$的元素$a_{ij}$组成的斜线称为辅对角线。

本文讨论的重点运算——矩阵乘

两个矩阵的乘法仅当第一个矩阵A的列数和第二个矩阵B的行数相等时才能定义。如A是$m\times n$矩阵、B是$n\times p$矩阵，他们的乘积C是一个$m\times p$矩阵$c=(c_{ij})$，它的任意一个元素值为：

$$c_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots+a_{i,n}b_{n,j}=\sum_{r=1}^{n}a_{i,r}b_{r,j}$$

并将此乘积记为：$C=AB$。例如：

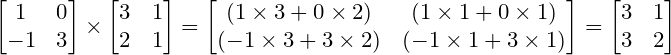
矩阵乘满足结合律、左分配律、右分配律，但是不满足交换律。即：
$(AB)C=A(BC)$

$(A+B)C=AC+BC$

$C(A+B)=CA+CB$

上一波代码：

 struct matrix{
     int data[][];
     matrix operator*(const matrix &a){
         matrix tmp;
         for(int i=;i<;i++)
             for(int j=;j<;j++){
                 tmp.data[i][j]=;
                 for(int k=;k<;k++)
                     tmp.data[i][j]+=data[i][k]*a.data[k][j];
             }
         return tmp;
     }
     matrix operator*=(const matrix &a){
         *this=*this*a;
         return *this;
     }
 };

关于重载什么的，可以参考我的另一篇博文——[技术]浅谈重载操作符

裸乘自然不会怎么出现，OI中，一般都是用的矩阵快速幂，而矩阵快速幂与普通快速幂并没有什么差别，原理也是相同的。

普通快速幂科普：

首先我们考虑，$a^{11}$可以怎样求？

朴素法：$O(n)$，一个一个乘

快速幂：$O(logn)$，$a^{11}=a^{2^{0}+2^{1}+2^{3}}$也就是说，我们只需不断乘上$a^{2^{x}}$即可计算，而这样的计算，可以由指数得到，复杂度为$O(logn)$

代码：

inline int po(int x,int p){
    int ret();
    while(p){
        if(p&)//判断是否为奇数
            ret*=x;
        x*=x;
        p>>=;//除以2
    }
    return ret;
}

那么矩阵快速幂就很简单了

代码如下：

struct matrix{
    int data[][];
    matrix operator*(const matrix &a){
    matrix tmp;
    for(int i=;i<;i++)
        for(int j=;j<;j++){
            tmp.data[i][j]=;
            for(int k=;k<=;k++)
                tmp.data[i][j]+=data[i][k]*a.data[k][j];
        }
        return tmp;
    }
    matrix operator*=(const matrix &a){
        *this=*this*a;
        return *this;
    }
    void identity(){
        memset(data,,sizeof(data));
        for(int i=;i<;i++)
            data[i][i]=;
    }
};
inline matrix pow(const matrix &a,int p){
    matrix tmp;
    tmp.identity();
    while(p){
        if(p&)
            tmp*=a;
        a*=a;
        p>>=;
    }
    return tmp;
}

基本运用

矩阵快速幂可以用来求一些递推关系，比如说最简单的就是斐波那契数列了

我们知道，斐波那契数列的基本递推公式为：

$$f_{i}=f_{i-1}+f_{i-2}$$

那么我们可以设矩阵A和B（其实这玩意儿是向量）：

\[A=\begin{bmatrix} f_{i-1}\\ f_{i-2} \end{bmatrix}\]

\[B=\begin{bmatrix} f_{i}\\ f_{i-1} \end{bmatrix}\]

然后我们的问题就转化为，如何找到一个矩阵X使其能够达到如下转移：

$$B=XA$$

我们考虑矩阵乘法的定义，也就是说，我们要找到一个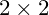的矩阵才能满足前后两个矩阵的行列数（如果一定要说为啥的话，可能会扯一些线性代数什么奇奇怪怪的东西）。那么我们可以设该矩阵X为：

\begin{bmatrix}
a_{11} &a_{12}\\
a_{21} &a_{22}
\end{bmatrix}

那么XA的运算过程为：

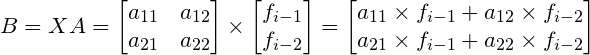
我们令

$$a_{11}\times f_{i-1}+a_{12}\times f_{i-2}=f_{i}$$

$$a_{21}\times f_{i-1}+a_{22}\times f_{i-2}=f_{i-1}$$

由斐波那契数列通项公式:

$$f_{i}=f_{i-1}+f_{i-2}$$

可以解得第一个方程中$a_{11}=1,a_{12}=1$

而显然，第二个方程中，令$a_{21}=1,a_{22}=0$，则等式恒成立

所以解得

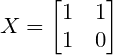
我们再设初始矩阵

那么：

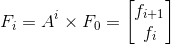
我们就可以轻松地取出斐波那契数了

代码：

 #include<string>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 const int mod=;
 class matrix{
       public:
              int a[][];
              matrix()
              {
                 memset(a,,sizeof(a));
              }
              matrix operator*(matrix &x){
                matrix b;
                for(int i=;i<;i++)
                  for(int j=;j<;j++){
                    b.a[i][j]=;
                    for(int k=;k<;k++)
                      b.a[i][j]+=(a[i][k]*x.a[k][j]);
                      b.a[i][j]%=mod;
                  }
                  return b;
              }
              matrix operator*=(matrix &x){
                *this=*this*x;
                return *this;
              }
 };
 matrix init(){
     matrix res;
     for(int i=;i<;i++)
       for(int j=;j<;j++)
         res.a[i][j]=(i==j);
     return res;
 }
 matrix ks(matrix x,int k){
     matrix res=init();
     while(k){
       if(k&)
         res=res*x;
       k>>=;
       x=x*x;
     }
     return res;
 }
 int n;
 int main(){
     matrix con;
     con.a[][]=;
     con.a[][]=;
     con.a[][]=;
     con.a[][]=;
     matrix f;
     f.a[][]=;
     f.a[][]=;
     while(cin>>n&&n!=-){
       if(n==){
         cout<<<<endl;
         continue;
       }
       if(n==||n==){
         cout<<<<endl;
         continue;
       }
       matrix res=ks(con,n-);
       res*=f;
       cout<<res.a[][]<<endl;
     }
 }

同样的，我们也可以把这种思想转移至其他递推关系中，比如说，我们有以下递推关系：
$$f_{i}=a_{1}f_{i-1}+a_{2}f_{i-2}+\cdots +a_{k}f_{i-k}$$

我们可以用同样的思路求解转移矩阵X，来达到优化求解的目的

比如说上述递推关系的转移矩阵就为：

\begin{bmatrix}
a_{1} & a_{2} & a_{3} & a_{4}& a_{5}\\
1 & 0 & 0 & \cdots & 0\\
0 & 1 & 0 & \cdots & 0 \\
\vdots &\vdots &\vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 & 0
\end{bmatrix}

请读者用项数较小的递推关系证明该矩阵的正确性

进阶

我们有了这样一个工具，但是显然，除非是入门向的裸题，我们首先要能想到矩阵，才能使用它。那么，什么样的题目容易让人想到矩阵呢？

1. 数据范围极大，比如$10^{18}$什么的，$O(n)$都过不去的，可以尝试用矩阵转移
2. 有明显可以使用矩阵快速幂的递推关系的（这个等一会 会说到）
3. 实在想不出来怎么用其他算法，只能乱搞的时候

貌似目前想不到什么了，（可能还是我比较弱，没做过太多题吧）

那么，什么叫明显可以使用矩阵快速幂的递推关系呢？

先上个简单例题：

GT考试

在这道题中，我们忽略字符串因素，（忽略个鬼，就这玩意难），剩下的就是一个很简单的递推，我们发现，该递推关系中，我们用到了加法原理与乘法原理，这是很多递推求方案数的关键点。

我们重新观察一下上述矩阵乘的表达式：

$$c_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots+a_{i,n}b_{n,j}=\sum_{r=1}^{n}a_{i,r}b_{r,j}$$

我们由一步递推开始讨论，设一初始矩阵A：

$$ A=\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\ 
a_{21} & a_{22} & \cdots & a_{2n}\\ 
a_{31} & a_{32} & \cdots & a_{3n}\\ 
\vdots & \vdots & \ddots & \vdots \\ 
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{bmatrix} $$

其中表示由第i种状态一步转移到第j种状态的方案数，那么我们让A平方一下，会发生什么呢？

$$A^{2}$$

$$= \begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
a_{31} & a_{32} & \cdots & a_{3n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{bmatrix}^{2}$$

$$= \begin{bmatrix}
\sum_{r=1}^{n}a_{1r}\times a_{r1} & \sum_{r=1}^{n}a_{1r}\times a_{r2} & \cdots & \sum_{r=1}^{n}a_{1r}\times a_{rn} \\
\sum_{r=1}^{n}a_{2r}\times a_{r1} & \sum_{r=1}^{n}a_{2r}\times a_{r2} & \cdots & \sum_{r=1}^{n}a_{2r}\times a_{rn} \\
\sum_{r=1}^{n}a_{3r}\times a_{r1} & \sum_{r=1}^{n}a_{3r}\times a_{r2} & \cdots & \sum_{r=1}^{n}a_{3r}\times a_{rn} \\
\vdots & \vdots & \ddots & \vdots \\
\sum_{r=1}^{n}a_{nr}\times a_{r1} & \sum_{r=1}^{n}a_{nr}\times a_{r2} & \cdots & \sum_{r=1}^{n}a_{nr}\times a_{rn}
\end{bmatrix}$$

看着这个式子一定还是会十分有点懵，那么我们就拿出平方后的$(1,1)$元来研究。

$(1,1)$元显然等于：

$$\sum_{r=1}^{n}a_{1r}a_{r1}$$

我们感性理解一下，想象当前有n个节点，每两点可以互相到达，并有不同的方案，从节点一经两步回到节点一的方案有多少？

由分类加法原理可得：

$$1\rightarrow 1(two steps)=1\rightarrow 1\rightarrow 1+1\rightarrow 2\rightarrow 1+\cdots +1\rightarrow n\rightarrow 1$$

而由分步乘法原理可得：

$$1\rightarrow x\rightarrow 1=(1\rightarrow x)\times (x\rightarrow 1)$$

那么我们从节点一走两步回到节点一的方案数即为：

$$\sum_{i=1}^{n}(1\rightarrow i)\times (i\rightarrow 1)$$

而$1\rightarrow i$不就是$a_{1i}$吗？所以，当前这个式子的结果，正好是进行矩阵乘之后$a_{11}$的值。

同样的，我们可以把这个结果推广到n步的情况，我们得到初始矩阵之后，用快速幂求解，就可以得到n步之后，各个状态之间的转移情况了。

所以，这可能就是我们常见的运用矩阵快速幂的情况吧。

题表

递推关系（裸题）

GT考试（矩阵&字符串）

五彩的色子

兔农

EX-香蕉（容斥原理）

矩阵幂之和

总结

当出现明显可以使用矩阵解决递推关系时，试着推出递推式

当出现求某种转移方案数时，尝试向矩阵快速幂靠拢，从而使用矩阵

正确理解矩阵，考试不会出裸题，只有想到能用它才是正解，才能将其变成自己的东西

谢谢您的阅读，希望对您有用！