浅读K-means
百度百科释义为
问题
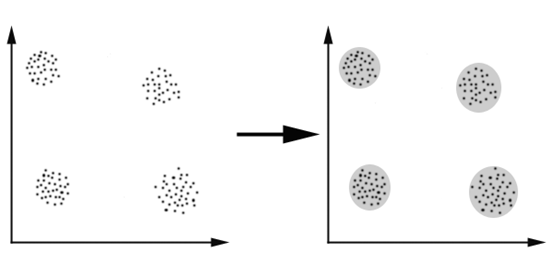

工作原理
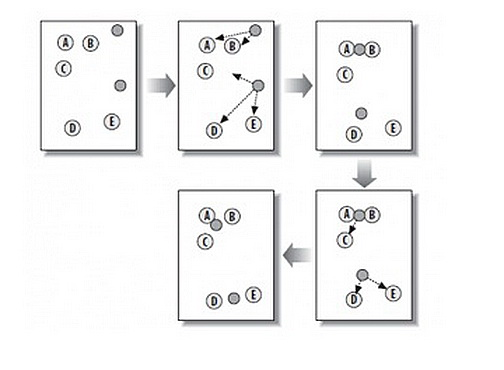 K-Means算法概要
K-Means算法概要工作过程k-means 算法的工作过程
算法优点
算法缺点
浅读K-means的更多相关文章
- Handlebars模板引擎中的each嵌套及源码浅读
若显示效果不佳,可移步到愚安的小窝 Handlebars模板引擎作为时下最流行的模板引擎之一,已然在开发中为我们提供了无数便利.作为一款无语义的模板引擎,Handlebars只提供极少的helper函 ...
- 小王子浅读Effective javascript(一)了解javascript版本
哈哈,各位园友新年快乐!愚安好久没在园子里写东西了,这次决定针对javascript做一个系列,叫做<小王子浅读Effective javascript>,主要是按照David Herma ...
- Spark 源码浅读-SparkSubmit
Spark 源码浅读-任务提交SparkSubmit main方法 main方法主要用于初始化日志,然后接着调用doSubmit方法. override def main(args: Array[St ...
- 浅读tomcat架构设计之tomcat生命周期(2)
浅读tomcat架构设计和tomcat启动过程(1) https://www.cnblogs.com/piaomiaohongchen/p/14977272.html tomcat通过org.apac ...
- 浅读tomcat架构设计之tomcat容器Container(3)
浅读tomcat架构设计和tomcat启动过程(1) https://www.cnblogs.com/piaomiaohongchen/p/14977272.html 浅读tomcat架构设计之tom ...
- 《Attention is All You Need》浅读(简介+代码)
2017年中,有两篇类似同时也是笔者非常欣赏的论文,分别是FaceBook的<Convolutional Sequence to Sequence Learning>和Google的< ...
- 浅谈k短路算法
An Old but Classic Problem 给定一个$n$个点,$m$条边的带正权有向图.给定$s$和$t$,询问$s$到$t$的所有权和为正路径中,第$k$短的长度. Notice 定义两 ...
- 【原理】Java的ThreadLocal实现原理浅读
当前线程的值传递,ThreadLocal 通过ThreadLocal设值,在线程内可获取,即时获取值时在其它Class或其它Method. public class BasicUsage { priv ...
- KNN 与 K - Means 算法比较
KNN K-Means 1.分类算法 聚类算法 2.监督学习 非监督学习 3.数据类型:喂给它的数据集是带label的数据,已经是完全正确的数据 喂给它的数据集是无label的数据,是杂乱无章的,经过 ...
随机推荐
- Spring MVC的实现原理
Spring提供了DispatcherServlet,这个类不仅负责实现请求转发,还负责启动一个WebApplicationContext容器. 按照Spring一贯的IoC哲学,所有的Control ...
- bash中(),{},(()),[],[[]]的区别
前言:在bash中遇到各种括号,同时在进行字符数值比较判定时,总是不断出现问题,于是通过参考<advanced bash-scripting guide>,同时在centos 6.7版本上 ...
- echarts 支持svg格式
今天研究了下echarts的svg格式.发现用ai生成svg格式的图片,echarts上面显示不了. 经过了多次的百度和谷歌终于找到了用Method Draw画出来的svg格式,echarts就能加载 ...
- js判断移动终端(手机浏览器)
方法1: <script type="text/javascript"> var browser = { versions: f ...
- CSS中2d转换:transition过渡放在:hover伪类中与应用在整个元素中区别
css的2d转换十分强大,能够在不使用js的情况下,实现页面的元素与用户之间更多动态的交互,增强用户体验.其中使用最多的就是hover伪类. 1.创建一个页面的div元素: <!DOCTYPE ...
- Jdbc模版式写法与Spring-JdbcTemplate的比较
一.Jdbc模版式写法: [流程] 加载驱动 获取数据库链接 创建Statement对象(用于发送sql语句) 向数据库发送sql语句,获取数据库返回的结果集 从结果集中获取数据 释放资源 上述部分用 ...
- ChromeDriver,IEDriver,Firefox配置
ChromeDriver: 下载ChromeDriver.exe,放入某个文件夹,如C:\Program Files (x86)\Google\Chrome\Application,把此路径加入pat ...
- React Native 系列(八) -- 导航
前言 本系列是基于React Native版本号0.44.3写的.我们都知道,一个App不可能只有一个不变的界面,而是通过多个界面间的跳转来呈现不同的内容.那么这篇文章将介绍RN中的导航. 导航 什么 ...
- ARP协议详解RARP
简单来说,ARP协议是IP地址转换成MAC地址的协议.链路层协议.过程如下: 1:首先,每个主机都会在自己的ARP缓冲区中建立一个ARP列表,以表示IP地址和MAC地址之间的对应关系. 2:当源主机要 ...
- ubuntu中安装搜狗输入法
1.查看系统中是否安装fcitx,libss2-1的依赖包,查看命令 dpkg -I | grep fcitx dpkg -I | grep libssh 没有安装的可以如下图命令安装 2.接下来我 ...
