洛谷2093 JZPFAR + KD-Tree学习笔记 (KD-Tree)

KD-Tree这玩意还真的是有趣啊....

（基本完全不理解）

只能谈一点自己的对KD-Tree的了解了。

首先这个玩意就是个暴力...

他的结构有点类似二叉搜索树

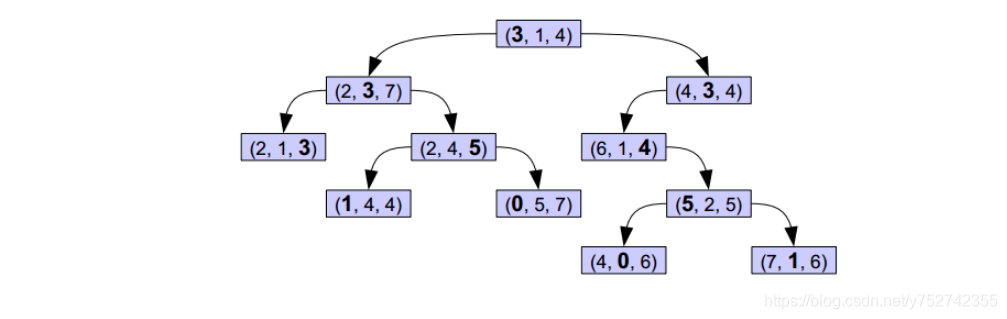
每一层都是以一个维度作为划分标准。

我们对于当前层，选择所有剩余点中，该维度比较中间的那个点作为基准点，比他小（这一维度）就放到左子树，不然右子树。

然后维度的选取是交替选取

就比如说，我们第一层是按照第一个维度，第二层是第二维度，第三层是第一维度....以此类推，直到没有剩余的点为止。

那么构造的时候，由于我们涉及到要把大于某个数的数移动到这个数后面这个操作，这时候就需要一个黑科技！！！！

\[nth_element(a+l,a+x,a+r+1)
\]

这个操作表示我们将\([l,r]\)区间第\(x\)大移动到第\(x\)个位置，然后大于他的放到后面，小于的放到前面

那么这时候其实就比较好解决\(build\)的问题了

void build(int &x,int l,int r,int dd) //建树的时候，我们对于不同的维度，我们选择交替建树，每次选择这个维度里面，值最中间的点作为基准点。
{
    ymh = dd;
    int mid = l+r >> 1;
    x = mid;
    nth_element(t+l,t+x,t+r+1); //将第k大的放到第k个位置，然后比他大的都在前面，小的都在后面
    for (int i=0;i<=1;i++)
      t[x].mx[i]=t[x].mn[i]=t[x].d[i];
    if (l<x) build(t[x].l,l,mid-1,dd^1); //递归处理
    if (r>x) build(t[x].r,mid+1,r,dd^1);
    up(x);
}

那么现在我们该怎么解决\(query\)的问题呢

首先，KD-Tree的询问是不一定复杂度的（可能很高），但是据说是\(\sqrt n\)的？我也不是很确定的

首先，我们要写一个估价函数：

其实这个玩意，就是用来判断这个子树有没有更新答案的可能性

那么既然我们只需要判断可能性，可以直接用一些理论上的东西（比如说子树某一维度的\(mn或者mx\)）

也就说，我们将每个维度和当前询问点差距最大的那个距离加起来，看看是否合法

int calc(int x) //这里这个函数的作用是个估价函数
//如果在一颗子树中，计算理论上的距离当前询问点的最远距离（因为用mn和mx算，所以是理论上）
{
	if(!x) return -100;
	int ans=0;
	for (int i=0;i<=1;i++)
	  ans+=max((t[x].mx[i]-now.d[i])*(t[x].mx[i]-now.d[i]),(t[x].mn[i]-now.d[i])*(t[x].mn[i]-now.d[i]));
    return ans;
}

query的时候，我们每次只需要用当前点更新答案，然后看看需要不需要进入子树里面计算，但是这里有个小\(tips\)，就是

我们进入子树的时候，要选择那个可能性更大子树进入（因为存在进入完更优秀的那个子树之后，另一个子树就没有必要再进去了）

void query(int x)
{
	if (!x) return;
	int dl = calc(t[x].l);
	int dr = calc(t[x].r);
	int d = getdis(t[x],now);
	if (d>q.top().dis || (d==q.top().dis && t[x].num<q.top().num)) //这里用堆维护出最大的k个距离
	{
		q.pop();
		q.push((Node){d,t[x].num});
	}
	if (dl>dr) //之所以要分这个顺序，是因为有可能更新完大的那个子树，就没有必要进入小的子树
	{
		if (dl>=q.top().dis) query(t[x].l); //进入的条件是你的理论距离是大于当前堆顶的（也就是有可能会入堆）
		if (dr>=q.top().dis) query(t[x].r);
	}
	else
	{
		if (dr>=q.top().dis) query(t[x].r);
		if (dl>=q.top().dis) query(t[x].l);
	}
}

那么基本上所有\(KD-Tree\)题的套路部分就这么多了。。

剩下的就是因题而异了

回到这个题。

他要求的是第k大的点对。

那我们这时候就要用一个\(priority_queue\)来维护一个k个值的堆

每次对于一个新的值，我们看是否比当前堆中最小的大，如果大就弹出原来的\(top\)，然后\(push\)新的这个

然后求出来距离尽量大的k个点，最后直接输出\(q.top()\)

不过还是有很多要注意的地方

直接看代码吧

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define mk makr_pair
#define ll long long
#define int long long

using namespace std;

inline int read()
{
  int x=0,f=1;char ch=getchar();
  while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}
  while (isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
  return x*f;
}

const int maxn = 3e5+1e2;
const int inf = 1e18;

struct KD{
    int d[2],mx[2]; //d表示每一维的数是多少，mn表示子树mn，mx表示子树mx
    int mn[2];
    int l,r,num;
};

KD t[maxn],now;

int n,m,root,ymh;

bool operator< (KD a,KD b)
{
    return a.d[ymh]<b.d[ymh]; //便于之后的nth_element的计算
}

void up(int root) //更新信息
{
    for (int i=0;i<=1;i++)
    {
        t[root].mn[i]=min(t[root].mn[i],min(t[t[root].l].mn[i],t[t[root].r].mn[i]));
        t[root].mx[i]=max(t[root].mx[i],max(t[t[root].l].mx[i],t[t[root].r].mx[i]));
    }
}

void build(int &x,int l,int r,int dd) //建树的时候，我们对于不同的维度，我们选择交替建树，每次选择这个维度里面，值最中间的点作为基准点。
{
    ymh = dd;
    int mid = l+r >> 1;
    x = mid;
    nth_element(t+l,t+x,t+r+1); //将第k大的放到第k个位置，然后比他大的都在前面，小的都在后面
    for (int i=0;i<=1;i++)
      t[x].mx[i]=t[x].mn[i]=t[x].d[i];
    if (l<x) build(t[x].l,l,mid-1,dd^1); //递归处理
    if (r>x) build(t[x].r,mid+1,r,dd^1);
    up(x);
}

//上面是KD_Tree问题（

struct Node{
	int dis,num;
}; 

bool operator < (Node a,Node b)
{
	return a.dis>b.dis || ((a.dis==b.dis)&&(a.num<b.num));
}

priority_queue<Node> q;

int getdis(KD a,KD b) //计算两个点之间的距离
{
	return (a.d[0]-b.d[0])*(a.d[0]-b.d[0])+(a.d[1]-b.d[1])*(a.d[1]-b.d[1]);
}

int calc(int x) //这里这个函数的作用是个估价函数
//如果在一颗子树中，计算理论上的距离当前询问点的最远距离（因为用mn和mx算，所以是理论上）
{
	if(!x) return -100;
	int ans=0;
	for (int i=0;i<=1;i++)
	  ans+=max((t[x].mx[i]-now.d[i])*(t[x].mx[i]-now.d[i]),(t[x].mn[i]-now.d[i])*(t[x].mn[i]-now.d[i]));
    return ans;
}

void query(int x)
{
	if (!x) return;
	int dl = calc(t[x].l);
	int dr = calc(t[x].r);
	int d = getdis(t[x],now);
	if (d>q.top().dis || (d==q.top().dis && t[x].num<q.top().num)) //这里用堆维护出最大的k个距离
	{
		q.pop();
		q.push((Node){d,t[x].num});
	}
	if (dl>dr) //之所以要分这个顺序，是因为有可能更新完大的那个子树，就没有必要进入小的子树
	{
		if (dl>=q.top().dis) query(t[x].l); //进入的条件是你的理论距离是大于当前堆顶的（也就是有可能会入堆）
		if (dr>=q.top().dis) query(t[x].r);
	}
	else
	{
		if (dr>=q.top().dis) query(t[x].r);
		if (dl>=q.top().dis) query(t[x].l);
	}
}

signed main()
{
  t[0].mn[0]=t[0].mn[1]=inf;
  t[0].mx[0]=t[0].mx[1]=-inf;
  n=read();
  for (int i=1;i<=n;i++)
  {
  	t[i].d[0]=read();
  	t[i].d[1]=read();
  	t[i].num=i;
  }
  build(root,1,n,1);
  m=read();
  for (int i=1;i<=m;i++)
  {
  	 while (!q.empty()) q.pop();
  	 now.d[0]=read();
  	 now.d[1]=read();
  	 int k=read();
  	 for (int i=1;i<=k;i++)
  	   q.push((Node){-1,-1}); //事先插入k个极小值
  	 query(root);
  	 cout<<q.top().num<<"\n";
  }
  return 0;
}

//https://blog.csdn.net/ws_yzy/article/details/50790735