Leetcode随缘刷题之寻找两个正序数组的中位数

我一上来没读清题，想着这题这么简单，直接就上手写了：

package leetcode.day_12_05;

import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;

/**
 * 给定两个大小分别为 m 和 n 的正序（从小到大）数组nums1 和nums2。请你找出并返回这两个正序数组的 中位数 。
 * <p>
 * 算法的时间复杂度应该为 O(log (m+n)) 。
 * 示例 1：
 * <p>
 * 输入：nums1 = [1,3], nums2 = [2]
 * 输出：2.00000
 * 解释：合并数组 = [1,2,3] ，中位数 2
 * 示例 2：
 * <p>
 * 输入：nums1 = [1,2], nums2 = [3,4]
 * 输出：2.50000
 * 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
 * 示例 3：
 * <p>
 * 输入：nums1 = [0,0], nums2 = [0,0]
 * 输出：0.00000
 * 示例 4：
 * <p>
 * 输入：nums1 = [], nums2 = [1]
 * 输出：1.00000
 * 示例 5：
 * <p>
 * 输入：nums1 = [2], nums2 = []
 * 输出：2.00000
 *
 * @author soberw
 * @Classname FindMedianSortedArrays0004
 * @Description
 * @Date 2021-12-05 21:54
 */
public class FindMedianSortedArrays0004 {
    /**
     * @param array int数组
     * @description: 将int数组转换为List<Integer>
     * @return: List<Integer>
     * @author: soberw
     * @time: 2021/12/5 22:10
     */

    public List<Integer> listOf(int[] array) {
        List<Integer> result = new ArrayList<>();
        for (int i : array) {
            result.add(i);
        }
        return result;
    }

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        double middle = 0.0;
        List<Integer> l1 = listOf(nums1);
        List<Integer> l2 = listOf(nums2);
        l2.addAll(l1);
        l2.sort(Comparator.comparingInt(a -> a));
        if (l2.size() % 2 == 0) {
            middle = ((double) l2.get(l2.size() / 2) + (double) l2.get(l2.size() / 2 - 1)) / 2;
        } else {
            middle = (double) l2.get(l2.size() / 2);
        }
        return middle;
    }
}

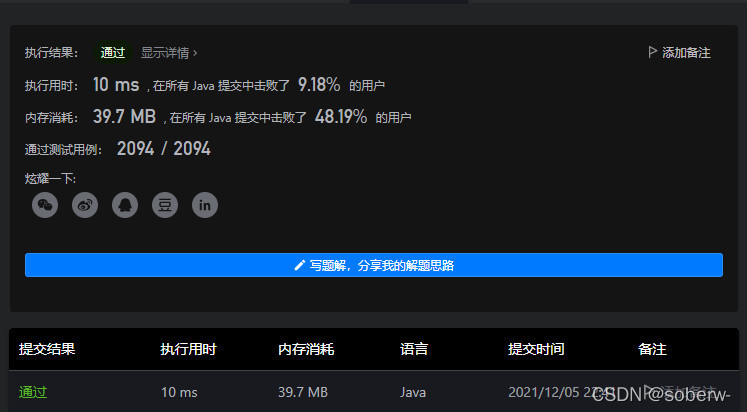
虽然是通过了，但是在我又看一遍题目之后，才发现难点所在。
本题要求时间复杂度控制在O(log(m+n)),而我使用了排序算法就肯定不行了。
因为Arrays.sort时间复杂度是O(nlogn)，光是这就超了。
于是我又想出第二种法：

package leetcode.day_12_05;

/**
 * @author soberw
 * @Classname FindMedianSortedArrays0004
 * @Description
 * @Date 2021-12-05 21:54
 */
public class FindMedianSortedArrays0004_02 {

    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int l1 = nums1.length;
        int l2 = nums2.length;
        //存放合并后的
        int[] num = new int[l1 + l2];
        // 第一个数组索引位置
        int i = 0;
        // 第二个数组索引位置
        int j = 0;
        // 定义的num数组索引位置
        int n = 0;

        //在数组范围内添加元素致新数组
        while (i < l1 && j < l2) {
            if (nums1[i] < nums2[j]) {
                num[n] = nums1[i++];
            } else {
                num[n] = nums2[j++];
            }
            n++;
        }
        // 若其中一个数组已经添加完毕，接下来只需要添加另一个即可
        if (i < l1) {
            for (int a = i; a < l1; a++) {
                num[n++] = nums1[a];
            }
        } else {
            for (int a = j; a < l2; a++) {
                num[n++] = nums2[a];
            }
        }

        //返回中值
        if (num.length % 2 == 0) {
            return ((double) num[num.length / 2] + (double) num[num.length / 2 - 1]) / 2;
        } else {
            return num[num.length / 2];
        }
    }

    public static void main(String[] args) {
        int[] nums1 = {1, 3};
        int[] nums2 = {2, 5};
        System.out.println(new FindMedianSortedArrays0004_02().findMedianSortedArrays(nums1, nums2));
    }
}

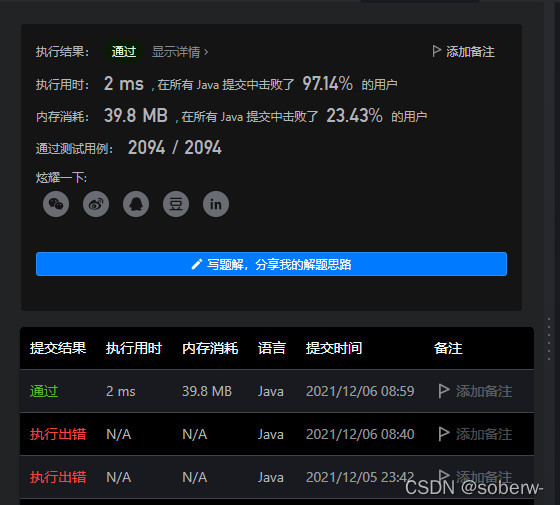
相比于第一种虽然是快了不少，但是时间复杂度还是不够，这次的是O(m+n)。目前这能在先这样了。
欢迎评论区大神指点。