洛谷 P3368 【模板】树状数组 2 题解

P3368 【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的值

输入格式

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

输出格式

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入 #1

5 5

1 5 4 2 3

1 2 4 2

2 3

1 1 5 -1

1 3 5 7

2 4

输出 #1

6

10

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

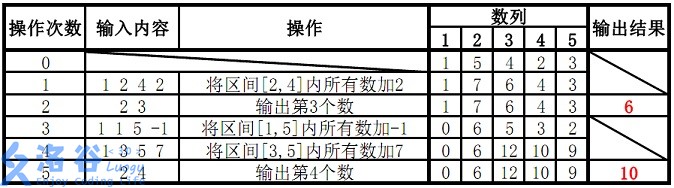
故输出结果为6、10

【思路】

树状数组

【题目大意】

区间修改和单点查询

【题目分析】

明显就是要用线段树的好吧

但是既然是树状数组的模板还是要给他个面子的

所以还得用树状数组写

区间修改和单点查询

第一瞬间想到的时候暴力枚举每一个区间内的点修改

然后求x位置的时候用sum(x) - sum(x - 1)就行了

没有问题

但是这样真的优美吗？

【核心思路】

想要快速修改一个区间的值

除了线段树还有什么呢？

当然是差分了！

差分之后不仅可以用树状数组轻松修改一个区间内的值

而且求某个点的值得时候

也不需要做差

因为在差分数组中1-i的值加起来就是i原本的值

而且sum(x)又是求得1 - x的值

所以很好的可以应用上去

【思路】

#include<iostream>
#include<cstdio>
#define int long long

using namespace std;
const int Max = 500005;
int a[Max];
int n,m;
int read()
{
	int sum = 0,fg = 1;
	char c = getchar();
	while(c < '0' || c > '9')
	{
		if(c == '-')fg = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
	{
		sum = sum * 10 + c - '0';
		c = getchar();
	}
	return sum * fg;
}

int lowbit(int x)
{
	return x & -x;
}

void add(int x,int y)
{
	while(x <= n)
	{
		a[x] += y;
		x += lowbit(x);
	}
}

int sum(int x)
{
	int ans = 0;
	while(x > 0)
	{
		ans += a[x];
		x -= lowbit(x);
	}
	return ans;
}

signed main()
{
	n = read(),m = read();
	int last = 0;
	for(register int i = 1;i <= n;++ i)
	{
		int qwq = read();
		add(i,qwq - last);
		last = qwq;
	}
	for(register int i = 1;i <= m;++ i)
	{
		int qwq = read();
		if(qwq == 1)
		{
			int x = read(),y = read(),z = read();
			add(x,z);
			add(y + 1,-z);
		}
		else
		{
			int x = read();
			cout << sum(x) << endl;
		}
	}
	return 0;
}