长乐国庆集训Day5

T1 方阵

题目

【题目描述】

小澳最近迷上了考古，他发现秦始皇的兵马俑布局十分有特点，热爱钻研的小澳打算在电脑上还原这个伟大的布局。

他努力钻研，发现秦始皇布置兵马俑是有一定规律的。兵马俑阵总共有n行m列，秦始皇在布置的时候每次会指定一行或一列，然后指定一个兵种，使得这一行或者这一列上全部放上这一个兵种。如果这一行上以前放过其它的兵种，那么他会拔掉以前的兵种改成现在他命令的兵种。

小澳从秦朝的文献中找到了布置这个方阵的操作顺序，他希望你能告诉他布局完成后整个兵马俑阵是什么样子的。

【输入格式】

输入文件共q+1行。

输入文件第1行包括三个正整数n,m,q，分别表示兵马俑阵的行数和列数以及秦始皇总的操作数。

接下来q行，每行三个正整数x,y,z，x表示操作种类，若x=1表示给第y行(y≤n)全部放上z这个兵种，若x=2，则表示给第y列(y≤m)全部放上z这个兵种，数据保证z≤2³¹-1。

【输出格式】

n行，每行m个整数，分别用空格隔开。表示最后方阵上每个位置放的兵种，如果某个位置没有被操作过输出0。

【输入样例】

【输出样例】

【数据规模】

对于前20%的数据，n×m≤25。

对于前30%的数据，q≤2000。

对于100%的数据，n,m≤1000，n×m≤10⁵，q≤10⁶。

解析

惊！原题长乐培训Day4t1！

送分题，直接模拟即可，不过得从后往前来，不然会超时。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

struct rec{

    int p,x,y;

}s[];

int n,m,q,map[][];

int main()

{

    //freopen("matrix.in","r",stdin);

    //freopen("matrix.out","w",stdout);

    int t;

    n=read(),m=read(),q=read();

    for(int i=;i<=q;i++) s[i].p=read(),s[i].x=read(),s[i].y=read();

    for(int i=q;i>=;i--)

    {

        if(s[i].p==)

        {

            for(int j=;j<=m;j++)

                if(!map[s[i].x][j]) map[s[i].x][j]=s[i].y;

        }

        else

        {

            for(int j=;j<=n;j++)

                if(!map[j][s[i].x]) map[j][s[i].x]=s[i].y;

        }

    }

    for(int i=;i<=n;i++)

    {

        for(int j=;j<=m;j++) cout<<map[i][j]<<" ";

        cout<<endl;

    }

    return ;

}

T2 排名

题目

【题目描述】

小明班里一共N名同学，小明这次考试考的不错，他知道他考了多少分，以及班级里的同学一共考了多少分，小明还知道这次考试满分为100，问小明最高可以排第几，最低可以排第几。

（相同分数算并列的排名，比如总共4个人7,6,6,5，那么他们的排名分别就是1,2,2,4）

【输入格式】

第一行包括三个整数N,A,S，分别表示班里同学的人数，小明的分数，以及班里同学的总分。

【输出格式】

包括两个用空格隔开的正整数，分别表示小明在最优情况下的排名，以及在最坏情况下的排名。

【输入样例】

【输出样例】

【数据规模】

对于40%的数据，1≤N≤10；

对于100%的数据，1≤N≤10⁵，0≤A≤100，0≤S≤100N。

解析

贪心：

计算最高排名时，先将所有人分数定为a，如果总分不够或总分刚好够，则第1；如果够，则逐渐增加满分人数，直到总分不够或刚好够，则排名为满分人数+1。

计算最低排名时，先将所有人分数定为a+1，如果总分不够，则排名为当前分数为a+1的总人数+1；如果够，则排名为n。

注意a=100分的情况(此时a+1=101，超出满分)，特判一下直接输出即可。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

int n,a,s,num;

int high(int ans)

{

    for(int i=;i<=n;i++)

    {

        if(ans>=a) ans-=a;

        else return ;

    }

    if(ans==) return ;

    for(int i=;i<=n;i++)

    {

        if(ans>=-a) ans-=-a;

        else return i;

        if(ans==) return i;

    }

    return n;

}

int low(int ans)

{

    for(int i=;i<n;i++)

    {

        if(ans>=a+) ans-=a+;

        else return i;

    }

    return n;

}

int main()

{

    //freopen("rank.in","r",stdin);

    //freopen("rank.out","w",stdout);

    n=read(),a=read(),s=read(),s-=a;

    if(a==) cout<<"1 1";

    else cout<<high(s)<<" "<<low(s);

    return ;

}

T3 最长不下降子序列

题目

【题目描述】

给你一个正整数N，请你统计出所有的长度恰好为n的01序列的最长不下降子序列之和。

【输入格式】

第一行包括一个正整数N。

【输出格式】

一行包括一个整数表示所统计的答案，由于答案可能会很大，所以我们把答案对10⁹+7取模。

【输入样例】

【输出样例】

【数据规模】

对于30%的数据，n≤20；

对于100%的数据，n≤200。

解析

DP题，令f[i][j][k]表示长度为i，以0结尾的最长不下降子序列长度为j,以1结尾的最长不下降子序列长度为k的方案数，初值均为0，边界f[1][1][0]=f[1][0][1]=1。

状态转移方程：考虑给第i+1位上填0或1。

若第i+1位上填0，则f[i+1][j+1][k]+=f[i][j][k]，第i+1位为0，只能由第i位为0时得到。
若第i+1位上填1，则f[i+1][j][max(j,k)+1]+=f[i][j][k]，第i+1位为1，无论第i位是0还是1，其以1结尾的最长不下降子序列长度必然增加，因为1是最大的，故k取max(j,k)+1。

最终答案为max(j,k)*f[n][j][k]之和。

Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

const int mod=;

int n;

long long ans,f[][][];//f[i][j][k]表示长度为i,以0结尾最长不降子序列长度为j,以1结尾为k

int main()

{

    //freopen("lis.in","r",stdin);

    //freopen("lis.out","w",stdout);

    f[][][]=,f[][][]=;

    cin>>n;

    for(int i=;i<=n;i++)

        for(int j=;j<=i;j++)

            for(int k=;k<=i;k++)

            {

                f[i+][j+][k]=(f[i+][j+][k]+f[i][j][k])%mod;

                f[i+][j][max(j,k)+]=(f[i+][j][max(j,k)+]+f[i][j][k])%mod;

            }

    for(int j=;j<=n;j++)

        for(int k=;k<=n;k++) ans=(ans+(long long)max(j,k)*f[n][j][k])%mod;

    cout<<ans;

    return ;

}

T4 奇袭

题目

【题目描述】

给出一张N×N的网格图，一共有N支军队驻扎在一些网格中（不会有两只军队驻扎在一起）。

每有一个k×k(1≤k≤N)的子网格图包含恰好k支军队，袭击的难度就会增加1点，请你计算出袭击的难度。

【输入格式】

第一行，一个正整数N，表示网格图的大小以及军队数量。

接下来N行，每行两个整数X_i,Y_i，表示第i支军队的坐标。

保证每一行和每一列都恰有一只军队，即每一个X_i和每一个Y_i都是不一样的。

【输出格式】

一行，一个整数表示袭击的难度。

【输入样例】

【输出样例】

【数据规模】

对于前10%的数据，N≤100；

对于前40%的数据，N≤5000；

对于100%的数据，N≤50000。

解析

以下来源于出题人的题解。

对于每一个坐标(x,y)，记b[x]=y，故所求为序列b满足下列条件的区间[l,r]的数量：

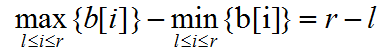
Code

#include <algorithm>

#include <iostream>

#include <cstring>

#include <string>

#include <cstdio>

#include <cmath>

using namespace std;

int read()

{

    int num=,w=;

    char ch=getchar();

    while(ch<''||ch>'')

    {

        if(ch=='-') w=-;

        ch=getchar();

    }

    while(ch>=''&&ch<='')

    {

        num=(num<<)+(num<<)+ch-'';

        ch=getchar();

    }

    return num*w;

}

const int N=,M=;

int n,a[N],maxl[N],maxr[N],minl[N],minr[N],bz[M*];

long long work(int l,int r)

{

    if(l==r) return ;

    int mid=(l+r)>>;

    maxl[mid]=minl[mid]=a[mid],maxr[mid+]=minr[mid+]=a[mid+];

    for(int i=mid-;i>=l;i--) maxl[i]=max(maxl[i+],a[i]),minl[i]=min(minl[i+],a[i]);

    for(int i=mid+;i<=r;i++) maxr[i]=max(maxr[i-],a[i]),minr[i]=min(minr[i-],a[i]);

    long long t=;

    for(int i=mid;i>=l;i--)

    {

        int p=i+maxl[i]-minl[i];

        if(p<=mid||p>r) continue;

        if(minr[p]>minl[i]&&maxr[p]<maxl[i]) t++;

    }

    for(int i=mid+;i<=r;i++)

    {

        int p=i-maxr[i]+minr[i];

        if(p>mid||p<l) continue;

        if(minl[p]>minr[i]&&maxl[p]<maxr[i]) t++;

    }

    int z1=mid+,z2=mid;

    for(int i=mid;i>=l;i--)

    {

        while(minr[z2+]>minl[i]&&z2<r) z2++,bz[maxr[z2]-z2+M]++;

        while(maxl[i]>maxr[z1])

        {

            bz[maxr[z1]-z1+M]--,z1++;

            if(z1>r) break;

        }

        if(z1>r) break;

        if(z1<=z2) t+=bz[minl[i]-i+M];

    }

    for(int i=mid;i>=l;i--) bz[minl[i]-i+M]=;

    for(int i=mid+;i<=r;i++) bz[maxr[i]-i+M]=;

    z1=mid,z2=mid+;

    for(int i=mid+;i<=r;i++)

    {

        while(minl[z2-]>minr[i]&&z2>l) z2--,bz[maxl[z2]+z2+M]++;

        while(maxr[i]>maxl[z1])

        {

            bz[maxl[z1]+z1+M]--,z1--;

            if(z1<l) break;

        }

        if(z1<l) break;

        if(z2<=z1) t+=bz[minr[i]+i+M];

    }

    for(int i=mid+;i<=r;i++) bz[minr[i]+i+M]=;

    for(int i=mid;i>=l;i--) bz[maxl[i]+i+M]=;

    return t+work(l,mid)+work(mid+,r);

}

int main()

{

    n=read();

    for(int i=;i<=n;i++)

    {

        int x=read(),y=read();

        a[x]=y;

    }

    cout<<work(,n);

    return ;

}