洛谷 P4017 最大食物链计数 题解

P4017 最大食物链计数

题目背景

你知道食物链吗？Delia生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。

题目描述

给你一个食物网，你要求出这个食物网中最大食物链的数量。

（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）

Delia非常急，所以你只有1秒的时间。

由于这个结果可能过大，你只需要输出总数模上80112002的结果。

输入格式

第一行，两个正整数n、m，表示生物种类n和吃与被吃的关系数m。

接下来m行，每行两个正整数，表示被吃的生物A和吃A的生物B。

输出格式

一行一个整数，为最大食物链数量模上80112002的结果。

输入输出样例

输入 #1

5 7

1 2

1 3

2 3

3 5

2 5

4 5

3 4

输出 #1

5

说明/提示

各测试点满足以下约定：

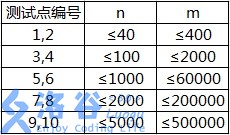
【补充说明】

数据中不会出现环，满足生物学的要求。（感谢@AKEE ）

【思路】

记忆化搜索

一开始我想DP然后失败了

不过貌似记忆化搜索很好想

所以我就来尝试了一哈

没有问题

【吐槽】

（和食物链的代码几乎一样）

（黄题食物链不是另一道）

模数为80112002

我觉得是出题人的生日是20021108吼

有意思

【题目大意】

有向图，找完整的链的数目

(完整的链的意思是：

链的头不能有入边，链的尾不能有出边)

【题目分析】

上面已经说过

一条完整的链就是链的头不能有入边

链的尾不能有出边

因为如果还有的话那就是还有可以被吃或者吃的

那这条食物链就没有结束

就不能算是一条食物链

（学过生物食物链那一部分知识的的应该都知道）

所以搜索的时候就有了目标

从头开始搜，因为头要满足没有入边

所以在建图的时候记录入度和出度

然后如果这个点没有入度

那就是可以搜的

但是还是有一个条件的

他必须要有出度才能搜

不然就成了一个没有入度也没有出度的点

也就是一种孤立的生物

所以必须满足没有入度并且有出度

这样同时也可以避免把孤立的生物算进来

这样搜索肯定是要超时的

所以就要考虑优化

【优化】

剪枝？不现实

没一条边都有可能参与到食物链的构建中去

所以剪枝的话没有剪枝的条件

那就记忆化搜索吧

反正每个点之后会有多少条食物链都是一定的

那就开一个数组记录每个点之后有多少条食物链

这样如果数组里面有值

那就直接加上就好了

否则就搜一下然后记录起来

【完整代码】

#include<iostream>
#include<cstdio>
#define int long long
#define mo 80112002
using namespace std;
const int Max = 200010;
struct node
{
	int y,ne;
}a[Max << 2];
int head[Max >> 1],sum = 0;
void add(int x,int y)
{
	a[++ sum].y = y;
	a[sum].ne = head[x];
	head[x] = sum;
}
int ru[Max >> 2],chu[Max >> 2];
int dp[Max >> 2];
int ans = 0;

int dfs(int x)
{
	if(dp[x] != 0)return dp[x];
	int ans = 0;
	if(ru[x] != 0 && chu[x] == 0)
		ans ++;
	for(register int i = head[x];i != 0;i = a[i].ne)
	{
		ans += dfs(a[i].y);
	}
	dp[x] = ans % mo;
	return ans % mo;
}

signed main()
{
	freopen("food.in","r",stdin);
	int n,m;
	cin >> n >> m;
	int a,b;
	for(register int i = 1;i <= m;++ i)
	{
		cin >> a >> b;
		add(a,b);
		chu[a] ++;
		ru[b] ++;
	}
	int tot = 0;
	for(register int i = 1;i <= n;++ i)
		if(ru[i] == 0 && chu[i] != 0)
			tot += dfs(i) % mo;
	cout << tot % mo << endl;
	return 0;
}