使用协方差矩阵的特征向量PCA来处理数据降维

取2维特征，方便图形展示

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data = load_iris()
y = data.target
X = data.data
pca = PCA(n_components=2)
reduced_X = pca.fit_transform(X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
for i in range(len(reduced_X)):
    if y[i] == 0:
        red_x.append(reduced_X[i][0])
        red_y.append(reduced_X[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_X[i][0])
        blue_y.append(reduced_X[i][1])
    else:
        green_x.append(reduced_X[i][0])
        green_y.append(reduced_X[i][1])
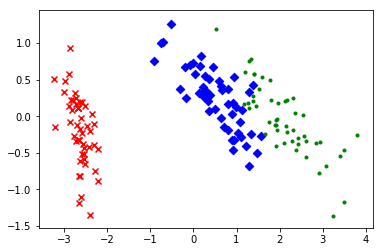
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()