codeforces 508B

B. New Year Permutation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Examples

input

75 2 4 3 6 7 10001001000000000000101000001000000000100001001000

output

1 2 4 3 6 7 5

input

54 2 1 5 30010000011100100110101010

output

1 2 3 4 5

Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).

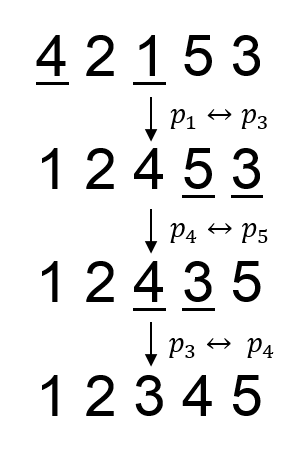
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).

A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.

题意：给你一个数字n，然后底下n个数字，然后再给你n排01串，01串的意思是如果第i行第j列的数字是1，那么上面的数字串里的第i个数字和第j个数字就可以交换位置，题目保证m[i][j] = m[j][i]，问你按照这么操作下来（如果m[i][j] = 1,那么A[i]与A[j]可交换，也可不交换），能得到的数字串最小的字典序是多少

思路：dfs

#include <iostream>
using namespace std;

int m[400][400];
int g[400];
bool vis[400];
int x;
int t,it;
bool flag[400];
int w[400];
//dfs的目的是得到x可以的最小值
void dfs( int a ){
	if( !vis[g[a]] ){//如果说g[a]没有遍历过，那么取小的值
		x = min( x,g[a] );
	}
	w[a] = it;//然后第a个数字，就用过了，防止下面出现死循环
	for( int i = 0; i < t; i++ ){
		if( m[a][i] == 1 and w[i] != it ){//搜索可能出现的最小值
			dfs(i);
		}
	}
}

int main(){
	cin >> t;
	for( int i = 0; i < t; i++ ){
		scanf("%d",&g[i]);
	}
	for( int i = 0; i < t; i++ ){
		for( int j = 0; j < t; j++ ){
			scanf("%1d",&m[i][j]);
		}
	}
	for( int i = 0; i < t; i++ ){
		it++;//记录是第几个数字
		x = t;//先令x的序号为最大
		dfs(i);
		vis[x] = true;
		printf("%d ",x);
	}
}

好多大佬用的是floyd算法，仔细研究了一下dalao的代码，受益匪浅啊～

#include <iostream>
using namespace std;
const int maxn = 400;
bool vis[maxn];
int A[maxn],m[maxn][maxn];
int a;
int pos[maxn];

int main(){
	cin >> a;
	for( int i = 1; i <= a; i++ ){
		cin >> A[i];
		pos[A[i]] = i;//离散化,这不操作可以即可以根据数字找到位置，也可以根据位置找到数字
	}
	for( int i = 1; i <= a; i++ ){
		for( int j = 1; j <= a; j++ ){
			scanf("%1d",&m[i][j]);
		}
		m[i][i] = 1;//自己与自己交换是被允许的
	}

	for( int k = 1; k <= a; k++ ){// floyd一下
		for( int i = 1; i <= a; i++ ){
			for( int j = 1; j <= a; j++ ){
				if( m[i][k] == 1 and m[k][j] == 1 ){
					m[i][j] = 1;
				}
			}

		}
	}
	//i代表i号位置，j代表数字j
	for( int i = 1; i <= a; i++ ){//这个循环是循环数组
		for( int j = 1; j <= a; j++ ){
			if( m[i][pos[j]] == 1 and !vis[j] ){//因为pos[j]是j的位置，j又是从小到达的，这步贪心
				cout << j << " ";
				vis[j] = true;//j这个数字用过了
				pos[A[i]] = pos[j];//改变A[i]的位置为j的位置（A[i]与j位置互换）
				pos[j] = i;//j的位置变成了i
				break;
			}
		}
	}
}