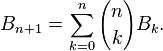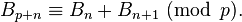贝尔数(来自维基百科)& Stirling数
贝尔数
贝尔数以埃里克·坦普尔·贝尔(Eric Temple Bell)为名,是组合数学中的一组整数数列,开首是(OEIS的A000110数列):
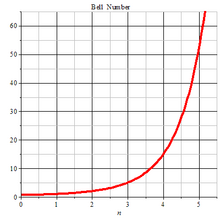
Bell Number
Bn是基数为n的集合的划分方法的数目。集合S的一个划分是定义为S的两两不相交的非空子集的族,它们的并是S。例如B3 = 5因为3个元素的集合{a, b, c}有5种不同的划分方法:
- {{a}, {b}, {c}}
- {{a}, {b, c}}
- {{b}, {a, c}}
- {{c}, {a, b}}
- {{a, b, c}};
B0是1因为空集正好有1种划分方法。空集的每个成员都是非空集合(这是Vacuous truth,因为空集实际上没有成员),而它们的并是空集本身。所以空集是它的唯一划分。
贝尔数适合递推公式:
上述组合公式的证明:
可以这样来想,B_{n+1}是含有n+1个元素集合的划分的个数,考虑元素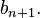
假设他被单独划分到一类,那么还剩下n个元素,这种情况下划分个数为 ;
;
假设他和某一个元素被划分为一类,那么还剩下n-1个元素,这种情况下划分个数为 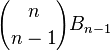 ;
;
假设他和某两个元素被划分为一类,那么还剩下n-2个元素,这种情况下划分个数为  ;
;
依次类推,得到了上述组合公式
它们也适合“Dobinski公式”:
它们也适合“Touchard同余”:若p是任意质数,那么
每个贝尔数都是"第二类Stirling数"的和
Stirling数S(n, k)是把基数为n的集划分为正好k个非空集的方法的数目。
把任一概率分布的n次矩以首n个累积量表示的多项式,其系数和正是第n个贝尔数。这种数划分的方法不像用Stirling数那个方法粗糙。
贝尔数的指数母函数是
贝尔三角形[编辑]
用以下方法建构一个三角矩阵(形式类似杨辉三角形):
- 第一行第一项是1(
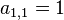 )
) - 对于n>1,第n行第一项等同第n-1行最后一项。(
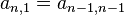 )
) - 对于m,n>1,第n行第m项等于它左边和左上方的两个数之和。(
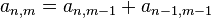 )
)
结果如下:(OEIS:A011971)
每行首项是贝尔数。每行之和是第二类Stirling数。
这个三角形称为贝尔三角形、Aitken阵列或Peirce三角形(Bell triangle, Aitken's array, Peirce triangle)。
参见[编辑]
参考[编辑]
贝尔数(来自维基百科)& Stirling数的更多相关文章
- 自然数幂和——第一类Stirling数和第二类Stirling数
第一类Stirling数 首先设 $$S_k(n)=\sum_{i=0}^ni^k$$ 根据第一类斯特林数的定义(P是排列数,C是组合数,s是Stirling) $$C_n^k={P_n^k\over ...
- arp:地址解析协议(Address Resolution Protocol)(来自维基百科)
地址解析协议(Address Resolution Protocol),其基本功能为通过目标设备的IP地址,查询目标设备的MAC地址,以保证通信的顺利进行。它是IPv4中网络层必不可少的协议,不过在I ...
- web框架--来自维基百科
- Bell(hdu4767+矩阵+中国剩余定理+bell数+Stirling数+欧几里德)
Bell Time Limit:3000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status ...
- 第一类和第二类Stirling数
做了老是忘…… 实际问题: 找维基百科.百度百科…… 第一类Stirling数 n个元素构成m个圆排列 S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m) 初始 S(0,0)=1 S(n ...
- [总结] 第二类Stirling数
上一道例题 我们来介绍第二类Stirling数 定义 第二类Stirling数实际上是集合的一个拆分,表示将n个不同的元素拆分成m个集合的方案数,记为 或者 .和第一类Stirling数不同的是,集合 ...
- Stirling数
第一类: 定义 第一类Stirling数表示表示将 n 个不同元素构成m个圆排列的数目.又根据正负性分为无符号第一类Stirling数 和带符号第一类Stirling数 .有无符号Stir ...
- Bell数和Stirling数
前面说到了Catalan数,现在来了一个Bell数和Stirling数.什么是Bell数,什么是Stirling数呢?两者的关系如何,有用于解决什么算法问题呢? Bell数是以Bell这个人命名的,组 ...
- Stirling数入门
第一类Stirling数 定义 $$\begin{aligned}(x)_n & =x(x-1)...(x-n+1)\\&= s(n, 0) + s(n,1)x +..+s(n,n)x ...
随机推荐
- 浅析软件工程中的UML建模技术
一.基本信息 标题:浅析软件工程中的UML建模技术 时间:2018 出版源:电子世界 领域分类:软件工程:UML建模技术:需求分析 二.研究背景 问题定义:软件工程中UML建模技术的研究 难点:明确软 ...
- Nginx+Tomcat反向代理利用certbot实现https
一.利用Let's Encrypt 免费生成HTTPS证书 1.下载安装certbot(Let's Encrypt ) 2.利用certbot生成证书 3.配置nginx的https证书 安装cerb ...
- 多态&虚函数
(1).对象类型: a.静态类型:对象声明时的类型,编译的时候确定 b.动态类型:对象的类型是运行时才能确定的 class A {}; class B:pub ...
- Instruments Time Profiler时,无法定位代码,如何破?
都是地址符号,往深里也一直是地址符号,根本没法判断是哪些代码的执行时间 解决办法: 选下面的.
- MySQL性能调优与诊断
* 本篇随笔为<涂抹MySQL>一书的阅读摘抄,详细请查看正版书籍 关键性指标 IOPS(Input/Output operations Per Second) 每秒处理的I/O请求次数 ...
- python 使用进程池Pool进行并发编程
进程池Pool 当需要创建的子进程数量不多时,可以直接利用multiprocessing中的Process动态成生多个进程,但如果是上百甚至上千个目标,手动的去创建进程的工作量巨大,此时就可以用到mu ...
- 软件包管理之rpm与yum
软件包的安装和卸载时很平常的事,但在Linux上面却不简单..Linux的其中一个哲学就是一个程序只做一件事,并且做好.组合小程序来完成复杂的任务,这样做有很多好处,但是各个小程序之间往往会存在着复杂 ...
- nginx代理tomcat做负载
先对三台服务器统一环境. 对两台tomcat服务器的操作 查看jdk环境 # java -version openjdk version "1.8.0_65" OpenJDK Ru ...
- javaScript 物体多形态改变加回调函数
小方块同时改变 width height top left opacity(透明度) 加回调函数 改变第二个方块. 效果如下: <!DOCTYPE html> <html lang ...
- Java运行环境(win10)
系统安装Java后,配置运行环境,我的系统是win10,之前随便装了,没想到最近执行javac命令报错,(网上找了一堆都没用)处理方式如下: 环境变量-新建:变量名:%JAVA_HOME% 变量值: ...