【JVM】-NO.114.JVM.1 -【JDK11 HashMap详解-3-put-treeifyBin()-AVL】

Style：Mac

Series：Java

Since：2018-09-10

End：2018-09-10

Total Hours：1

Degree Of Diffculty：5

Degree Of Mastery：5

Practical Level：5

Desired Goal：5

Archieve Goal：3

Gerneral Evaluation：3

Writer:kingdelee

Related Links：

http://www.cnblogs.com/kingdelee/

https://www.jianshu.com/p/65c90aa1236d

https://www.cnblogs.com/zhangbaochong/p/5164994.html

http://www.cnblogs.com/skywang12345/p/3577479.html

https://blog.csdn.net/qq_25806863/article/details/74755131

https://blog.csdn.net/skyroben/article/details/72824146

1.在put的时候，当节点数>=7时，会执行进化树结构，调用treeifyBin(tab, hash)

for (int binCount = 0; ; ++binCount) {
                    if ((e = p.next) == null) {
                        logger.info("p.next为空，为其创建新的节点，p.next.hash:" + hash + ", p.next.value:" + value);
                        p.next = newNode(hash, key, value, null); // 将当前的节点的下一个节点指向新创建的节点
                        if (binCount >= TREEIFY_THRESHOLD - 1) // 只有>=7次迭代才会执行进化树结构
                        {
                            logger.info("binCount >= (TREEIFY_THRESHOLD - 1), binCount:" + binCount + ", (TREEIFY_THRESHOLD - 1):" + (TREEIFY_THRESHOLD - 1));
                            treeifyBin(tab, hash);
                        }
                        logger.info("跳出循环");
                        break;
                    }
                    if (e.hash == hash &&
                            ((k = e.key) == key || (key != null && key.equals(k)))){
                        logger.info("同一个对象");
                        break;
                    }
                    logger.info("p.next有值, p.next.hash：" +  p.next.hash + ",p.next.value:" + p.next.value + ", 把当前p指针指向p.next");
                    p = e;
                }

　　

2. 每次在同坑位的节点>=7的情况下，但凡put节点进来都会进行一次扩容

所以，在容量小于64时，在当同坑位的节点>=7，每递增一个节点，进行一次扩容

当容量大于64时，进化树结构。

final void treeifyBin(Node<K,V>[] tab, int hash) {
        int n, index; Node<K,V> e;
        logger.info("n = tab.length:" + tab.length);
        if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) //小于最小默认树结构容量64时进行扩容
        {
            logger.info("小于树最小容量阀值64，进行扩容");
            resize();
        }
        else if ((e = tab[index = (n - 1) & hash]) != null) {
            TreeNode<K,V> hd = null, tl = null;
            do {
                TreeNode<K,V> p = replacementTreeNode(e, null);
                if (tl == null)
                    hd = p;
                else {
                    p.prev = tl;
                    tl.next = p;
                }
                tl = p;
            } while ((e = e.next) != null);
            if ((tab[index] = hd) != null)
                hd.treeify(tab);
        }
    }

　　

3.说说树

为毛要用树这种结构？

原理引用：1.有序数组虽然查询快插入慢，而链表插入快但是查询慢；

而树的查找效率如下，层数是遍历次数，时间复杂度 O(logN)

以下源自《Java数据结构和算法（第二版）》

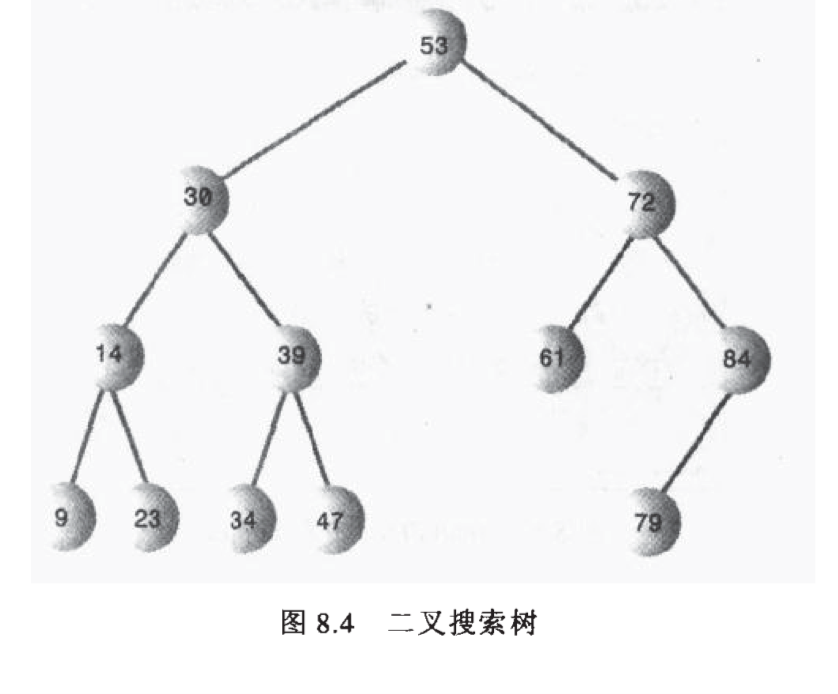
红黑树

必须满足4个规则：

1.每一个节点不是红色就是黑色

2.根总是黑色

3.若节点时红色，则其子节点一定是黑

4.从根到叶节点或非空子节点的每条路径，必须包含相同数量的黑色节点

5.每个叶节点（NIL，即正常情况下的最后一个节点的1个或2个隐式节点）都是黑的

3.AVL

平衡检测

高度(height)：从根节点(root)开始到某一个叶子节点(leaf)的最长路径(path)上结点的个数

平衡因子(balanced factor)：某个结点的平衡因子等于该节点的左孩子的高度减去右孩子的高度

根据平衡树的定义，计算得到的平衡因为会出现两种情况：

• 如果平衡因子是0, 1, -1 这三个数的话，可以认定该节点是符合平衡树的定义的；
• 否则，该结点不平衡，需要重新平衡；

对于一个BST来说，每次插入的元素只可能放在叶子结点上。所以只能影响某个子树是否平衡，对其他子树不会有任何的影响。在这种情况下，我们只需要根据搜索的路径，从孩子往祖先找，如果有不平衡的结点就可以被找到。如果一直到根结点都没有发现不平衡结点，则可以认为这次的插入操作没有造成树的不平衡。

重平衡

如果发现了某个不平衡的结点，那么就需要对该结点进行重平衡。实现重平衡的方法，是对该节点的子树进行旋转(rotation)。

把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

1.对α的左儿子的左子树进行一次插入

2.对α的左儿子的右子树进行一次插入

3.对α的右儿子的左子树进行一次插入

4.对α的右儿子的右子树进行一次插入

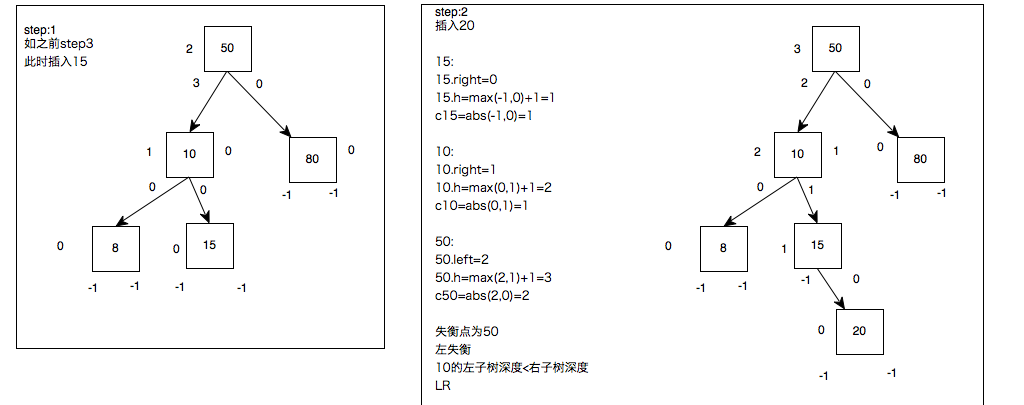
举例：

1.最初的AVL

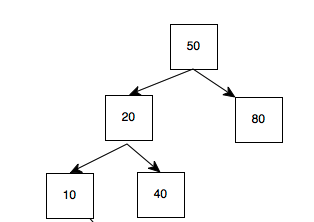
50先插入，50为根；再插入的20比50小，故应插入50左下，作为50的左子树；再插入的80比50大，故应插入50的右下，作为50的右子树；

插入10，比50小，左下，比20小，左下；插入40，比50小，左下，比20大，右下；

故，这图为，50为根，50的左子树是以20为根的子树(20,10,40....)，50的右子树以80为根的子树

50的左子树长度是20->10，即2；右子树长度为1；2-1=1，符合平衡树的差值；这是一个AVL树

此时，倘若只要左子树再增加一个长度（即插入诸如2，12，30，45等）

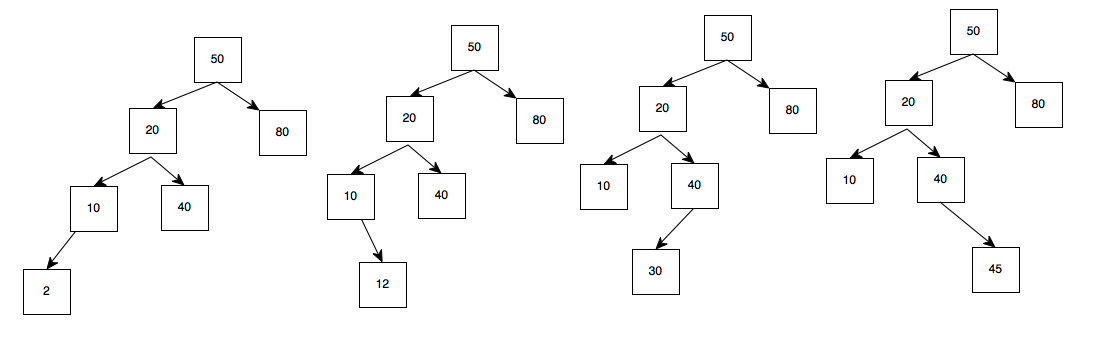
50的左子树的长度变为3，而右子树的长度为1，差值为2而不是小于等于1，此时，不符合AVL树的要求。

故在AVL的规范下，需要对此时的非AVL做调整形成AVL树

对其中（添加2或12）此种，左子树(20->10>2或20->40->30)比右子树(80)的路径>1，且是在最后一层(10, 40)的左边，称为：LL左左

对其中（添加30或45）此种，左子树(20->40>30或20->40->45)比右子树(80)的路径>1，且是在最后一层(10, 40)的右边，称为：LL左右

对于LL左左的旋转操作：

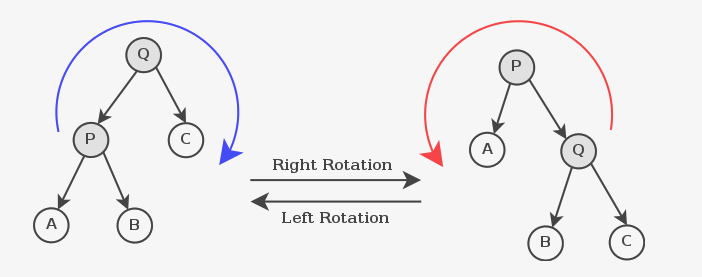
左旋：操作如下图【最好用谁强大谁上位来理解，否则用旋转理解，谁旋谁死；见过有硬硬解释旋转的，还用通过逆顺时针来解释的，勉强多看几次是能看懂但不好理解会忘；绝无仅有，申请专利，将xx旋转更名为Lee上位:)】

白话左旋就是，50根失去左平衡，受不了左边20的压力就断开与左20的连接；20成功上位，但是不能不管曾经的老大根，所以，把旧老大作为自己的右小弟(右子树)；只能有一个右小弟呐，新老大20认为旧老大50好歹也做过老大经验丰富，就把自己的小弟40丢给旧老大50左他的小弟。完。左旋一点都不好理解，应理解为哪边失衡（变强大），哪边就要上位了。

所以ll左左如下，左左是其他变形的基础，其他都是变形的理解都是建立在这个东西之上的。

------------------------------------

对于LR左右：

我们采取和之前上位一样的操作

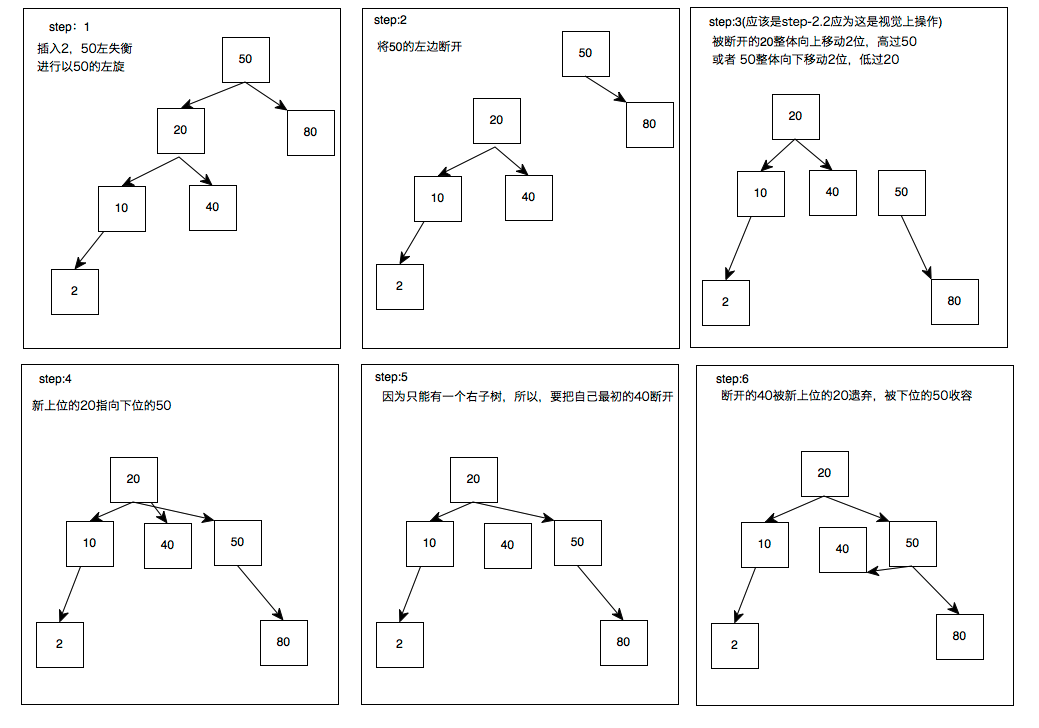
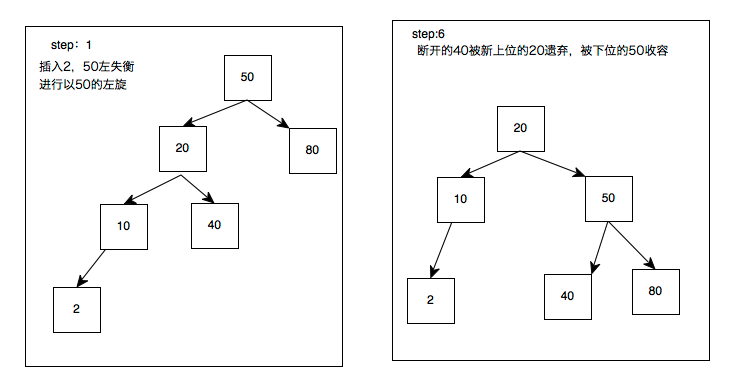
50的左子树失衡，断开与20的连接；20上位，右边重连50，把40丢给50持有。

发现仍失衡

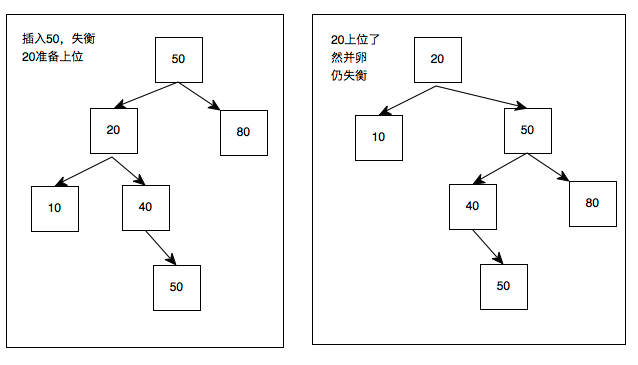
为毛在10底下的新节点就行，为在40底下的新节点就不行?啊咧，仅有这样的区别的话，想办法形成和之前的最初的左左的图一样不就可以了吗

于是：

20上位行不通，40上位试一试。

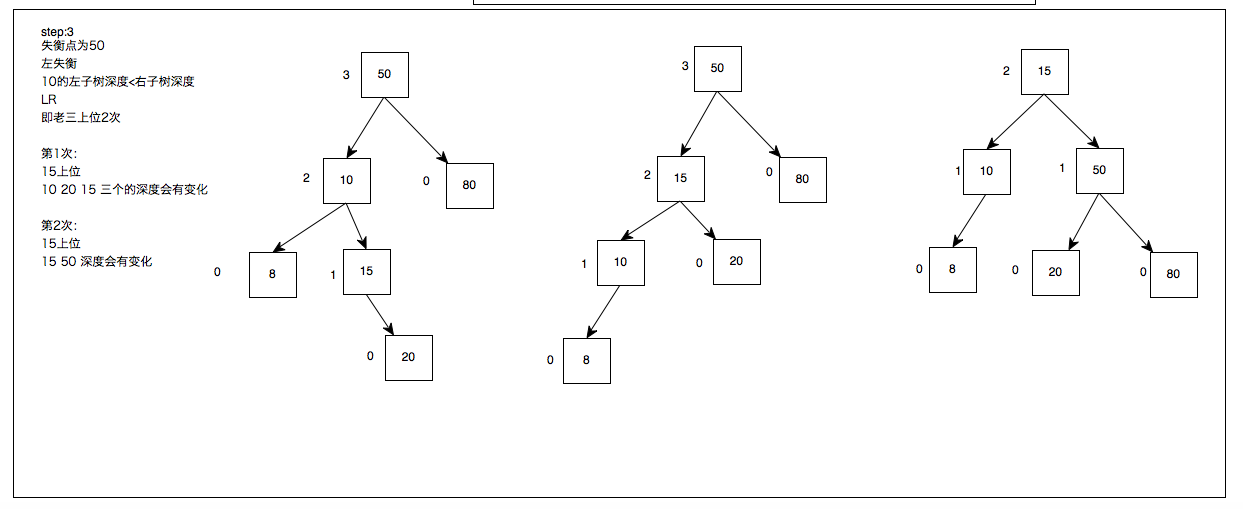
第一次上位：验算中发现20太弱尝试做老大是失败的（这一步不需要实操），20的小弟40要上位；20断开与50的连接，40上位20；40与50产生连接成为新的小王；20被40收容做小弟。可是仍没平衡呐，但是出现LL形状了，胜利就在眼前，40可以采取LL的方式继续上位

第二次上位：和LL一样，40断开与50的连接上位，50成为40的小弟；40把自己的小弟45丢给前老大50收容，AVL了

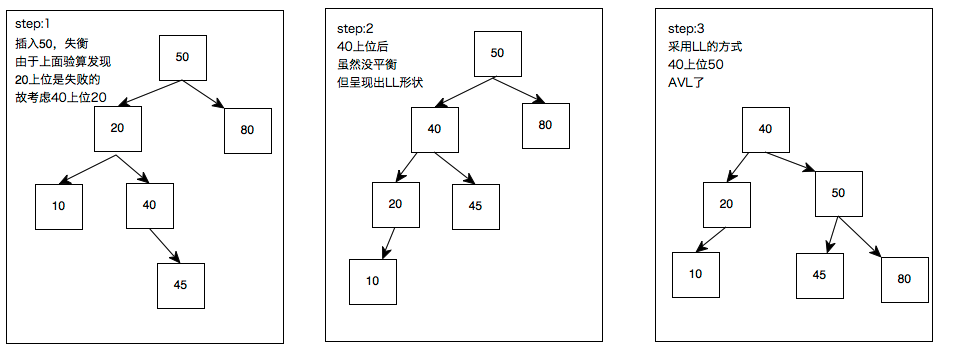
以上解决了LL和LR两种图形

结论是：

1.当发现新加入的节点造成根出现左子树失衡，且新加入的节点是在叶节点（最后一层）的左节点上，即为LL；老二上位1次即可

2.当发现新加入的节点造成根出现左子树失衡，且新加入的节点是在叶节点（最后一层）的右节点上，即为LR；老三上位2次即可

----------------------------------------------------

如果AVL是这样子的，插入以下新的节点都会导致AVL失衡，和上面很像了

同理，1、2是RL，3、4是RR

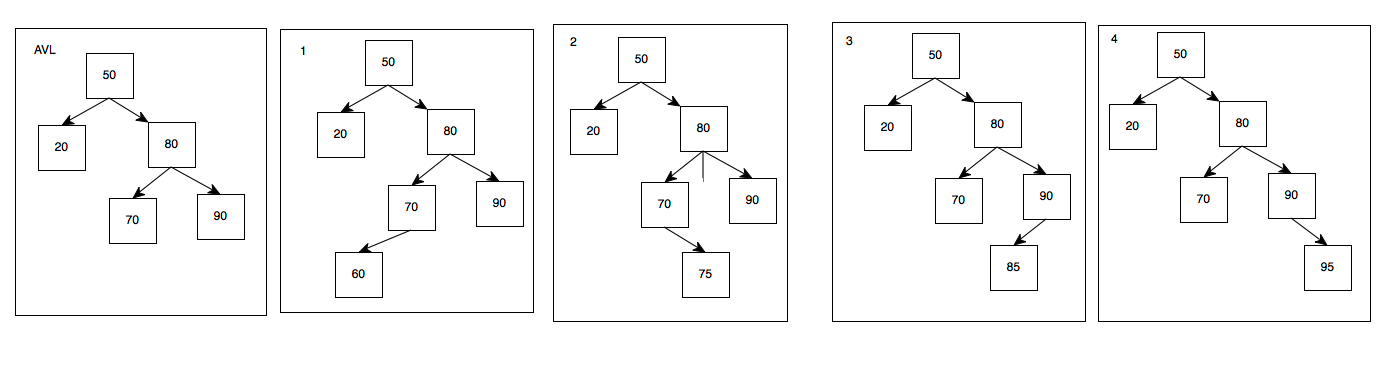
先看3、4的RR，这个是基础

RL呢

跟之前是类似的

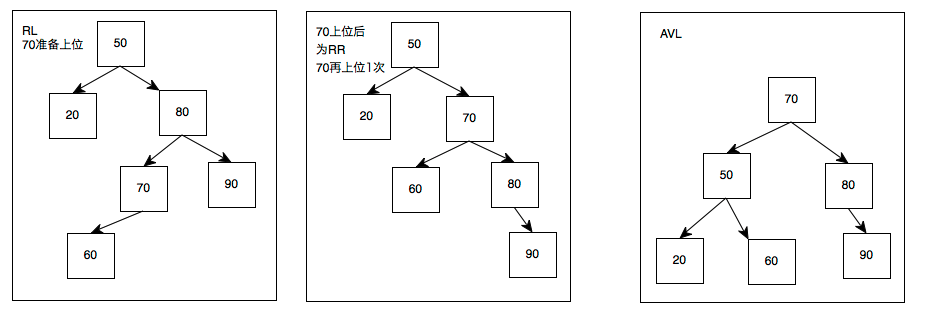
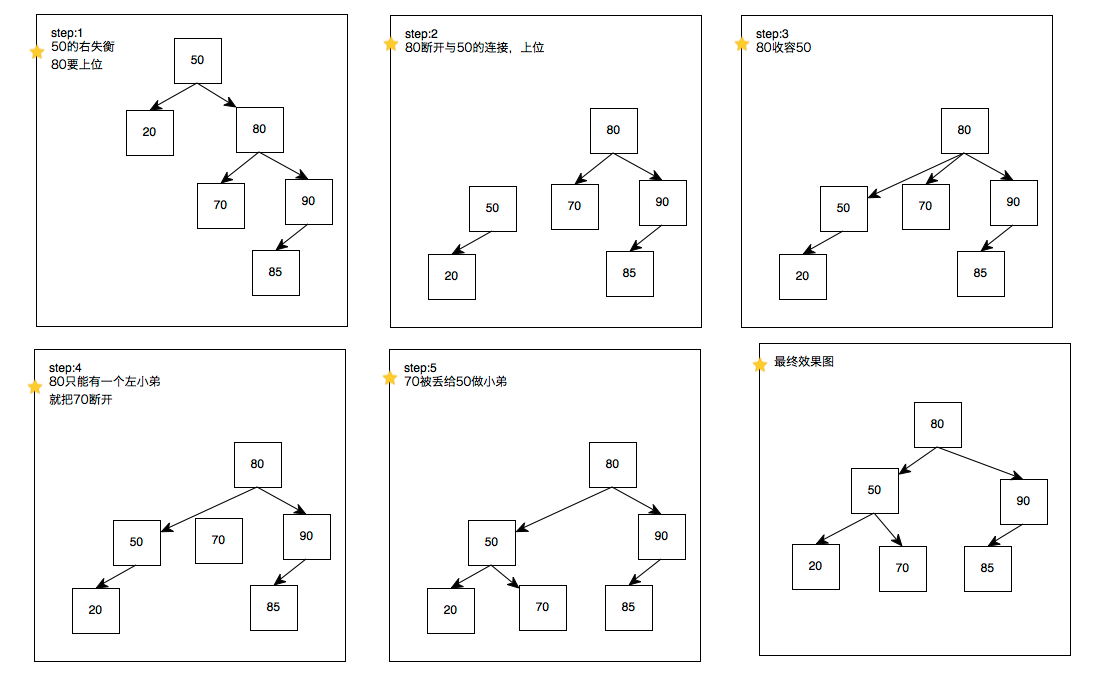
可是，以上仍然不够严谨

因为

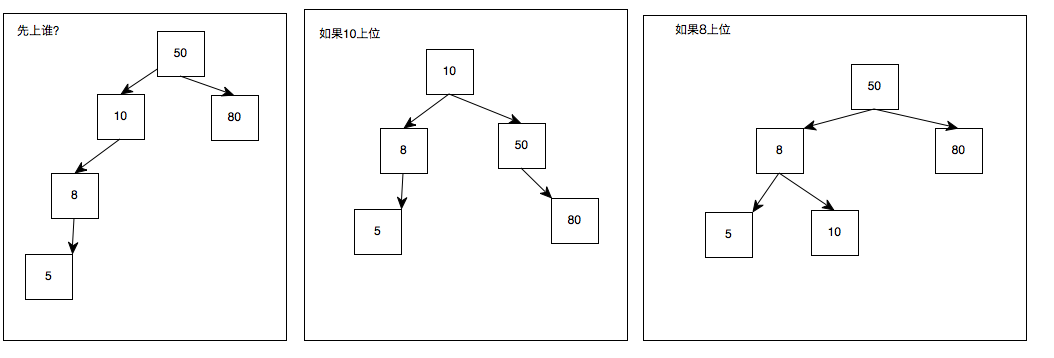
两种都能够保持AVL，但是哪种才是正确的呢

结论是：8上位。

直观理由：1.这样变动更少，2.更安全.3.最近原则

问题来了：没法总是看图，如何用代码表示呢

引用了所谓的平衡因子c

重新看一下LL：

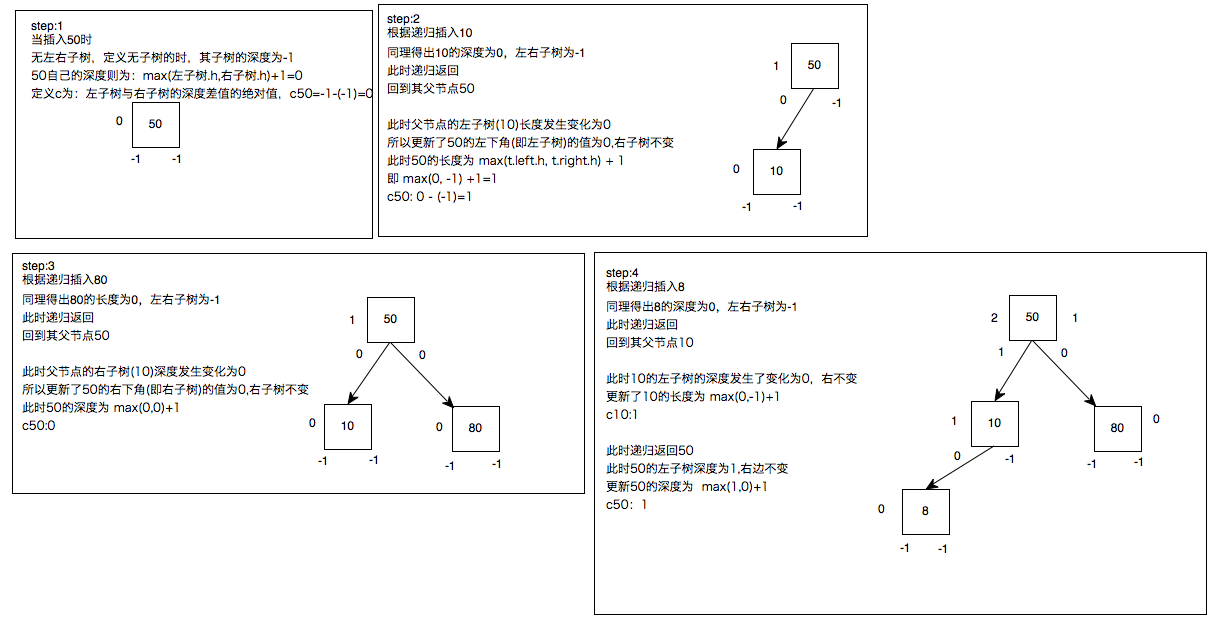
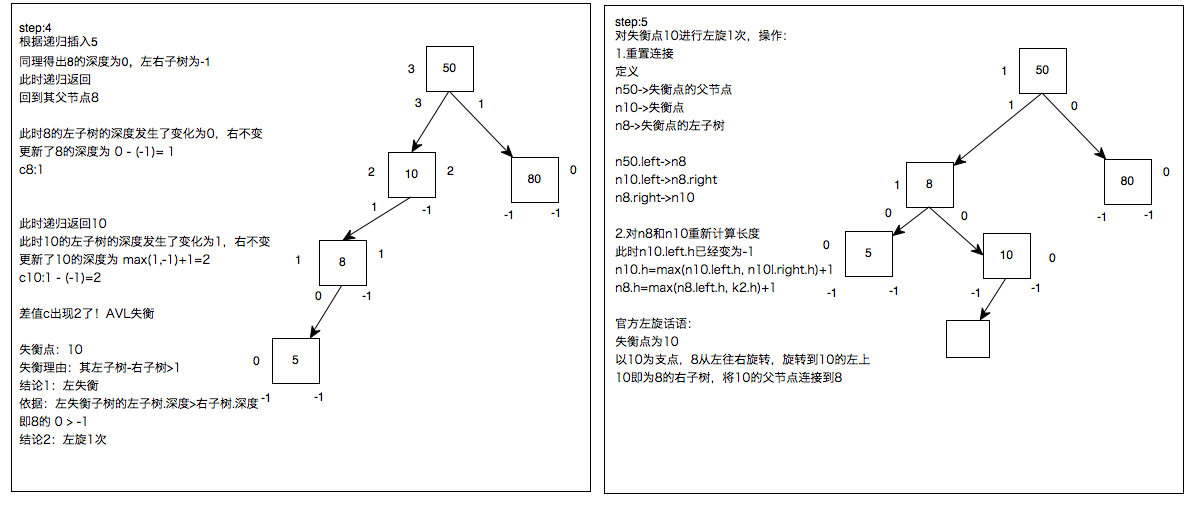
看一下LR

RR RL依据之前没给出深度值的加上深度值就可以了