MT【32】内外圆(Apollonius Circle)的几何证明

另一方面,如果 M 满足(1)式,那么M必然在以PQ为直径的圆上.事实上当M为P或者Q时,这是显然的。当M异于P,Q时,由$\frac{|MB|}{|MC|}=\frac{|PB|}{|PC|}=\lambda,\frac{|MB|}{|MC|}=\frac{|QB|}{|QC|}=\lambda$知MP,MQ分别是$\angle{BMC}$的内角平分线和外交平分线,故$\angle{PMQ}=90^0$,即M在以PQ为直径的圆上。
评:阿式圆因为涉及到内角平分线和外角平分线又称为内外圆,在有些高考题中非常的管用.这个圆的定义大家可以和高中教材中椭圆双曲线的定义做比较,自然会想到以下问题:到两个定点的乘积为定值的点的轨迹是什么?
注:卡西尼卵形线图像:
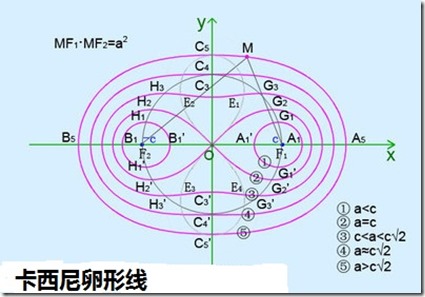
例:
解答:



MT【32】内外圆(Apollonius Circle)的几何证明的更多相关文章
- MT【290】内外圆求三角最值
求$\sqrt{\dfrac{5}{4}-\sin x}+2\sqrt{\dfrac{9}{4}+\cos x-\sin x}$的最小值. 提示:$\sqrt{\dfrac{5}{4}-\sin x} ...
- MT【172】内外圆
$P,Q$是两个定点,M为平面内一个动点,且$\dfrac{|MP|}{|MQ|}=\lambda(\lambda>0,\lambda\ne1)$, 点M的轨迹围成的区域面积为S , 设$S=f ...
- 创建一个圆类Circle的对象,分别设置圆的半径计算并分别显示圆半径、圆面积、圆周长。
编写一个圆类Circle,该类拥有: ①一个成员变量 Radius(私有,浮点型): // 存放圆的半径: ②两个构造方法 Circle( ) // 将半径设为0 Circle(double r ) ...
- 以圆类 Circle 及立体图形类 Solid 为基础设计圆锥类 Cone
学习内容:以圆类 Circle 及立体图形类 Solid 为基础设计圆锥类 Cone 代码示例: import java.util.Scanner; class Point4{ private dou ...
- 以圆类 Circle 及立体图形类 Solid 为基础设计圆柱类 Cylinder
学习内容:以圆类 Circle 及立体图形类 Solid 为基础设计圆柱类 Cylinder 代码示例: import java.util.Scanner;class Point3{ private ...
- 以点类 Point 及平面图形类 Plane 为基础设计圆类 Circle
学习内容:以点类 Point 及平面图形类 Plane 为基础设计圆类 Circle 代码示例: import java.util.Scanner; class Point2{ private dou ...
- 以圆类 Circle 及立体图形类 Solid 为基础设计球类 Sphere
学习内容:以圆类 Circle 及立体图形类 Solid 为基础设计球类 Sphere 代码示例: package 实验三; import java.util.Scanner; class Point ...
- 以圆类 Circle 为基础设计球类 Sphere
学习内容:实验二以圆类 Circle 为基础设计球类 Sphere 代码示例: import java.util.Scanner; class Point{ private double x; pri ...
- 实验二——以点类 Point 为基类设计圆类 Circle
学习内容:以点类 Point 为基类设计圆类 Circle 示例代码: package 实验二; import java.util.Scanner; class Point{//父类Point pri ...
随机推荐
- Jlink使用技巧之烧写SPI Flash存储芯片
前言 大多数玩单片机的人都知道Jlink可以烧写Hex文件,作为ARM仿真调试器,但是知道能烧写SPI Flash的人应该不多,本篇文章将介绍如何使用JLink来烧写或者读取SPI Flash存储器, ...
- asp.net core部署时自定义监听端口,提高部署的灵活性
另一种方式 https://www.cnblogs.com/stulzq/p/9039836.html 代码截图: 贴一下代码,方便复制: //默认端口号5000 string port = &quo ...
- Windows环境下实现Consul服务注册和服务发现
1.首先从官方网站下载Consul,因为我们是使用的Windows系统,所以选择windows版本 https://www.consul.io/downloads.html 2.可以用开发者模式来启动 ...
- RSA公钥文件解密密文的原理分析
前言 最近在学习RSA加解密过程中遇到一个这样的难题:假设已知publickey公钥文件和加密后的密文flag,如何对其密文进行解密,转换成明文~~ 分析 对于rsa算法的公钥与私钥的产生,我们可以了 ...
- C_数据结构_递归实现求阶乘
# include <stdio.h> int main(void) { int val; printf("请输入一个数字:"); printf("val = ...
- Java开发23种设计模式之禅
六大原则 23种设计模式: 总体来说设计模式分为三大类: *创建型模式,共五种:工厂方法模式.抽象工厂模式.单例模式.建造者模式.原型模式. *结构型模式,共七种:适配器模式.装饰器模式.代理模式.外 ...
- B. Vova and Trophies
链接 [https://codeforces.com/contest/1082/problem/B] 题意 给你一个包含GS的字符串,只允许交换一次任意不同位置的字符,问最长的连续G串是多少 分析 很 ...
- Linux期末总结
Linux内核学习总结 1.计算机是如何工作的? 存储程序计算机工作模型 X86汇编基础 汇编一个简单的C程序分析其汇编指令执行过程 2.操作系统是如何工作的? 三个法宝——存储程序计算机.函数调用堆 ...
- Linux内核分析——第五章 系统调用
第五章 系统调用 5.1 与内核通信 1.系统调用在用户空间进程和硬件设备之间添加了一个中间层,该层主要作用有三个: (1)为用户空间提供了一种硬件的抽象接口 (2)系统调用保证了系统的稳定和安全 ( ...
- 软件工程个人项目作业 Individual Project
利用Junit4进行程序模块的测试,回归测试 源码 https://github.com/dpch16303/test/blob/master/%E5%9B%9E%E5%BD%92%E6%B5%8B% ...
