机器学习之 XGBoost和LightGBM

1、基本知识点简介
2、梯度提升树GBDT算法
- 2.1 思路和原理
- 2.2 梯度代替残差建立CART回归树
3、XGBoost提升树算法
4、LightGBM轻量级提升学习方法

1、基本知识点简介

在集成学习的Boosting提升算法中，有两大家族：第一是AdaBoost提升学习方法，另一种是GBDT梯度提升树。
传统的AdaBoost算法：利用前一轮迭代弱学习器的误差来更新训练集的权重，一轮轮迭代下去。
梯度提升树GBDT：也是通过迭代的算法，使用前向分布算法，但是其弱分类器限定了只能使用CART回归树模型。
GBDT算法原理：指通过在残差减小的梯度方向建立boosting tree（提升树），即gradient boosting tree（梯度提升树）。每次建立新模型都是为了使之前模型的残差往梯度方向下降。
XGBoost原理：XGBoost属于集成学习Boosting，是在GBDT的基础上对Boosting算法进行的改进，并加入了模型复杂度的正则项。GBDT是用模型在数据上的负梯度作为残差的近似值，从而拟合残差。XGBoost也是拟合数据残差，并用泰勒展开式（二阶泰勒展开式）对模型损失残差的近似，同时在损失函数上添加了正则化项。
lightGBM，它是微软出的新的boosting框架，基本原理与XGBoost一样，使用基于学习算法的决策树，只是在框架上做了一优化（重点在模型的训练速度的优化）。最主要的是LightGBM使用了基于直方图的决策树算法，基本思想是先把连续的浮点特征值离散化成k个整数，同时构造一个宽度为k的直方图。在遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量，当遍历一次数据后，直方图累积了需要的统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。

2、梯度提升树GBDT算法

2.1 思路和原理

基本思路：假设前一轮迭代得到的强学习器是$f_{t-1}(x)$，损失函数是$L(y, f_{t-1}(x))$，则本轮迭代的目标是找到一个CART回归树模型的弱学习器$h_{t}(x)$，让本轮的损失函数$L(y,f_{t}(x)) = L(y,f_{t-1}(x)) - h_{t}(x)$最小。即本轮迭代找到的损失函数要使样本的损失比上一轮更小。
大牛Freidman提出用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树，第 t 轮的第 i 个样本的损失函数的负梯度表示为：
\[r_{ti} = - [\frac{\partial L(y_{i}, f(x_{i})) }{\partial f(x_{i}) }]_{f(x)=f_{t-1}(x)}\]

2.2 梯度代替残差建立CART回归树

利用$(x_{i}, r_{ti}), (i=1,2,...,m)$（此处损失函数的负梯度代替了一般提升树的残差），我们可以拟合一棵CART回归树，得到第 t 棵回归树，其对应的叶结点区域$R_{tj}, j=1,2,...,J$。其中J为叶子结点的个数。

对于每一个叶子结点的样本，通过使平方误差损失函数最小，输出拟合叶子结点最好的输出值$C_{tj}$（CART回归树中采取的公式是每一个样本的划分单元上的所有实例$x_{i}$的所有输入实例对应的输出平均值，即$\hat{c}_{m} = ave(y_{i} | x_{i} \in R_{m})$），此处输出值为：
\[c_{tj} = arg \min\limits_{c} \sum\limits_{x_{i} \in R_{tj}} L(y_{i}, f_{t-1}(x_{i}) + c)\]
因此本轮决策树的拟合函数为：
\[h_{t}(x) = \sum\limits_{j=1}^{J} c_{tj} I(x \in R_{tj})\]
从而得到本轮的强学习器表达式为：
\[f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J} c_{tj} I(x \in R_{tj})\]
如果是GBDT分类算法，则需要改变损失函数为指数损失函数（类似为AdaBoost算法），或者对数似然损失函数（逻辑回归）。——暂时不作分析。
指数损失函数：$L(y, f(x)) = exp(-Y(f(x)))$
对数损失函数：$L(Y,P(Y|X)) = -log P(Y|X)$

3、XGBoost提升树算法

由于在第 n 棵树训练时，需要用到第n-1棵树的（近似）残差，存在依赖关系，因此GBDT难以实现分布式（也可以实现，但是比较麻烦）。
XGBoost整个过程包括：原始公式表达+泰勒展开式+正则化项的选定+最终目标函数的确定

3.1 XGBoost原理

XGBoost原理：XGBoost属于集成学习Boosting，是在GBDT的基础上对Boosting算法进行的改进，并加入了模型复杂度的正则项。GBDT是用模型在数据上的负梯度作为残差的近似值，从而拟合残差。XGBoost也是拟合数据残差，但其采用泰勒展开式对模型损失残差的近似，同时在损失函数上添加了正则化项。

\[Obj^{t} = \sum_{i=1}^{n} L(y_{i}, \hat{y}_{i}^{(t-1)} + f_{t}(x_{i})) + \Omega (f_{t}) + constant\]

其中$\sum_{i=1}^{n} L(y_{i}, \hat{y}_{i}^{(t-1)})$为损失函数，(t-1)指第(t-1)棵树；$\Omega (f_{t})$为正则项，包括L1、L2；$constant$为常数项。??

3.2 XGBoost中损失函数的泰勒展开

泰勒展开式定义：$f(x+\Delta x) \simeq f(x) + f^{'}(x) \Delta x + \frac{1}{2} f^{''}(x) \Delta x^{2}$

此处$f(x, x+\Delta x)$-----$L(y_{i}, \hat{y}_{i}^{(t-1)} + f_{t}(x_{i}))$，即将$f_{t}(x_{i})$视为$\Delta x$，将$\hat{y}_{i}^{(t-1)} $视为$x$，将$L$函数视为$f$函数。

因此定义一阶导数$g_{i} = \partial_{\hat{y}^{(t-1)}} l(y_{i}, \hat{y}^{(t-1)})$，二阶导数$h_{i} = \partial_{\hat{y}^{(t-1)}}^{2} l(y_{i}, \hat{y}^{(t-1)})$，则有：

\[Obj^{t} = \sum_{i=1}^{n} [l(y_{i}, \hat{y})_{i}^{(t-1)} +g_{i} f_{t}(x_{i}) + \frac{1}{2} h_{i} f_{t}^{2}(x_{i})] + \Omega (f_{t}) + constant\]

$$$$

对于 f 的定义，我们把树拆分成结构部分$q$和叶子权重部分$\omega$。结构函数q把输入映射到叶子的索引号上面去，而$\omega$给定了每个索引号对应的叶子分数是多少？

\[f_{t}(x) = \omega_{q}(x), \omega \in R^{T}, q:R^{d} \to \{1,2,...,T\}\]

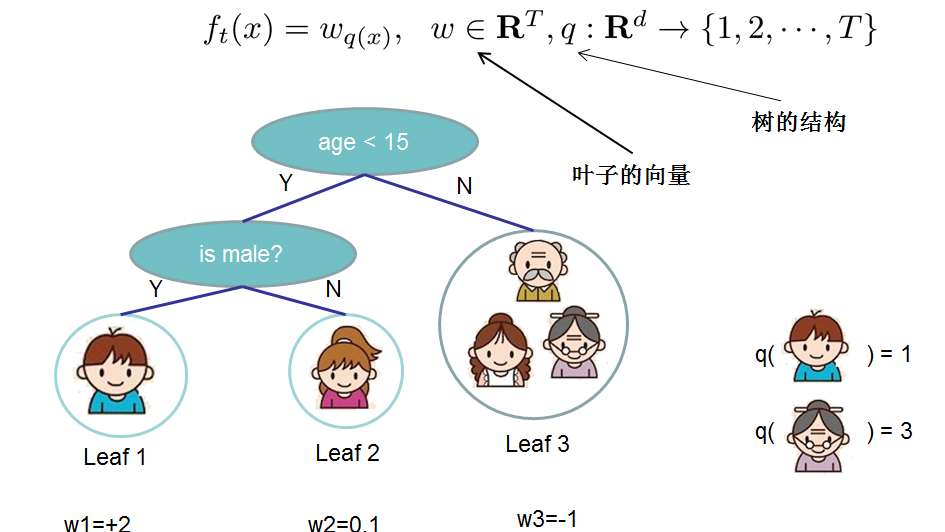
3.3 XGBoost中正则化项的选定

正则化项的选定：定义CART决策树中里面的叶子结点个数为T，每个叶子结点上面输出分数的L2模平方。有：
\[\Omega (f_{t}) = \gamma T + \frac{1}{2}\lambda \sum\limits_{j=1}^{T} \omega_{j}^{2}\]

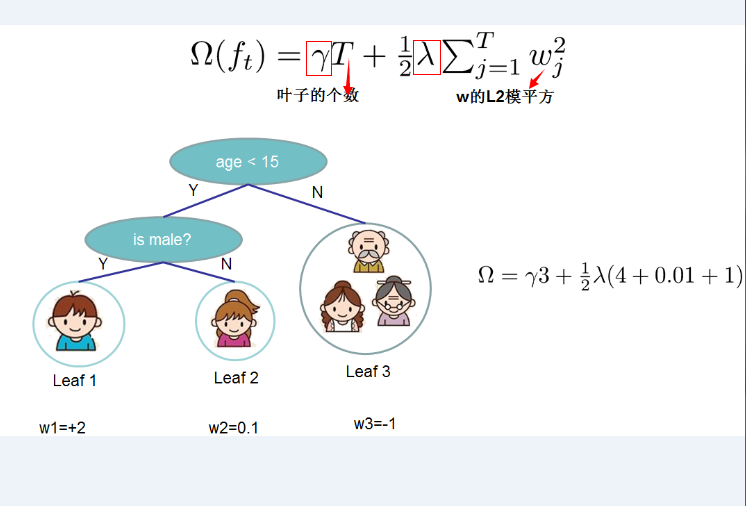
其中$\gamma$和$\lambda$是控制比重参数。定义每个叶子上面样本集合为$I_{j} = {i | q(x_{i}) = j}$，即能个到达这个叶子结点上的所有特征结点，对应权重为$\omega_{j}$，则目标函数（损失函数）变为：
\[Obj^{(t)} \simeq \sum\limits_{i=1}^{n} [g_{i} f_{t}^(x_{i} + \frac{1}{2} h_{i} f_{t}^{2} (x_{i}))] + \Omega(f_{t}) \\ = \sum\limits_{i=1}^{n} [g_{i} \omega_{q}(x_{i}) + \frac{1}{2} h_{i} \omega_{q}^{2}(x_{i})] + \gamma T + \frac{1}{2} \lambda \sum\limits_{j=1}^{T} \omega_{j}^{2} \\ = \sum\limits_{j=1}^{T} [(\sum_{i \in I_{j}} g_{i}) \omega_{j} + \frac{1}{2} (\sum_{i \in I_{j}} h_{i} + \lambda) \omega_{j}^{2}] + \lambda T\]
其中 n 表示第 n 棵树，T表示树中叶子结点个数。

这一目标包含了T个相互独立的单变量二次函数，我们定义：
\[G_{j} = \sum_{i \in I_{j}} g_{i}, i=1,2,...,n; j=1,2,..,T\]
\[H_{j} = \sum_{i \in I_{j}} h_{i}, i=1,2,...,n; j=1,2,..,T\]
这里$G_{j}$为该叶子结点上面样本集合中数据点在误差函数上的一阶导数和二阶导数。

3.4 最终的目标损失函数及其最优解的表达形式

最终公式可以化简为：
\[Obj^{(t)} = \sum\limits_{j=1}^{T} [(\sum_{i \in I_{j}} g_{i}) \omega_{j} + \frac{1}{2} (\sum_{i \in I_{j}} h_{i} + \lambda) \omega_{j}^{2}] + \lambda T \\ = \sum\limits_{j=1}^{T} [G_{j} \omega_{j} + \frac{1}{2} (H_{j} + \lambda) \omega_{j}^{2} + \lambda T]\]
通过令$Obj^{t}$对$\omega_{j}$求导等于0，可以得到
\[\omega_{j}^{*} = - \frac{G_{j}}{H_{j} + \lambda}\]
然后把$\omega_{j}$最优解代入得到：
\[Obj = - \frac{1}{2} \sum\limits_{j=1}^{T} \frac{G_{j}^{2}}{H_{j} + \lambda} + \gamma T\]
结构分数：Obj代表了当我们制定一个树的结构时，目标最多能减少多少，即取最优解，被成为结构分数。
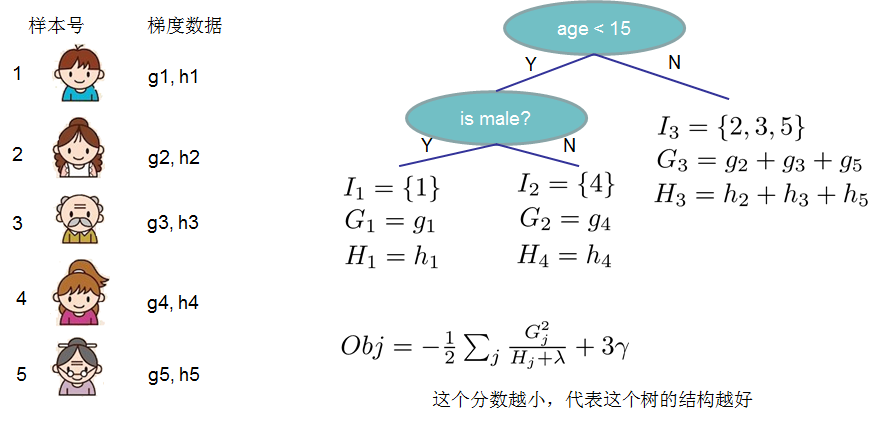
贪心法：指每一次尝试去对已有的叶子加入一个分割。得到的增益为：
\[Gain = \frac{1}{2} [\frac{G_{L}^{2}}{H_{L} + \lambda} + \frac{G_{R}^{2}}{H_{R} + \lambda} - \frac{(G_{L}+G_{R})^{2}}{H_{L} + H_{R} + \lambda}] - \lambda\]

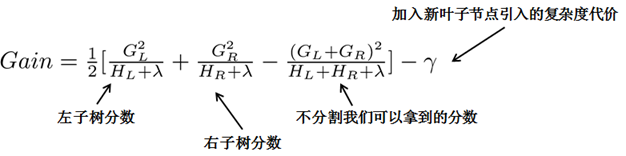
对于每次扩展，我们都需要枚举所有可能的分割方案，例如，通过枚举所有x<a这样的条件，对于某个特定的分割a，我们要计算a左边和右边的导数和。

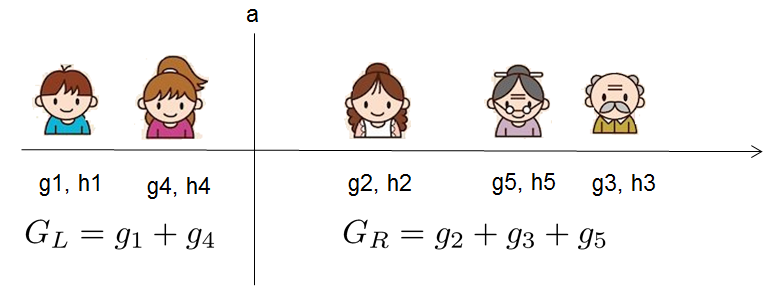
我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和GL和GR，然后用上面的公式计算每个分割方案的分数增益就可以了。

重点：通过引入新叶子的惩罚项$\lambda$，可以优化这个目标函数，对应于决策树的剪枝。当引入的分割带来的增益小于一个阈值的时候，我们就可以剪掉这个分割。（正式推导目标时，计算分数和剪枝这样的策略都能以公式呈现，而不是启发式。）

4、LightGBM轻量级提升学习方法

LightGBM原理和XGBoost类似，通过损失函数的泰勒展开式近似表达残差（包含了一阶和二阶导数信息），另外利用正则化项控制模型的复杂度。但是LightGBM最大的特点是，
1. 通过使用leaf-wise分裂策略代替XGBoost的level-wise分裂策略，通过只选择分裂增益最大的结点进行分裂，避免了某些结点增益较小带来的开销。
2. 另外LightGBM通过使用基于直方图的决策树算法，只保存特征离散化之后的值，代替XGBoost使用exact算法中使用的预排序算法（预排序算法既要保存原始特征的值，也要保存这个值所处的顺序索引），减少了内存的使用，并加速的模型的训练速度。

4.1 leaf-wise分裂策略

（1）XGBoost的level-wise分类策略

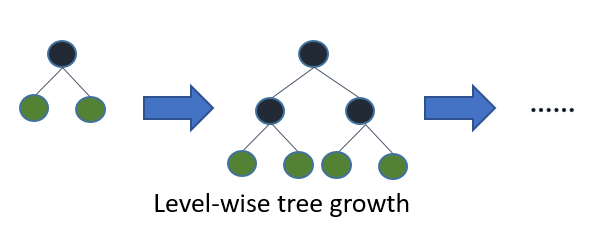
level-wise是指对每一层所有结点做无差别分裂，尽管部分结点的增益比较小，依然会进行分裂，带来了没必要的开销。
（2）LightGBM的leaf-wise分裂策略
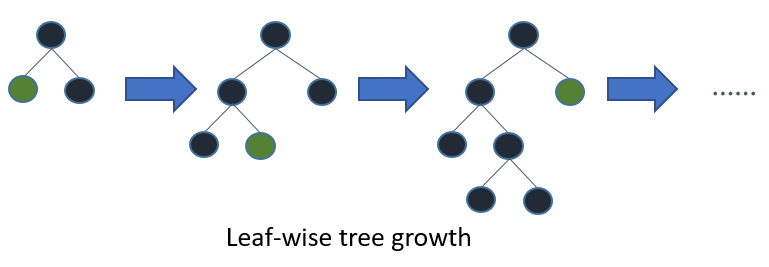
leaf-wise是指在当前所有叶子结点中选择分类增益最大的结点进行分裂，并进行最大深度限制，避免过拟合。
二叉树的分裂增益公式为：

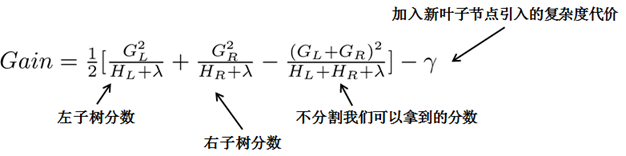
其中$\frac{1}{2} [\frac{G_{L}^{2}}{H_{L} + \lambda} + \frac{G_{R}^{2}}{H_{R} + \lambda} - \frac{(G_{L}+G_{R})^{2}}{H_{L} + H_{R} + \lambda}]$是指不考虑其他因素，通过分裂得到的增益，但实际上每次引入新叶子结点，都会带来复杂度的代价，即$\gamma$。
$G_{j} = \sum_{i \in I_{j}} g_{i}, i=1,2,...,n; j=1,2,..,T$，$H_{j} = \sum_{i \in I_{j}} h_{i}, i=1,2,...,n; j=1,2,..,T$
这里$G_{j}$为该叶子结点上面样本集合中数据点在误差函数上的一阶导数和二阶导数。

4.2 基于直方图的排序算法

直方图算法基本实现：是指先把连续的浮点特征值离散化成 k 个整数，同时构造一个宽度为 k 的直方图。在遍历数据的时候，根据离散化后的值作为是索引，在直方图中累积统计量，然后根据直方图的离散值，遍历寻找最优的分割点。在XGBoost中需要遍历所有离散化的值，而LightGBM通过建立直方图只需要遍历 k 个直方图的值。
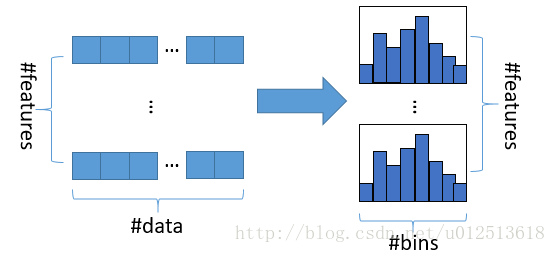
使用直方图的优点：
- 明显减少内存的使用，因为直方图不需要额外存储预排序的结果，而且可以只保存特征离散化后的值。
- 遍历特征值时，不需要像XGBoost一样需要计算每次分裂的增益，而是对每个特征只需要计算建立直方图的个数，即k次，时间复杂度由O(#data * #feature)优化到O(k * #feature)。（由于决策树本身是弱分类器，分割点是否精确并不是太重要，因此直方图算法离散化的分割点对最终的精度影响并不大。另外直方图由于取的是较粗略的分割点，因此不至于过度拟合，起到了正则化的效果）
- LightGBM的直方图能做差加速。一个叶子的直方图可以由它的父亲结点的直方图与它兄弟的直方图做差得到。构造的直方图本来需要遍历该叶子结点上所有数据，但是直方图做差仅需遍历直方图的k个桶即可（即直方图区间），速度上可以提升一倍。如下图：

4.3 支持类别特征和高效并行处理

直接支持类别特征，不需要做one-hot编码。大多数机器学习都无法直接支持类别特征，一般需要把类别进行特征编码，这样就降低了空间和时间的效率。但是LightGBM可以在对离散特征分裂时，每个取值都当作一个桶，分裂时的增益为“是否属于某个类别category”的gain。
支持高效并行：包括特征并行和数据并行。（减少的是分割数据的时间，而不是模型训练的时间）
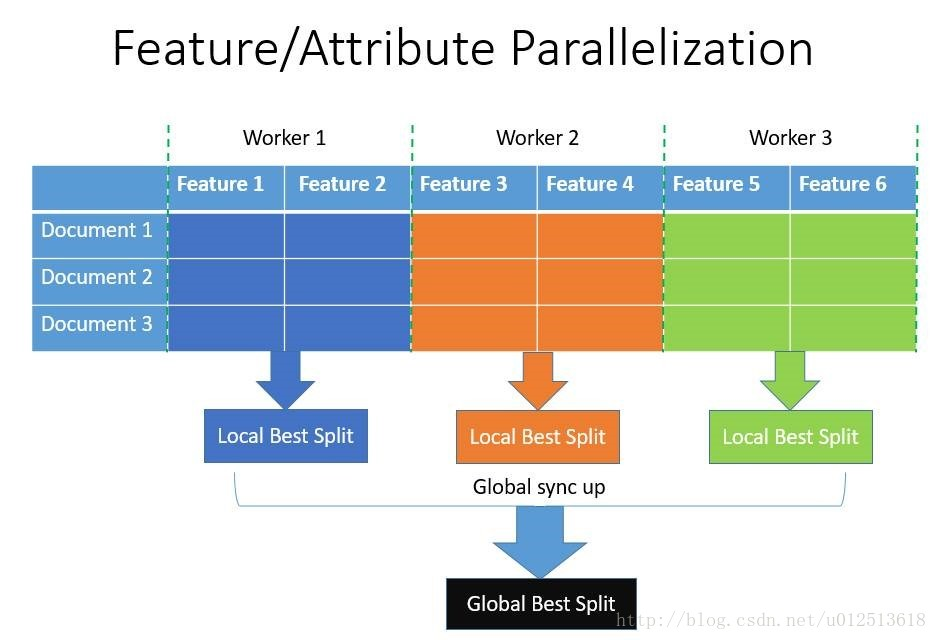
- 特征并行：即在不同机器上在不同的特征集上分别寻找最优的分割点，然后在机器间同步最优的分割点。其通过本地保存全部数据避免对数据切分结果的通信。
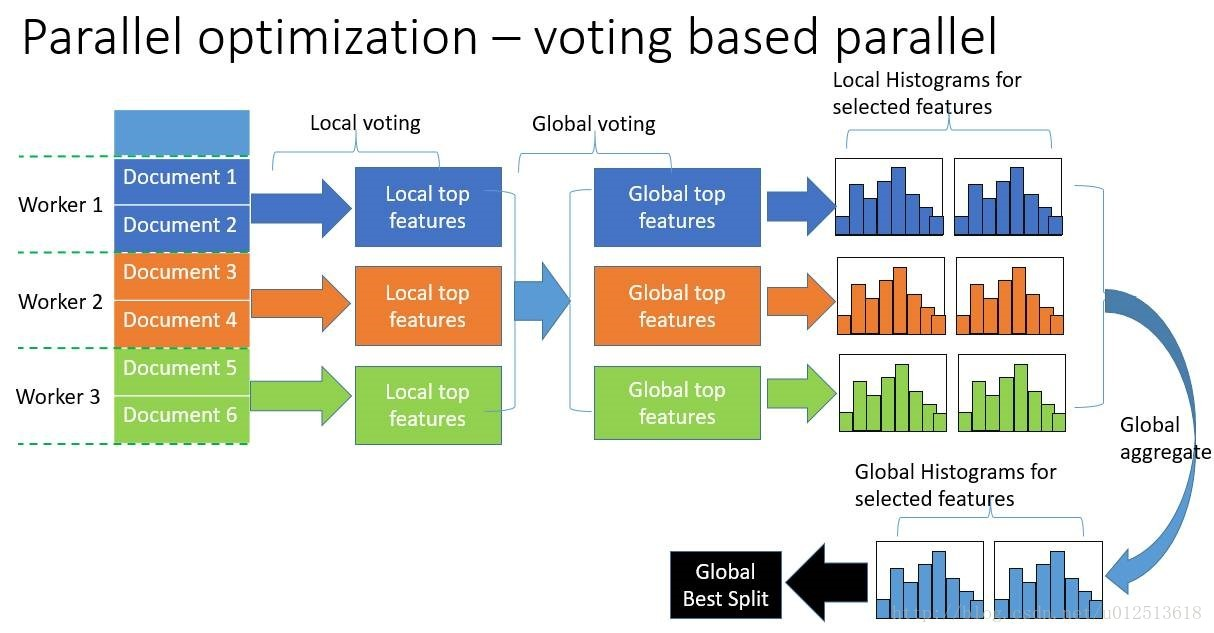
- 数据并行：即让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。其使用分散规约（Reduce scatter）把直方图合并的任务分摊到不同的机器上，降低了通信量，并利用直方图做差，减少了通信量，即减少了通信时间。

参考：
1、GBDT：https://www.cnblogs.com/pinard/p/6140514.html
2、XGBoost：https://www.cnblogs.com/zhouxiaohui888/p/6008368.html
3、LightGBM官方文档：https://lightgbm.readthedocs.io/en/latest/Features.html
4、LightGBM图形理解：https://www.cnblogs.com/jiangxinyang/p/9337094.html