二叉搜索树（Binary Search Tree）

二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树。

二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

• 非空左子树的所有键值小于其根结点的键值；
• 非空右子树的所有键值大于其根结点的键值；
• 左右子树都是二叉搜索树；

Wiki中的定义：

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• The left and right subtrees each must also be a binary search tree.
• Each node can have up to two successor nodes.
• There must be no duplicate nodes.
• A unique path exists from the root to every other node.

二叉搜索树操作的特别函数：

Position Find（ElementType X，BinTree BST）：从二叉搜索树BST查找元素X，返回其所在结点的地址；

Position FindMin（BinTree BST）：从二叉搜索树BST中查找并返回最小元素所在结点的地址；

Position FindMax（BinTree BST）：从二叉搜索树BST中查找并返回最大元素所在结点的地址；

BinTree Insert（ElementType X，BinTree BST）：把元素X结点插入到二叉搜索树BST中；

BinTree Delete（ElementType X，BinTree BST）：从二叉搜索树BST中删除元素X结点；

---

【二叉搜索树的查找操作：Find】

1、查找从根结点开始，如果树为空，返回NULL；

2、若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：

• 如果X小于根结点的键值，只需在左子树中继续搜索；
• 如果X大于根结点的键值，只需在右子树中继续搜索；
• 若两者比较结果是相等，搜索完成，返回指向此结点的指针；

递归查找操作：

 Position BST_Find(ElementType X, BinTree BST)
 {
     if(BST == NULL)
         return NULL;

     if(X > BST->Data)
         return BST_Find(X, BST->Right);
     else if(X < BST->Data)
         return BST_Find(X, BST->Left);
     else
         return BST;
 }

非递归查找操作：

 Postion BST_Find_ext(ElementType X, BinTree BST)
 {
     while(BST != NULL)
     {
         if(X > BST->Data)
             BST = BST->Right;
         else if(X < BST->Data)
             BST = BST->Left;
         else
             return BST;
     }
     return NULL;
 }

【二叉搜索树查找最大元素FindMax和最小元素FindMin】

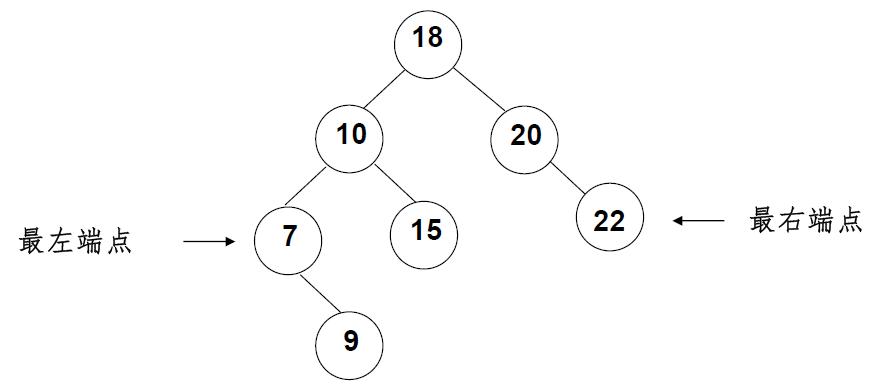
最大元素一定是在树的最右分支的端结点上；

最小元素一定是在树的最左分支的端结点上；

递归查找Min和Max：

 Position BST_FindMin(BinTree BST)
 {
     if(BST == NULL)
         return NULL;
     else if(BST->Left == NULL)
         return BST;
     else
         return BST_FindMin(BST->Left);
 }

 Position BST_FindMax(BinTree BST)
 {
     if(BST == NULL)
         return NULL;
     else if(BST->Right == NULL)
         return BST;
     else
         return BST_FindMax(BST->Right);
 }

非递归查找Min和Max：

 Position BST_FindMin_ext(BinTree BST)
 {
     if(BST != NULL)
     {
         while(BST->Left != NULL)
             BST = BST->Left;
     }
     return BST;
 }

 Position BST_FindMax_ext(BinTree BST)
 {
     if(BST != NULL)
     {
         while(BST->Right != NULL)
             BST = BST->Right;
     }
     return BST;
 }

【二叉搜索树的插入操作：Insert】

 BinTree BST_Insert(ElementType X, BinTree BST)
 {
     if(BST == NULL)
     {
         // 若原树为空,生成并返回一个结点的二叉搜索树
         BST = malloc(sizeof(struct TreeNode));
         BST->Data  = X;
         BST->Left  = NULL;
         BST->Right = NULL;
     }
     else
     {
         // 开始找要插入元素的位置
         if(X < BST->Data)
             BST->Left = BST_Insert(X, BST->Left); // 递归插入左子树
         else if(X > BST->Data)
             BST->Right = BST_Insert(X, BST->Right); // 递归插入右子树
         // else X已经存在,什么都不做
     }
     return BST;
 }

【二叉搜索树的删除操作：Delete】

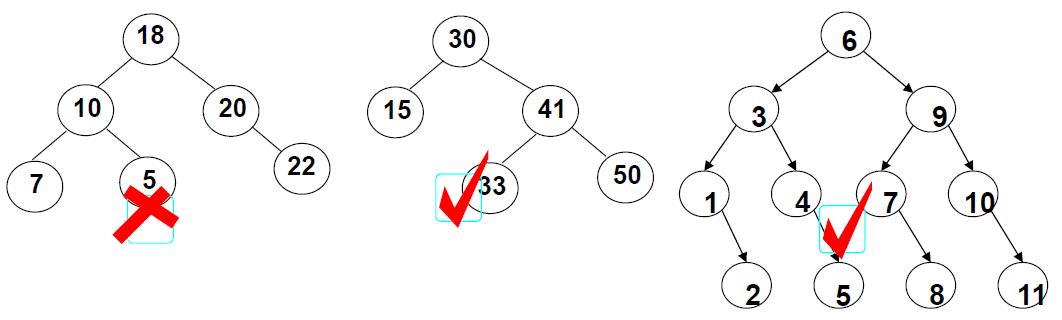
二叉搜索树的删除操作需要考虑三种情况：

• 要删除的是叶结点：直接删除，并修改其父结点指针置为NULL；
• 要删除的结点只有一个孩子结点：将其父结点的指针指向要删除结点的孩子结点；
• 要删除的结点有左右两棵子树：用另一个结点替代被删除结点，右子树的最小元素 或者 左子树的最大元素；

 BinTree BST_Delete(ElementType X, BinTree BST)
 {
     Position Tmp;

     if(BST == NULL)
     {
         printf("warning: xxx\n"); // 未找到要删除的元素
     }
     else if(X < BST->Data)
     {
         BST->Left = BST_Delete(X, BST->Left); // 左子树递归删除
     }
     else if(X > BST->Data)
     {
         BST->Right = BST_Delete(X, BST->Right); // 右子树递归删除
     }
     else
     {
         // 被删除结点有左右两个子结点
         if(BST->Left != NULL && BST->Right != NULL)
         {
             // 在右子树中找到最小的元素填充删除结点
             Tmp = BST_FindMin(BST->Right);
             BST->Data = Tmp->Data;
             // 在删除结点的右子树中删除最小元素
             BST->Right = BST_Delete(BST->Data, BST->Right);
         }
         else // 被删除结点有一个或无子结点
         {
             Tmp = BST;
             if(BST->Left == NULL) // 有右孩子或者无子结点
                 BST = BST->Right;
             else if(BST->Right == NULL) // 有左孩子或者无子结点
                 BST = BST->Left;
             free(Tmp);
         }
     }
     return BST;
 }

---

Wiki链接：

Binary_search_tree ：http://en.wikipedia.org/wiki/Binary_search_tree