洛谷P1930 亚瑟王的宫殿 Camelot

P1930 亚瑟王的宫殿 Camelot

• • 19通过
  • 53提交
• 题目提供者JOHNKRAM
• 标签USACO
• 难度提高+/省选-

提交  讨论  题解

最新讨论

• 暂时没有讨论

题目描述

很久以前，亚瑟王和他的骑士习惯每年元旦去庆祝他们的友谊。为了纪念上述事件， 我们把这些故事看作是一个棋盘游戏。有一个国王和若干个骑士被放置在一个由许多方格 组成的棋盘上，没有两个骑士在同一个方格内。

这个例子是标准的 8*8 棋盘

国王可以移动到任何一个相邻的方格，从下图中黑子位置到下图中白子位置前提是他 不掉出棋盘之外。

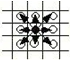
一个骑士可以从下图中黑子位置移动到下图中白子位置(走“日”字形） 但前提是他 不掉出棋盘之外。

在游戏中，玩家可在每个方格上放不止一个棋子，假定方格足够大，任何棋子都不会 阻碍到其他棋子正常行动。

玩家的任务就是把所有的棋子移动到同一个方格里——用最小的步数。为了完成这个 任务，他必须按照上面所说的规则去移动棋子。另外，玩家可以选择一个骑士跟国王从他 们两个相遇的那个点开始一起行动，这时他们按照骑士的行动规则行动，其他的单独骑士 则自己一直走到集中点。骑士和国王一起走的时候，只算一个人走的步数。

请计算他们集中在一起的最小步数，而且玩家必须自己找出这个集中点。当然，这些 棋子可以在棋盘的任何地方集合。

输入输出格式

输入格式：

第一行： 两个用空格隔开的整数：R,C 分别为棋盘行和列的长。不超过 26 列，40 行。

第二行到结尾： 输入文件包含了一些有空格隔开的字母/数字对，一行有一个或以 上。第一对为国王的位置，接下来是骑士的位置。可能没有骑士，也可能整个棋盘都是骑 士。行从 1 开始，列从大写字母 A 开始。

输出格式：

单独一行表示棋子集中在一个方格的最小步数。

输入输出样例

输入样例#1：

8  8
D  4
A  3  A  8
H  1  H  8

输出样例#1：

10

说明

【样例说明】

他们集中在 B5。

骑士 1: A3 - B5 (1 步)

骑士 2: A8 - C7 - B5 (2 步)

骑士 3: H1 - G3 - F5 - D4 (此时国王开始与这个骑士一起走) - B5 (4 步) 骑士 4: H8 - F7 - D6 - B5 (3 步)

1 + 2 + 4 + 3 = 10 步

题目翻译来自NOCOW。

USACO Training Section 3.3

分析：这道题是一道很明显的搜索题，因为集合点没告诉，所以要枚举集合点，这样的话涉及到多次计算，先进行预处理，处理每两个点之间距离，因为是无权无向图，用bfs就可以了，如果不考虑骑士背国王的话，只需要把所有骑士的点到集合点的距离加起来并加上国王与集合点的横纵坐标的差的最大值即可(国王可以八个方向走)，如果考虑背国王的话，有点麻烦.首先你不知道是哪个骑士背国王，然后不知道在哪背，因为国王也要走动，这样的话枚举背的骑士和背的地点，根据之前预处理好的数组计算即可.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>

using namespace std;

int r, c, dis[][][][],num,ans = ;

const int dr[] = { -,-,,,,,-,- };
const int dc[] = { ,,,,-,-,-,- };

struct node
{
    int r, c;
}king,qishi[];

bool vis[][];

bool check(int x, int y)
{
    if (x >=  && x <= r && y >=  && y <= c)
        return true;
    return false;
}

void bfs(int x,int y) {
    int r, c, step;
    queue<node> q;
    node temp;
    temp.r = x;
    temp.c = y;
    q.push(temp);
    memset(vis, false, sizeof(vis));
    dis[x][y][x][y] = ;
    vis[x][y] = true;

    while (!q.empty()) {
        node u = q.front();
        q.pop();
        step = dis[x][y][u.r][u.c];
        for (int i = ;i<;++i) {
            int r = u.r + dr[i];
            int c = u.c + dc[i];
            if (check(r, c) && !vis[r][c]) {
                vis[r][c] = true;
                dis[x][y][r][c] = step + ;
                node temp;
                temp.r = r;
                temp.c = c;
                q.push(temp);
            }
        }
    }
}

int main()
{
    scanf("%d%d", &r, &c);
    char s[];
    int t;
    scanf("%s %d", s, &t);
    king.r = t;
    king.c = s[] - 'A' + ;
    while (scanf("%s%d", s, &t) == )
    {
        qishi[++num].r = t;
        qishi[num].c = s[] - 'A' + ;
    }
    for (int i = ; i <= r; i++)
        for (int j = ; j <= c; j++)
            for (int k = ; k <= r; k++)
                for (int l = ; l <= c; l++)
                    dis[i][j][k][l] = ;
    for (int i = ; i <= r; i++)
        for (int j = ; j <= c; j++)
            bfs(i, j);
    for (int i = ; i <= r; i++)
        for (int j = ; j <= c; j++)
        {
            int temp = ;
            for (int k = ; k <= num; k++)
                temp += dis[qishi[k].r][qishi[k].c][i][j];
            ans = min(ans, temp + max(abs(king.r - i), abs(king.c - j)));
            for (int k = ; k <= num; k++)
            {
                int dx = qishi[k].r, dy = qishi[k].c;
                int t = temp - dis[dx][dy][i][j];
                if (t >= ans) //最优性剪枝
                    continue;
                for (int l = ; l <= r; l++)
                    for (int s = ; s <= c; s++)
                        ans = min(ans, t + dis[l][s][dx][dy] + dis[l][s][i][j] + max(abs(king.r - l), abs(king.c - s)));
            }
        }
    printf("%d\n", ans);

    return ;
}