(六) 6.3 Neurons Networks Gradient Checking
BP算法很难调试,一般情况下会隐隐存在一些小问题,比如(off-by-one error),即只有部分层的权重得到训练,或者忘记计算bais unit,这虽然会得到一个正确的结果,但效果差于准确BP得到的结果。
有了cost function,目标是求出一组参数W,b,这里以 表示,cost function 暂且记做
表示,cost function 暂且记做 。假设
。假设 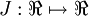 ,则
,则 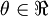 ,即一维情况下的Gradient Descent:
,即一维情况下的Gradient Descent:
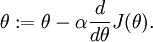
根据6.2中对单个参数单个样本的求导公式:
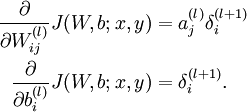
可以得到每个参数的偏导数,对所有样本累计求和,可以得到所有训练数据对参数  的偏导数记做
的偏导数记做 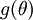 ,
,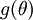 是靠BP算法求得的,为了验证其正确性,看下图回忆导数公式:
是靠BP算法求得的,为了验证其正确性,看下图回忆导数公式:
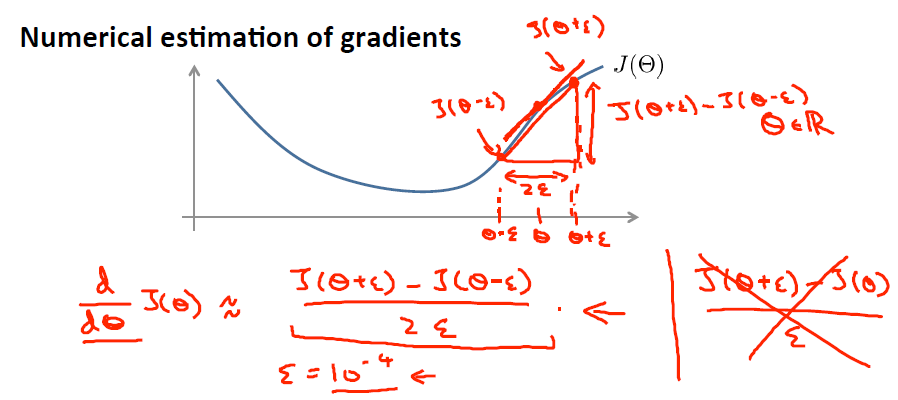
可见有: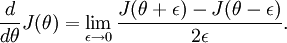 那么对于任意
那么对于任意  值,我们都可以对等式左边的导数用:
值,我们都可以对等式左边的导数用:
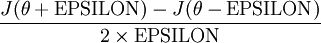 来近似。
来近似。
给定一个被认为能计算 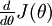 的函数
的函数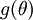 ,可以用下面的数值检验公式
,可以用下面的数值检验公式
应用时,通常把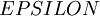 设置为一个很小的常量,比如在
设置为一个很小的常量,比如在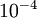 数量级,最好不要太小了,会造成数值的舍入误差。上式两端值的接近程度取决于
数量级,最好不要太小了,会造成数值的舍入误差。上式两端值的接近程度取决于 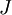 的具体形式。假定
的具体形式。假定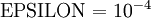 的情况下,上式左右两端至少有4位有效数字是一样的(通常会更多)。
的情况下,上式左右两端至少有4位有效数字是一样的(通常会更多)。
当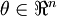 是一个n维向量而不是实数时,且
是一个n维向量而不是实数时,且 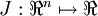 ,在 Neorons Network 中,J(W,b)可以想象为 W,b 组合扩展而成的一个长向量
,在 Neorons Network 中,J(W,b)可以想象为 W,b 组合扩展而成的一个长向量  ,现在又一个计算
,现在又一个计算 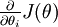 的函数
的函数 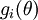 ,如何检验
,如何检验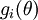 能否输出到正确结果呢,用
能否输出到正确结果呢,用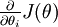 的取值来检验,对于向量的偏导数:
的取值来检验,对于向量的偏导数:

根据上图,对  i 求导时,只需要在向量的第i维上进行加减操作,然后求值即可,定义
i 求导时,只需要在向量的第i维上进行加减操作,然后求值即可,定义 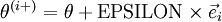 ,其中
,其中
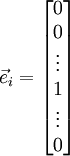
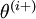 和
和  几乎相同,除了第
几乎相同,除了第  行元素增加了
行元素增加了 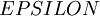 ,类似地,
,类似地,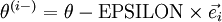 得到的第
得到的第  行减小了
行减小了 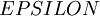 ,然后求导并与
,然后求导并与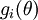 比较:
比较:
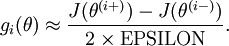
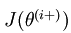 中的参数对应的是参数向量中一个分量的细微变化,损失函数J 在不同情况下会有不同的值(比如三层NN 或者 三层autoencoder(需加上稀疏项)),上式中左边为BP算法的结果,右边为真正的梯度,只要两者很接近,说明BP算法是在正确工作,对于梯度下降中的参数是按照如下方式进行更新的:
中的参数对应的是参数向量中一个分量的细微变化,损失函数J 在不同情况下会有不同的值(比如三层NN 或者 三层autoencoder(需加上稀疏项)),上式中左边为BP算法的结果,右边为真正的梯度,只要两者很接近,说明BP算法是在正确工作,对于梯度下降中的参数是按照如下方式进行更新的:
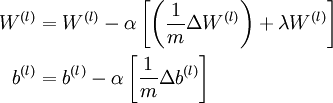
即有 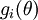 分别为:
分别为:
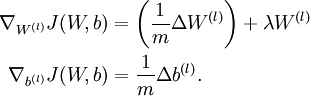
最后只需总体损失函数J(W,b)的偏导数与上述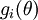 的值比较即可。
的值比较即可。
除了梯度下降外,其他的常见的优化算法:1) 自适应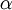 的步长,2) BFGS L-BFGS,3) SGD,4) 共轭梯度算法,以后涉及到再看。
的步长,2) BFGS L-BFGS,3) SGD,4) 共轭梯度算法,以后涉及到再看。
(六) 6.3 Neurons Networks Gradient Checking的更多相关文章
- CS229 6.3 Neurons Networks Gradient Checking
BP算法很难调试,一般情况下会隐隐存在一些小问题,比如(off-by-one error),即只有部分层的权重得到训练,或者忘记计算bais unit,这虽然会得到一个正确的结果,但效果差于准确BP得 ...
- (六) 6.1 Neurons Networks Representation
面对复杂的非线性可分的样本是,使用浅层分类器如Logistic等需要对样本进行复杂的映射,使得样本在映射后的空间是线性可分的,但在原始空间,分类边界可能是复杂的曲线.比如下图的样本只是在2维情形下的示 ...
- (六) 6.2 Neurons Networks Backpropagation Algorithm
今天得主题是BP算法.大规模的神经网络可以使用batch gradient descent算法求解,也可以使用 stochastic gradient descent 算法,求解的关键问题在于求得每层 ...
- (六)6.10 Neurons Networks implements of softmax regression
softmax可以看做只有输入和输出的Neurons Networks,如下图: 其参数数量为k*(n+1) ,但在本实现中没有加入截距项,所以参数为k*n的矩阵. 对损失函数J(θ)的形式有: 算法 ...
- (六)6.5 Neurons Networks Implements of Sparse Autoencoder
一大波matlab代码正在靠近.- -! sparse autoencoder的一个实例练习,这个例子所要实现的内容大概如下:从给定的很多张自然图片中截取出大小为8*8的小patches图片共1000 ...
- (六)6.16 Neurons Networks linear decoders and its implements
Sparse AutoEncoder是一个三层结构的网络,分别为输入输出与隐层,前边自编码器的描述可知,神经网络中的神经元都采用相同的激励函数,Linear Decoders 修改了自编码器的定义,对 ...
- (六)6.13 Neurons Networks Implements of stack autoencoder
对于加深网络层数带来的问题,(gradient diffuse 局部最优等)可以使用逐层预训练(pre-training)的方法来避免 Stack-Autoencoder是一种逐层贪婪(Greedy ...
- Coursera Deep Learning 2 Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization - week1, Assignment(Gradient Checking)
声明:所有内容来自coursera,作为个人学习笔记记录在这里. Gradient Checking Welcome to the final assignment for this week! In ...
- 课程二(Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization),第一周(Practical aspects of Deep Learning) —— 4.Programming assignments:Gradient Checking
Gradient Checking Welcome to this week's third programming assignment! You will be implementing grad ...
随机推荐
- proxool
配置database.xml <!--数据源 读写 --> <bean id="dataSourceRW" class="com.elong.ihote ...
- PHP使用SOAP调用.net的WebService数据
需要和一个.net系统进行数据交换,对方提供了一个WebService接口,使用PHP如何调用这个数据呢,下面就看看使用SOAP调用的方法吧 这个与一般的PHP POST或GET传值再查库拿数据的思路 ...
- ExtJs布局之table
<!DOCTYPE html> <html> <head> <title>ExtJs</title> <meta http-equiv ...
- BZOJ 1046: [HAOI2007]上升序列 LIS -dp
1046: [HAOI2007]上升序列 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 3438 Solved: 1171[Submit][Stat ...
- CentOS目录树详细解释
[sdm_download id=”292″ fancy=”1″] /boot 该目录默认下存放的是Linux的启动文件和内核. initramfs-* 系统启动时的模块供应的主要来源 启动系统所需加 ...
- java string,需要进行首字母大写改写
java string,需要进行首字母大写改写,网上大家的思路基本一致,就是将首字母截取,转化成大写然后再串上后面的,类似如下代码 //首字母大写 public static String c ...
- k近邻法
k近邻法(k nearest neighbor algorithm,k-NN)是机器学习中最基本的分类算法,在训练数据集中找到k个最近邻的实例,类别由这k个近邻中占最多的实例的类别来决定,当k=1时, ...
- Jquery正则表达式公式.例子
1.非负整数 /^\d+$/ 2.正整数 /^[0-9]*[1-9][0-9]*$/ 3.非正整数 /^((-\d+)|(0+))$/ ...
- java 无法找到main类解决办法
java 无法找到main类解决办法 如果Java类有包名,你必须建相应的包文件夹并把文件编译或拷贝到到相应的文件夹下: 如下: 1.源文件文件: E:\test\src\tes ...
- 测试 float
关于blog上对 float的许多讨论,这个函数不对,那个运算出错. 其实原因不在这里,根源是计算机没有向你保证你看到的就是真实的,都是一厢情愿而已. 废话不说.下面是测试,一看就明白.再不明白的看看 ...