洛谷——P1265 公路修建

P1265 公路修建

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式

输入格式：

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

输出格式：

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

输入输出样例

输入样例#1：

4
0 0
1 2
-1 2
0 4

输出样例#1：

6.47

说明

修建的公路如图所示：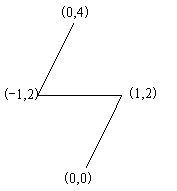

prim求最小生成树

#include<cmath>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 5100
#define maxn 9999999
using namespace std;
double s[N],l[N];
int n,m,fa[N*N];
long long x,y,t,sum,fx,fy,xx[N*N],yy[N*N];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int x,y;
    double z;
}edge[N<<];
int cmp(Edge a,Edge b)
{
    return a.z<b.z;
}
int find(int x)
{
    if(fa[x]==x) return x;
    fa[x]=find(fa[x]);
    return fa[x];
}
int prim(int x)
{
    ;
    ;i<=n;i++)
    {
        s[i]=x;
        l[i]=sqrt((xx[x]-xx[i])*(xx[x]-xx[i])+(yy[x]-yy[i])*(yy[x]-yy[i]));
    }
    s[x]=-;
    ;i<=n;i++)
    {
        t=-;sum=maxn;
        ;j<=n;j++)
         &&sum>l[j])
         {
             sum=l[j];
             t=j;
         }
        )
        {
            s[t]=-;ans+=l[t];
            ;j<=n;j++)
            {
                double ss=sqrt((xx[t]-xx[j])*(xx[t]-xx[j])+(yy[t]-yy[j])*(yy[t]-yy[j]));
                &&ss<l[j])
                {
                    l[j]=ss;
                    s[j]=t;
                }
            }
        }
    }
    printf("%.2lf",ans);
}
int main()
{
    n=read();
    ;i<=n;i++)
     xx[i]=read(),yy[i]=read();
    prim();
    ;
}