UVA 11346 Probability

题目描述

PDF

输入输出格式

输入格式：

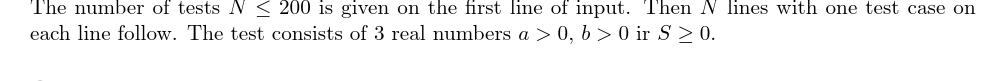
输出格式：

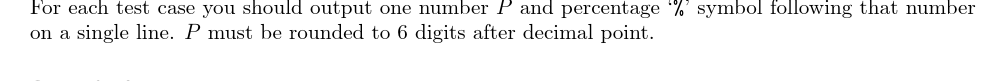
输入输出样例

输入样例#1：

3
10 5 20
1 1 1
2 2 0

输出样例#1：

23.348371%
0.000000%
100.000000%

发现求的是一个和 反比例函数有关的积分，吓得我赶紧去学习了一波积分(之前一直不会还这么淡定2333)。
积分就是导数的反运算嘛，然后 ln(x)的导数是 1/x 所以反比例函数的积分就是 ln(),然后直接做就行了2333

#include<bits/stdc++.h>
#define ll long long
using namespace std;
#define D double
const D eps=1e-12;
D A,B,S,ANS,X;
int T;

inline void solve(){
	ANS=0,scanf("%lf%lf%lf",&A,&B,&S);
	if(A*B<=S) puts("0.000000%");
	else if(S<=eps) puts("100.000000%");
	else{
		X=S/B,ANS=(A-X)*B;
		ANS-=S*(log(A)-log(X));
		printf("%.6lf%\n",ANS/(A*B)*100);
	}
}

int main(){
	scanf("%d",&T);
	while(T--) solve();
	return 0;
}