Cards BZOJ 1004

Cards

【问题描述】

　　小春现在很清闲,面对书桌上的N张牌,他决定给每张染色,目前小春只有3种颜色:红色,蓝色,绿色.他询问Sun有多少种染色方案,Sun很快就给出了答案.进一步,小春要求染出Sr张红色,Sb张蓝色,Sg张绝色.他又询问有多少种方案,Sun想了一下,又给出了正确答案. 最后小春发明了M种不同的洗牌法,这里他又问Sun有多少种不同的染色方案.两种染色方法相同当且仅当其中一种可以通过任意的洗牌法(即可以使用多种洗牌法,而每种方法可以使用多次)洗成另一种.Sun发现这个问题有点难度,决定交给你,答案可能很大,只要求出答案除以P的余数(P为质数).

【输入格式】

　　第一行输入 5 个整数：Sr,Sb,Sg,m,p(m<=60,m+1<p<100)。n=Sr+Sb+Sg。接下来 m 行，每行描述一种洗牌法，每行有 n 个用空格隔开的整数 X1X2...Xn，恰为 1 到 n 的一个排列，表示使用这种洗牌法，第 i位变为原来的 Xi位的牌。输入数据保证任意多次洗牌都可用这 m种洗牌法中的一种代替，且对每种洗牌法，都存在一种洗牌法使得能回到原状态。

【输出格式】

不同染法除以P的余数

【样例输入】

1 1 1 2 7
2 3 1
3 1 2

【样例输出】

2

【样例解释】

有2种本质上不同的染色法RGB和RBG，使用洗牌法231一次可得GBR 和BGR，使用洗牌法312一次可得BRG和GRB。

【数据范围】

100%数据满足：Max{Sr,Sb,Sg}<=20。

---

题解：

Burnside引理：用D(a_i)表示在置换a_i下不变的元素个数。L表示本质不同的方案数。G表示置换群。|G|表示置换群的大小。

置换群简单地讲就是给定置换，所有置换的置换所组成的集合就是置换群

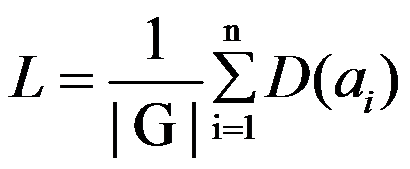
举个例子：

4个置换组成的置换群：

1 2 3 4

2 3 4 1

3 4 1 2

4 1 2 3

假设我们有2种颜色用0与1表示

第一种：所有方案都不变，D(a₁) = 16

第二种：0000、1111，D(a₂) = 2

第三种：0000、1111、0101、1010，D(a3) = 4

第四种：0000、1111，D(a₄) = 2

那么 L = (16 + 2 + 4 + 2) / 4 = 6

这就是本质不同的方案数

题目中已经保证给出所有置换中，只要加上一个不变的置换就能得到置换群

显然置换可以拆成多个轮换相乘

所以对每种轮换内的元素进行同种颜色的染色，那么轮换中的颜色经过此置换仍然不变

那么用一个01背包，就可以求出在一个置换下不变的元素个数

然后有模数，所以用逆元求一下分母

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 inline int Get()
 {
     int x = ;
     char c = getchar();
     while('' > c || c > '') c = getchar();
     while('' <= c && c <= '')
     {
         x = (x << ) + (x << ) + c - '';
         c = getchar();
     }
     return x;
 }
 const int me = ;
 int r, b, g, m, p, n, t;
 bool vis[me];
 int a[me];
 int si[me];
 int num;
 long long ans;
 long long f[me][me][me];
 inline long long Pow(long long x, int y)
 {
     long long res = ;
     long long sum = x % p;
     while(y)
     {
         if(y & ) res = (res * sum) % p;
         sum = (sum * sum) % p;
         y >>= ;
     }
     return res;
 }
 int main()
 {
     r = Get(), b = Get(), g = Get(), m = Get(), p = Get();
     n = r + b + g;
     ++m;
     t = m;
     while(m--)
     {
         num = ;
         memset(f, , sizeof(f));
         memset(si, , sizeof(si));
         memset(vis, false, sizeof(vis));
         for(int i = ; i <= n; ++i)
         {
             if(m) a[i] = Get();
             else a[i] = i;
         }
         for(int i = ; i <= n; ++i)
         {
             if(!vis[i])
             {
                 int c = a[i];
                 ++num;
                 while(!vis[c])
                 {
                     vis[c] = true;
                     ++si[num];
                     c = a[c];
                 }
             }
         }
         f[][][] = ;
         for(int i = ; i <= num; ++i)
             for(int j = r; j >= ; --j)
                 for(int k = b; k >= ; --k)
                     for(int l = g; l >= ; --l)
                     {
                         if(j >= si[i]) f[j][k][l] = (f[j][k][l] + f[j - si[i]][k][l]) % p;
                         if(k >= si[i]) f[j][k][l] = (f[j][k][l] + f[j][k - si[i]][l]) % p;
                         if(l >= si[i]) f[j][k][l] = (f[j][k][l] + f[j][k][l - si[i]]) % p;
                     }
         ans = (ans + f[r][b][g]) % p;
     }
     printf("%lld", (ans * Pow(t, p - )) % p);
 }