【2018.10.2】Note of CXM

1.有一张无向图，现在要给每个点染上黑色或白色，最后每个点的染色代价是它与离这个点最近的不同色节点的距离。求最小代价。所有边权$\geq 0$且互不相同。

分三种情况：

两点都染了色：两点都跟其它点算过最小距离了，不用管。

一点染了色：相当于扩展连通块，染了色的点向没染色的点扩展染色，颜色相同。

两点都没染色：两点直接相连（且边长是最短距离）。

2.题目大意同上，求得到最小代价的方案数。

0的边两边的点有多少个子树，方案数就累加上2的多少次方。

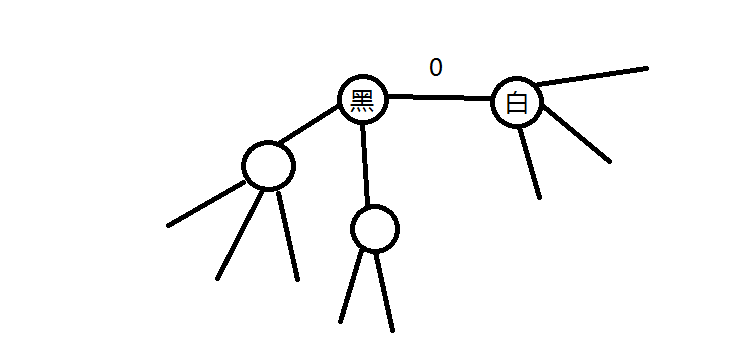
3.一张无向图，给每条边染两种颜色之一，使每个度大于等于2的点都连接两种颜色的边。问能否做到。Yes或No。

首先光秃秃的偶环（奇数条边）肯定无解（发芽就有解了），光秃秃的奇环（偶数条边）肯定有解（不知道这个结论的可以跳过这题了）。

环？想到了树。

可以先把这张图取出$n-1$条边，让整张图构成一棵树，

我们知道，树中只有三种边：树边（图中黑边）、回边（返祖边）（图中红边）、跨边（有向图特有）。

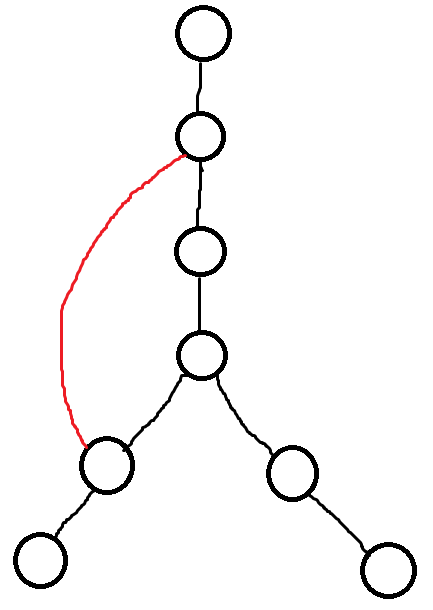
对于树上任意的度$\ge 2$ 的点，它的两边染上不同的颜色即可，如果再有一条返祖边连向它，这条新边染什么颜色都可以，必定能满足另一头的要求。

但对于度为 $1$ 的点呢？根和叶子结点都是度为1的点，这时候我们就要跑这个环。

只有这个环本身（即不算发芽）有偶数个点且发芽的情况需要我们考虑是否有解。

其实这就是偶环上发芽的情况。如图

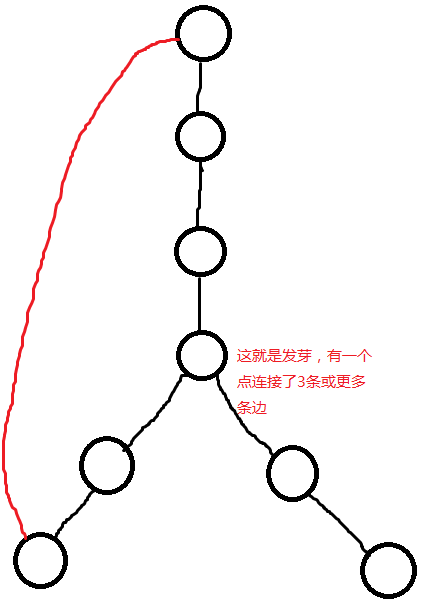
那么发芽点在原环上的两条相邻边就可以染成同色，然后把另一种颜色染到芽上。

但如果发的芽下面也有边连向了入读为1的边呢？

如果新连出来的环还是偶环，好像依然不可行。

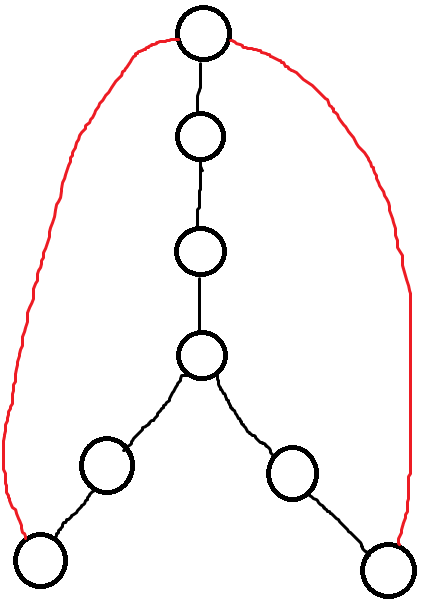
那什么情况下可行？如下。

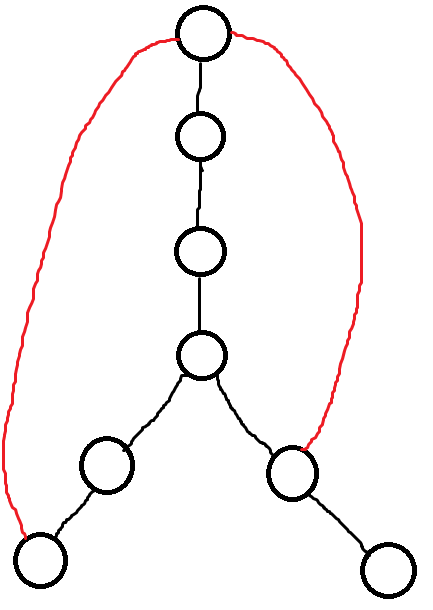
只要偶环与奇环相套，至少就可以从发芽点把另一种颜色沿着芽流出去了。

结合这么一个知识：偶环套偶环=偶环

可得：只有整张图只要存在纯偶环（就是不与奇环相套的偶环）就无解，否则有解。

所以这是个结论题，以上都是推导，并非题解。

题解的话就再扯点没用的（找纯偶环的方法）：去掉奇度点（它们是整张图的芽，处于被动染色状态，环上芽才是主动），把图的剩余部分做Tarjan求无向图强连通分量（MD准确地说是边双连通分量）。在每一个分量中任选一个起点，看是否存在经过偶数条边回到起点的方案。如果存在，说明存在奇环，这个强连通分量满足条件。如果所有的强连通分量都满足条件，说明图中不存在纯偶环，有解。否则存在纯偶环，无解。

4.有向图，边权只有0和1，求单源最短路。（线性算法）

我们都知道，广搜时总是取出队列中的第一个数。求最短路情况下，为了让更新尽量有意义，我们当然希望先从队列中取出（目前更新的）到起点距离尽量小的，这样可以尽量多地更新它周围点的最短路。

然后这题边权只有0和1，我们甚至不用写单调队列，如果按照上述贪心取法，我们发现广搜队列中 前面一段的距离值 与 后面一段的距离值 的差值不超过1。

为什么呢？

因为我们要取出到起点距离尽量小的，所以总是会取距离值相对较小的。并且更新时边权只会是0或1。

结合数学归纳法可知，

一开始队列中只有起点，距离为0，队列中距离值的差为0。

然后更新了周围的点，有些点的距离值更新为0，有些点的距离值更新为1。

然后我们一直更新 距离值为0的点 的周围的点，直到队列中所有点的距离值都为1。

此时已经不存在未被更新过的到起点距离为0的点了（广搜常识）。

此时队列中所有点的距离值是1。

然后把1当成之前的0，接下来更新出的距离值2当成之前的1，就归纳为一样的步骤了。

由此证明这样做的广搜队列中 前面一段的距离值 与 后面一段的距离值 的差值不超过1。

然后边权还只有0和1，队列操作比较简单，把通过权值为0更新的点接到队头，通过权值为1更新的点放到队尾即可。队头的点的距离值就是相对较小的。

拓展：有向图，边权只有0~20，求单源最短路。

把队列分割成21个桶，每个桶依次存$x,x+1,...,x+20$这21个距离值。广搜时不停取第一个桶中的点，把被该点更新距离的点 放到对应距离值的桶里。如果第一个桶中没有点，就把所有桶存放的距离值上调至使第一个桶中有点。

易证点肯定有桶放。

5.每个点有一个（开采矿物的）费用，边权依然只有0和1，求分别开采每个点的矿物时的最小费用。

6.执行k个操作，每个操作连接两个点，问每个操作后图中有多少条割边。（LCT会超时）

边双连通（环）的情况下给图缩点，这个图会变成一个森林。森林之间的每条边都是一条割边。因此用两个并查集维护，一个维护每个连通块的点，另一个维护每个边双连通块的点。